
“二倍角的正弦、余弦、正切”教学设计 王金城叶志良 设计理念:根据皮亚杰的认知发展理论,在个体从出生到成熟的发展过程中,智力发展 可以分为具有不同的质的四个主要阶段:激活原有认知结构、构建新的认知结构、尝试新 的认知结构、发展新的认知结构。发展的各个阶段顺序是一致的,前一阶段总是达到后 阶段的前提。阶段的发展不是间断性的跳跃,而是逐渐、持续的变化。皮亚杰的认知发展 阶段论为发展性辅导中学生智力发展水平的评估和诊断,提供了重要的理论依据。 教学内容:《普通高中课程标准实验教科书(数学)》必修4(人教A版),第三章、 第一节、第145-148页。 “二倍角的正弦、余弦、正切”是在研究了两角和与差的三角函数的基础上研究具有 “二倍角”关系的正弦、余弦、正切公式,它既是两角和的正弦、余弦、正切公式的特殊 化,又为以后求三角函数值、化简和证明提供了非常有用的理论工具,通过对二倍角公式 的推导知道:二倍角公式的内涵是“揭示具有倍数关系的两个角的三角函数的运算规律” 通过推导还让学生了解高中数学中由“一般”到“特殊”的化归数学思想,因此这节课也 是培养学生运算和逻辑推理能力的重要内容,对培养学生的探索精神和创新能力都有重要 意义。 教学目标:根据新课程标准的要求、本节教材的特点和学生对三角函数的认知特点,我 们把本节课的教学目标确定为: 1、能从两角和的正弦、余弦、正切公式出发推导出二倍角的正弦、余弦、正切公式, 理解它们的内在联系,从中体会数学的化归思想和数学规律的发现过程。 2、掌握二倍角的正弦、余弦、正切公式,通过对二倍角公式的正用、逆用、变形使 用,提高三角变形的能力,以及应用转化、化归、换元等数学思想方法解决问题的能力。 3、通过一题多解、一题多变,激发学生的学习兴趣,培养学生的发散性思维、创 新意识和数学情感,提高数学素养。 学情分析:我们的学生从认知角度上看,己经比较熟练的掌握了两角和与差的三角函数 的基础上。从学习情感方面看,大部分学生愿意主动学习。从能力上看,学生主动学习能 力、探究的能力、较弱
“二倍角的正弦、余弦、正切”教学设计 王金城 叶志良 设计理念:根据皮亚杰的认知发展理论,在个体从出生到成熟的发展过程中,智力发展 可以分为具有不同的质的四个主要阶段:激活原有认知结构、构建新的认知结构、尝试新 的认知结构、发展新的认知结构。发展的各个阶段顺序是一致的,前一阶段总是达到后一 阶段的前提。阶段的发展不是间断性的跳跃,而是逐渐、持续的变化。皮亚杰的认知发展 阶段论为发展性辅导中学生智力发展水平的评估和诊断,提供了重要的理论依据。 教学内容:《普通高中课程标准实验教科书(数学)》必修 4(人教 A 版),第三章、 第一节、第 145-148 页。 “二倍角的正弦、余弦、正切”是在研究了两角和与差的三角函数的基础上研究具有 “二倍角”关系的正弦、余弦、正切公式,它既是两角和的正弦、余弦、正切公式的特殊 化,又为以后求三角函数值、化简和证明提供了非常有用的理论工具,通过对二倍角公式 的推导知道:二倍角公式的内涵是“揭示具有倍数关系的两个角的三角函数的运算规律”, 通过推导还让学生了解高中数学中由“一般”到“特殊”的化归数学思想,因此这节课也 是培养学生运算和逻辑推理能力的重要内容,对培养学生的探索精神和创新能力都有重要 意义。 教学目标:根据新课程标准的要求、本节教材的特点和学生对三角函数的认知特点,我 们把本节课的教学目标确定为: 1、能从两角和的正弦、余弦、正切公式出发推导出二倍角的正弦、余弦、正切公式, 理解它们的内在联系,从中体会数学的化归思想和数学规律的发现过程。 2、掌握二倍角的正弦、余弦、正切公式,通过对二倍角公式的正用、逆用、变形使 用,提高三角变形的能力,以及应用转化、化归、换元等数学思想方法解决问题的能力。 3、通过一题多解、一题多变,激发学生的学习兴趣,培养学生的发散性思维、创 新意识和数学情感,提高数学素养。 学情分析:我们的学生从认知角度上看,已经比较熟练的掌握了两角和与差的三角函数 的基础上。从学习情感方面看,大部分学生愿意主动学习。从能力上看,学生主动学习能 力、探究的能力、较弱

教材分析:对公式的引入改变了教材中直接填结果的做法,而是通过提出问题,设置情 景对和角公式中的角&、日的关系特殊情形:=日时的简化,让学生探时发现、推证得 出二倍角公式,这样学生会感到自然,好接受,并可清晰知道和角的三角函数与二倍角公 式的联系,同时让学生学会怎样发现数学规律,并体会到化归(这里是将一般化归到特殊) 这一基本数学思想在发现中所起的作用,对教材的例题则有所增减,处理方式也有适当改 变。 教学重点、难点 重点:使学生在掌握了和角、差角公式后如何将和角公式化为二倍角公式,以及公式 的两种变形和公式成立的条件:如何学会去发现数学规律,并体会化归、转化等基本数学 思想在发现中所起的作用,能正确应用这些公式进行三角化简、求值、证明等。 难点:灵活应用二倍角公式变形的态式,熟练解三角综合题 教学过程 一、复习启发、设置情景、引出正题 1、(复习性提问):请同学回顾两角和的公式 (学生回答,教师板书) sin(a+8)=sin a cosB+cosasin 8 cos(a+B)=cosa cosB-sinasin B tna+=ma+tan日 1-tan atan B 2、(探索性提问)当上述公式中角&、P具有特殊化关系=日时,公式变为什么 形式?请一名学生到黑板上演示简化,其他同学在座位上做。 学生板书:
教材分析:对公式的引入改变了教材中直接填结果的做法,而是通过提出问题,设置情 景对和角公式中的角 、 的关系特殊情形 时的简化,让学生探讨发现、推证得 出二倍角公式,这样学生会感到自然,好接受,并可清晰知道和角的三角函数与二倍角公 式的联系,同时让学生学会怎样发现数学规律,并体会到化归(这里是将一般化归到特殊) 这一基本数学思想在发现中所起的作用,对教材的例题则有所增减,处理方式也有适当改 变。 教学重点、难点 重点:使学生在掌握了和角、差角公式后如何将和角公式化为二倍角公式,以及公式 的两种变形和公式成立的条件;如何学会去发现数学规律,并体会化归、转化等基本数学 思想在发现中所起的作用,能正确应用这些公式进行三角化简、求值、证明等。 难点:灵活应用二倍角公式变形的态式,熟练解三角综合题。 教学过程 一、复习启发、设置情景、引出正题 1、(复习性提问):请同学回顾两角和的公式 (学生回答,教师板书) 2、(探索性提问)当上述公式中角 、 具有特殊化关系 时,公式变为什么 形式?请一名学生到黑板上演示简化,其他同学在座位上做。 学生板书:

sin(a+a)sin acosa+cos asin a=sin 2a=2sin acos a cos(a+a)=cos acosa-sin asin a=cos2a=cos'a-sin2a m(c+a=a+nm2a= 2tan a 1-tan atan a 1-tan2 a 3、集体订正后,引导学生观察其结构,并指名回答观察结果 (学生回答:左边角均为2C,右边角均为“,具有“二倍”关系) 4、引入正题 师:肯定学生观察结论准确,并加以说明公式中蕴含着“对称”、“和谐”之美 教师板书(放幻灯片) sin 2a=2sin acos B cos 2a=cos2 a-sima →S2. tan 2c=1-tan c 2tan a →C2a 二倍角公式简记为了T:。 即为我们今天要学习的二倍角公式 【设计意图:复习已学公式,对其特殊化。让学生学会从“一般”到“特殊”的化归方 法,从而达到“温故知新”的教学目的】 二、引导探究、深化认识 1、回忆推导过程,让学生明确二倍角公式是和角公式的特殊情形。知道二者之间的联 系 2、(探索性提问)对C:
3、集体订正后,引导学生观察其结构,并指名回答观察结果 (学生回答:左边角均为 ,右边角均为 ,具有“二倍”关系) 4、引入正题 师:肯定学生观察结论准确,并加以说明公式中蕴含着“对称”、“和谐”之美 教师板书(放幻灯片) 二倍角公式简记为 即为我们今天要学习的二倍角公式 【设计意图:复习已学公式,对其特殊化。让学生学会从“一般”到“特殊”的化归方 法,从而达到“温故知新”的教学目的】 二、引导探究、深化认识 1、回忆推导过程,让学生明确二倍角公式是和角公式的特殊情形。知道二者之间的联 系 2、(探索性提问)对 :

cos2&=c0s2Q-m2&中的平方联想到m2&+cos2&=1,C2。有无其他变式2 (学生探索、总结得出两种变式:c0e2a=2c0s2c-1.c0s2c=1-2m2a) 3、(深化性提问):有了这组二倍角公式,我们是否可以放心大胆的应用呢? (学生:不能,要注意公式成立的条件) 引导学生联想和角公式的条件,利用类比的方法,探索出二倍角公式的条件 Sa sin 2a 2sinacos B(aER) Caa :cos2a=cos a-sina(aeR) 指出:尤其注意22成立的条件 【设计意图:引导学生应用联想、类比的教学思想、得出公式成立的条件】 4(棵案惟提月在中,当左边的8=分+女后 时,虽然右边的tn&不 存在,但左边的tam2c存在,能否用22求tan2a?该怎样求? tam2a=tam2g+k=tam(r+km)=tan开=0 引导学生:改用诱导公式: 2 【设计意图:引导学生对特殊情形,另辟溪径,寻找求解依据,培养学生细致、灵活 的探素习惯】
中的平方联想到 , 有无其他变式? (学生探索、总结得出两种变式: ) 3、(深化性提问):有了这组二倍角公式,我们是否可以放心大胆的应用呢? (学生:不能,要注意公式成立的条件) 引导学生联想和角公式的条件,利用类比的方法,探索出二倍角公式的条件 指出:尤其注意 成立的条件 【设计意图:引导学生应用联想、类比的教学思想、得出公式成立的条件】 4、(探索性提问)在 中,当左边的 时,虽然右边的 不 存在,但左边的 存在,能否用 求 ?该怎样求? 引导学生:改用诱导公式: 【设计意图:引导学生对特殊情形,另辟蹊径,寻找求解依据,培养学生细致、灵活 的探索习惯】

5、二倍角公式中的倍数关系是相对的,为深化对二倍角公式的理解,出示一组填空题 (放幻灯片) (1)填角 sin a=2sin cos corcom20g 号 co8=6o82_-m1 (2)(填=或≠号) -般情况下:$m2a_2 imn .cos2a_2cosg,tam2e_2tamd 【设计意图:通过填空,让学生灵活理解“二倍角”的含义,根据学生易混点,类比 公式,展开训练,达到“跨越障碍、突破难点”之目的】 三、巩固公式,学习应用 出示四道例题,学生分组训练,每组一题,做完后组内交流,订正答案,最后教师引 导学生小结方法、技巧、要点、解题规范等。 一放幻灯片 (第一组学生做)例1、不查表,求下列函数值
5、二倍角公式中的倍数关系是相对的,为深化对二倍角公式的理解,出示一组填空题 (放幻灯片) (1)填角 (2)(填 号) 一般情况下: 【设计意图:通过填空,让学生灵活理解“二倍角”的含义,根据学生易混点,类比 公式,展开训练,达到“跨越障碍、突破难点”之目的】 三、巩固公式,学习应用 出示四道例题,学生分组训练,每组一题,做完后组内交流,订正答案,最后教师引 导学生小结方法、技巧、要点、解题规范等。————放幻灯片 (第一组学生做)例 1、不查表,求下列函数值

(1)1n6730cos6730 ②co晋n 他 (4)sin 15 cos15 (51-28m225n 6 (6 1 6 【设计意图:通过直接应用公式、间接应用公式、一题多解,巩固二倍角公式】 ,求sim2acos2atan2a的值。 讲评:此题目中对角有范围限制,做题中应注意什么?仅知道1值,欲求二倍角正 弦、余弦、正切,先需要知道什么.在求c02a值时,要灵活应用C2。三种等价形式 并注意在求解过程中要尽量使用己知的原始数据,减少错误的可能性 【设计意图:由浅入深,巩固公式培养学生规范、科学解题的能力,教给学生小结解 题经验,做后反思】 1+sim48-cog48_1+n49+cog4 (第三组学生做)例3、证明 2tan0 1-tane 讲评:证法1:等价证: +0-c040-2in+c40 1-tam2日 1+sin48-cos482tam日 证法2:等价证:1+sin48+co84g1-tan'日 证法3:巧妙应用“1”,即用“1=n2日+co2日”代换,后略
【设计意图:通过直接应用公式、间接应用公式、一题多解,巩固二倍角公式】 (第二组学生做)例 2、已知 ,求 的值。 讲评:此题目中对角 有范围限制,做题中应注意什么?仅知道 值,欲求二倍角正 弦、余弦、正切,先需要知道什么?. .在求 值时,要灵活应用 三种等价形式, 并注意在求解过程中要尽量使用已知的原始数据,减少错误的可能性 【设计意图:由浅入深,巩固公式,培养学生规范、科学解题的能力,教给学生小结解 题经验,做后反思】 (第三组学生做)例 3、证明 讲评:证法 1:等价证: 证法 2:等价证: 证法 3:巧妙应用“1”,即用“ ”代换,后略

【设计意图:让学生学会等价证明、转化证题及一题多证,以培养学生数学思维的灵 活性、散发性及创造性思维,加深巩固二倍角公式和综合应用已学过的技巧证题】 (第四组学生做)例4、利用三角公式化简n50(1+V5tam10) 讲评:此题技巧是:先将“切化弦”,然后用已学过的知识和二倍角公式化简 【设计意图:复习应用所学知识解简单三角综合问题,培养学生综合解题应用能力】 四、提炼总结—放幻灯片 (1)在两角和的三角函数公式9C9了9中,当=户时,就可得到三 倍角的三角函数公式品。C。、7。说明:后者是前者的特例。 《2)马C。中角C没有条件限制,而了:中,只有 a:且a+ 时才成立。 (3)二倍角公式不仅限于2c是的二倍形式,其他如4a是2的二倍,2是4 的二倍,3是2的二倍等等都适用,要熟悉这些多形式的两个角的倍数关系,才能熟 练地应用好二倍角公式,这是灵活应用公式的关键。 c0s2a有三种形式cos2a=cos2a-1n2&=2cos2-1=1-2s1n2a.要依据 条件灵活应用公式,另外逆用此公式时更要注重结构形式
【设计意图:让学生学会等价证明、转化证题及一题多证,以培养学生数学思维的灵 活性、散发性及创造性思维,加深巩固二倍角公式和综合应用已学过的技巧证题】 (第四组学生做)例 4、利用三角公式化简 讲评:此题技巧是:先将“切化弦”,然后用已学过的知识和二倍角公式化简 【设计意图:复习应用所学知识解简单三角综合问题,培养学生综合解题应用能力】 四、提炼总结——放幻灯片 (1)在两角和的三角函数公式 中,当 时,就可得到二 倍角的三角函数公式 。说明:后者是前者的特例。 ( 2 ) 中 角 没有条件限制,而 中,只有 时才成立。 (3)二倍角公式不仅限于 是 的二倍形式,其他如 是 的二倍, 是 的二倍, 是 的二倍等等都适用,要熟悉这些多形式的两个角的倍数关系,才能熟 练地应用好二倍角公式,这是灵活应用公式的关键。 有三种形式: 。要依据 条件灵活应用公式,另外逆用此公式时更要注重结构形式

【设计意图:使学生对本节课所学知识的结构有一个清晰的认识,抓住重点、难点, 关健进行课后复习巩固】 五、作业布置 必做:教科书P150习题3.1A组14、15 【设计意图:培养学生自觉学习的习惯,检查学习效果,及时反馈,插漏补缺】 选做: (1)用sinc、cosc表示1n3a、cos3a(即推导三倍角公式) n牙0<x<牙求coe2x的值 (2)已知: c0s(+w 【设计意图:对学有余力的学生留出自我发展的空间,尝试能力,拓展创新】 设计思路: 1、本节公式比较多,首先要搞清楚各公式之间的内在联系,也就是要很好地理解上面 的知识结构图,其次理解如何由和角公式推导倍角公式,然后明确倍角的含义,熟练地运 用倍角公式进行求值、化简等三角运算及恒等变形。 2、在三角式的运算及恒等变形过程中,除了倍角公式外,也离不开前面所学的同角三 角函数关系、诱导公式以及和角公式等,它们是一个有机整体。在解题过程中要求学生先 分析条件与求解目标之间的差异,选择怡当的公式进行转化沟通,然后明确解题思路,设 计解题步骤,完善解答过程,培养逻辑思维能力。 3、我们通过一题多解,使我们学会数学思考与推理,训练发散性思维,培养创造新意 识,提高数学素养
【设计意图:使学生对本节课所学知识的结构有一个清晰的认识,抓住重点、难点, 关键进行课后复习巩固】 五、作业布置: 必做:教科书 P150 习题 3.1A 组 14、15 【设计意图:培养学生自觉学习的习惯,检查学习效果,及时反馈,插漏补缺】 选做: (1)用 、 表示 、 (即推导三倍角公式) (2)已知: 。 【设计意图:对学有余力的学生留出自我发展的空间,尝试能力,拓展创新】 设计思路: 1、本节公式比较多,首先要搞清楚各公式之间的内在联系,也就是要很好地理解上面 的知识结构图,其次理解如何由和角公式推导倍角公式,然后明确倍角的含义,熟练地运 用倍角公式进行求值、化简等三角运算及恒等变形。 2、在三角式的运算及恒等变形过程中,除了倍角公式外,也离不开前面所学的同角三 角函数关系、诱导公式以及和角公式等,它们是一个有机整体。在解题过程中要求学生先 分析条件与求解目标之间的差异,选择恰当的公式进行转化沟通,然后明确解题思路,设 计解题步骤,完善解答过程,培养逻辑思维能力。 3、我们通过一题多解,使我们学会数学思考与推理,训练发散性思维,培养创造新意 识,提高数学素养
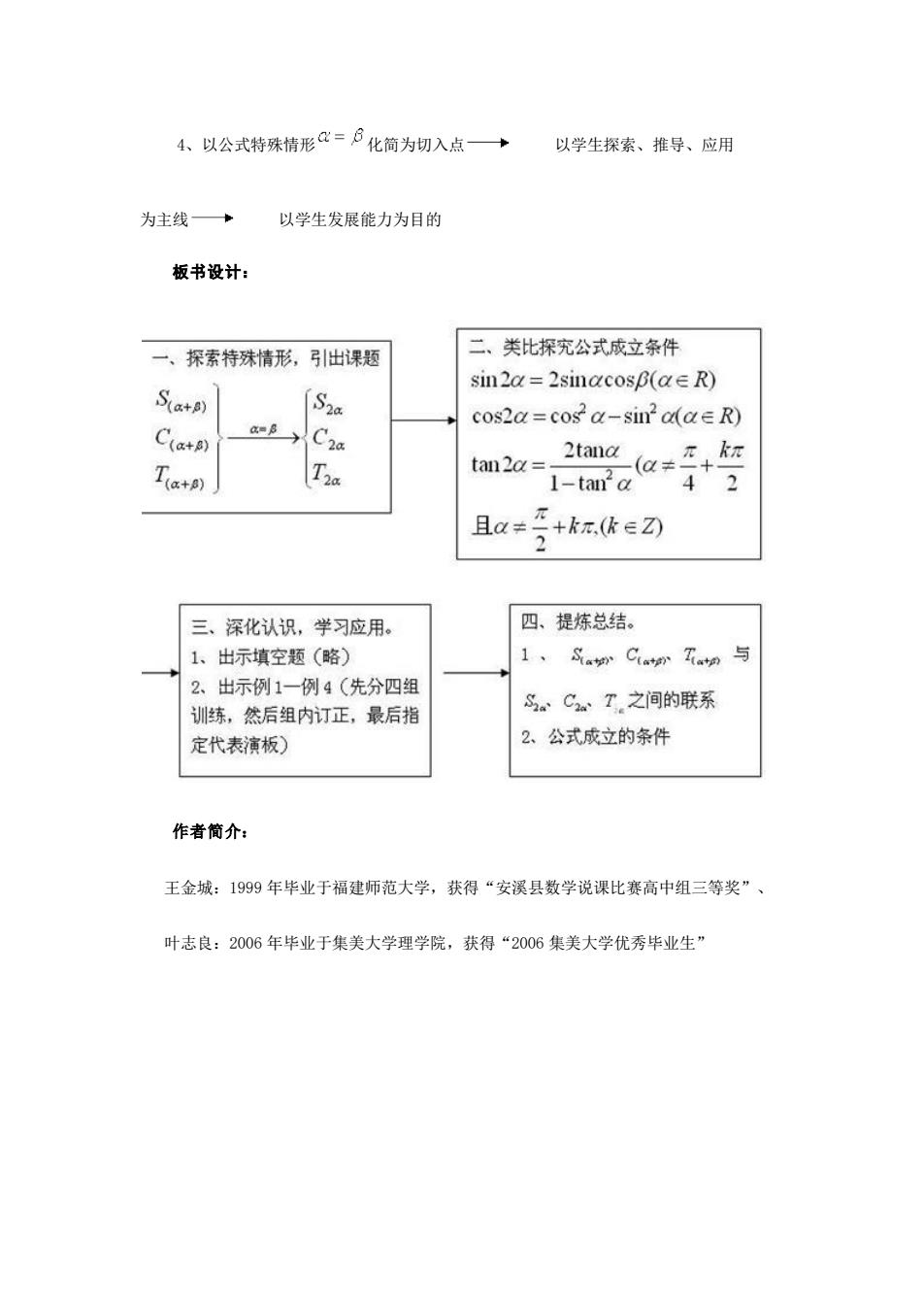
4、以公式特殊情形=户化简为切入点→ 以学生探索、推导、应用 为主线→ 以学生发展能力为目的 板书设计: 一、探索特殊情形,引出课题 二、类比探究公式成立条件 sin2a =2sinacosB(aE R) S(a+p) cos2a=cos a-sin'a(ae R) C(a+) aB C2a T2a tan2a= a导+号 且a≠ +k元.(keZ) 2 三、深化认识,学习应用。 四、提炼总结。 1、出示填空题(略) 1,。CmT与 2、出示例1一例4(先分四组 训练,然后组内订正,最后指 。C、T,之间的联系 定代表演板) 2、公式成立的条件 作者简介: 王金城:1999年毕业于福建师范大学,获得“安溪县数学说课比赛高中组三等奖”、 叶志良:2006年毕业于集美大学理学院,获得“2006集美大学优秀毕业生
4、以公式特殊情形 化简为切入点 以学生探索、推导、应用 为主线 以学生发展能力为目的 板书设计: 作者简介: 王金城:1999 年毕业于福建师范大学,获得“安溪县数学说课比赛高中组三等奖”、 叶志良:2006 年毕业于集美大学理学院,获得“2006 集美大学优秀毕业生