
基本不等式(第一课时) 陈永平 一.教学目标 知识目标:掌握两个正数的几何平均数不大于它们的算术平均数的定理,初 步学会运用定理解题 能力目标:培养学生观察、试验、归纳、判断、猜想等思维能力。 情感目标:培养学生严谨求实的科学态度,体会数与形的和谐统一,领略数 学的应用价值,激发学生的学习兴趣。 二,重点难点 重点:几何平均数不大于它们的算术平均数的定理: 难点:基本不等式的内涵及几何意义的挖掘。 三.教学过程 (1)创设意境,提出问题。 有一架天平两臂之长略有差异,其它均精确,小王要用它来称一物体的重 量,将此物体放在左右两个托盘各称一次,再将称的的数据相加后,除以2所
基本不等式(第一课时) 陈永平 一. 教学目标 知识目标:掌握两个正数的几何平均数不大于它们的算术平均数的定理,初 步学会运用定理解题. 能力目标:培养学生观察、试验、归纳、判断、猜想等思维能力。 情感目标:培养学生严谨求实的科学态度,体会数与形的和谐统一,领略数 学的应用价值,激发学生的学习兴趣。 二.重点难点 重点:几何平均数不大于它们的算术平均数的定理; 难点:基本不等式的内涵及几何意义的挖掘. 三.教学过程 (1)创设意境,提出问题。 有一架天平两臂之长略有差异,其它均精确,小王要用它来称一物体的重 量,将此物体放在左右两个托盘各称一次,再将称的的数据相加后,除以 2 所

得的结果就认为是物体的真实重量,你认为小王所测量结果是否准确?如果不 准确,比真实重量是重还是轻?你能给小王提供一种用这架天平称量此物体真 实重量的方法吗? (2)逐步分析,引入课题。 ①设第一次称量时,放物体一边的臂长为,另一边的臂长为?,称得物体 的重量为4,第二次称得物体的重量为b,用小王的方法所得的结果为 G'=a+6 2 ②探求真实重量G 4G=a① 1,G=地② ①×②得4G=ab G=品
得的结果就认为是物体的真实重量,你认为小王所测量结果是否准确?如果不 准确,比真实重量是重还是轻?你能给小王提供一种用这架天平称量此物体真 实重量的方法吗? (2)逐步分析,引入课题。 ①设第一次称量时,放物体一边的臂长为 ,另一边的臂长为 ,称得物体 的重量为 ,第二次称得物体的重量为 b,用小王的方法所得的结果为 ②探求真实重量 G ① ② ① ②得
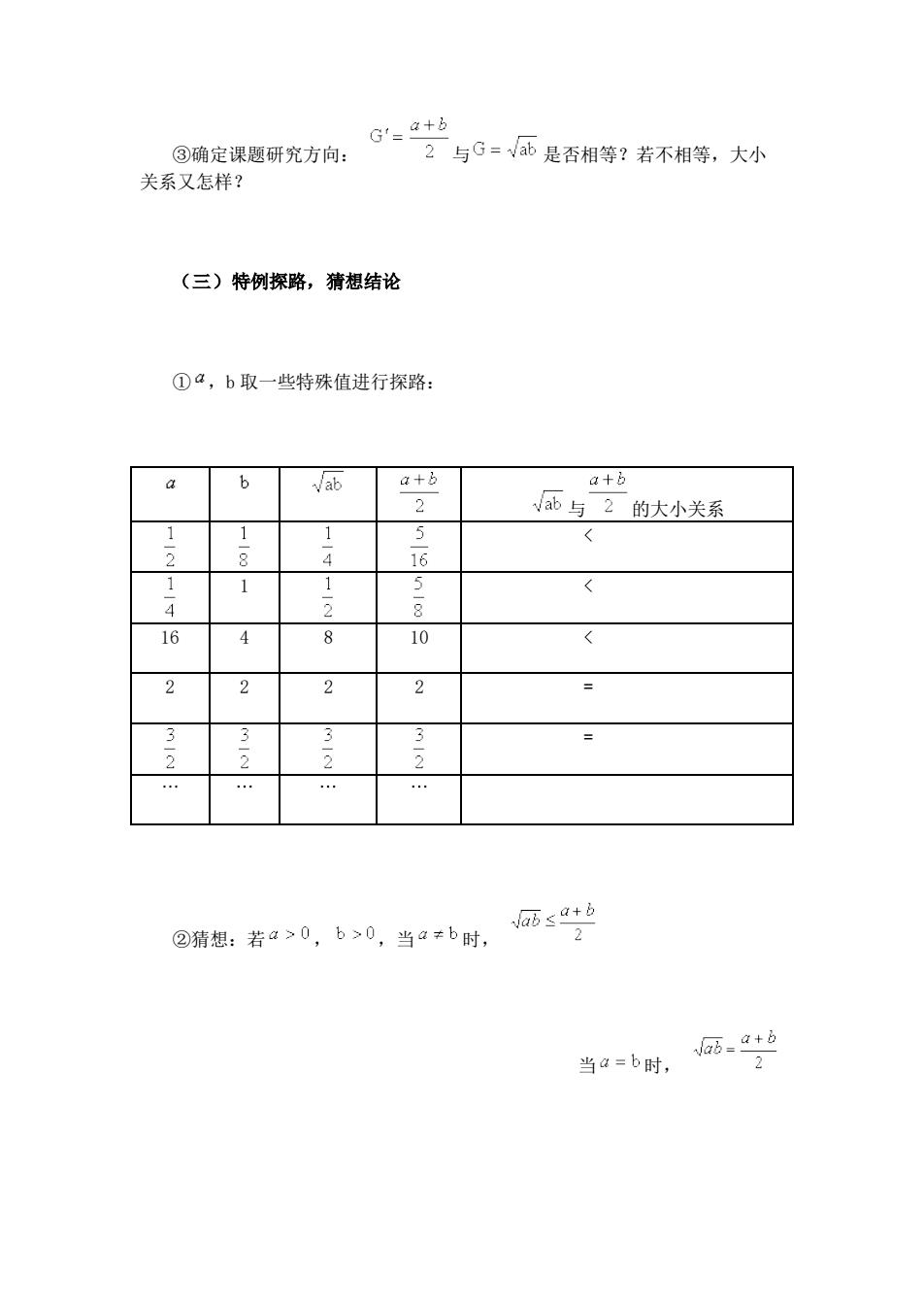
Gr=+6 ③确定课题研究方向: 2与G=而是否相等?若不相等,大小 关系又怎样? (三)特例探路,猜想结论 ①4,b取一些特殊值进行探路: b a+b √品与2的大小关系 r 4 16 8 10 2 ②猜想:若a>0,b>0,当a¥b时, 师生 当a=b时,+白
③确定课题研究方向: 与 是否相等?若不相等,大小 关系又怎样? (三)特例探路,猜想结论 ① ,b 取一些特殊值进行探路: 与 的大小关系 < 1 < 16 4 8 10 < 2 2 2 2 = = ②猜想:若 , ,当 时, 当 时

当ac0,b0,b>0时, a+b-历-a3+62-2画-6-620 2 2 (俏且收当=时生华 成立) 另外用公分别代替a,6
当 , 时,很明显 当 时, 无意义。 ③初步结论:如果 ,那么 成立。 (诱发学生深入思考问题,教会学习、研究的方法-从特殊到一般是科 学探求未知的有效手段。) (4)推证猜想,形成结论 ①提问:如何证明上述结论呢? 证明: , 时, (当且仅当 时 成立) 另外用 分别代替

又有a2+82-2ab=a-b奶20当a≠b时,a-2>0 当a=b时,(a-)2=0 a2+222ab(当且仅当a=b时“=”成立) ②得出结论: 林不特就海果是王数。事么压学(省发当时皮 立) 一般的:如果a,beR,那么a2+b222ab(当且仅当a=b时“=”成立) (5)挖据内涵,深化认识 atb ①称Vab为a,b的几何平均数:称2为a,b的算术平均数
又有 当 时, 当 时, (当且仅当 时“=”成立) ②得出结论: 基本不等式:如果 是正数,那么 (当且仅当 时“=”成 立) 一般的:如果 ,那么 (当且仅当 时“=”成立) (5)挖掘内涵,深化认识 ①称 为 的几何平均数;称 为 的算术平均数

这一基本不等式又可叙述为:两个正数的几何平均数不大于它们的算术 平均数 a+色2Na ②2 成立的条件仅需a20,6≥0就可以,但a=0或6=0时定理 显然成立,所以一般仅考察a>0,6>0的情况。 ③a2+b222ab成立的条件为a,beR。 (6)数形结合,相见益彰 ①附于6品s+ 2(a>0,6>0)的几何解释: 如图的圆0中:AB为圆的直径,AC=a,BC=b, 由射影定理:CD=ACCB,:CD=ACC8=Vb
这一基本不等式又可叙述为:两个正数的几何平均数不大于它们的算术 平均数 ② 成立的条件仅需 就可以,但 或 时定理 显然成立,所以一般仅考察 的情况。 ③ 成立的条件为 。 (6)数形结合,相见益彰 ①对于 ( )的几何解释: 如图的圆 O 中:AB 为圆的直径,AC= ,BC= , 由射影定理: , c

则弦DD'=2西,而直径A5≥弦DD',所以4+b≥2a西 当点C与圆心0重合时,即a=b时,等号成立。 (抓住时机,渗透数形结合思想,引导学生善于捕捉的暗示信息,从多方 位、多角度去理解并掌握所学知识,提升思维的灵活性) (7)适当引导,探索拓展 在基本不等式几何解释的基础上,运用几何画板,引导学生《+b是定值, 求ab最大值:b是定值,求a+b最小值的几何解释(由学生自己探索推导, 不但可使他们加深基本不等式的理解,还锻炼了他们的思维,培养了勇于探索 的精神) (8)例题示范,学会应用 例1:已知=1且x>0,y>0,求x+y的最小值。 支式0D:求话数中红>0的最小信
则弦 ,而直径 弦 ,所以 当点 C 与圆心 O 重合时,即 时,等号成立。 (抓住时机,渗透数形结合思想,引导学生善于捕捉的暗示信息,从多方 位、多角度去理解并掌握所学知识,提升思维的灵活性) (7)适当引导,探索拓展 在基本不等式几何解释的基础上,运用几何画板,引导学生 是定值, 求 最大值; 是定值,求 最小值的几何解释(由学生自己探索推导, 不但可使他们加深基本不等式的理解,还锻炼了他们的思维,培养了勇于探索 的精神) (8)例题示范,学会应用 例 1:已知 且 ,求 的最小值。 变式(1):求函数 的最小值

变式(2):求肠数”+G2,求函数”=x x-2的最小值。 1 变式:已知x>2,不等式十一2之“相成立,则实数“的范国 (题后小结:略) 练习()若x>0,=+ 的最值为此时x= (②)若x0,y>0且x+y=2,求0的最大值. 例2. 变式1:己知0<x<2,求函数y=x2-x的最大值. 变式2:已知0<x<号求函数y=x2-3x的最大值
变式(2):求函数 的最大值。 变式(3):已知 ,求函数 的最小值。 变式(4):已知 ,不等式 恒成立,则实数 的范围 _. (题后小结:略) 练习 (1)若 , 的最_值为_,此时 =_. (2)若 , 的最_值为_,此时 =_. 例 2

(题后小结:略) (让学生初步学会运用基本不等式并注意基本不等式适用范围及等号成立 的条件。) (9)归纳小结,反思提高 提问:①通过本节课的学习,你学到了什么知识? ②在解决问题的基础上,你掌握了哪些探求问题的方法和 数学思想方法? 在学生回答的基础上,再由教师进行补充规范。 (先由学生小结,再在不当之处由教师点评,有利于学生构建自己的知识体 系,形成知识的正向迁移) (10)布置作业,分层对待。 书面作业:P114习题3.4:A组1
(题后小结:略) (让学生初步学会运用基本不等式并注意基本不等式适用范围及等号成立 的条件。) (9)归纳小结,反思提高 提问:①通过本节课的学习,你学到了什么知识? ②在解决问题的基础上,你掌握了哪些探求问题的方法和 数学思想方法? 在学生回答的基础上,再由教师进行补充规范。 (先由学生小结,再在不当之处由教师点评,有利于学生构建自己的知识体 系,形成知识的正向迁移) (10)布置作业,分层对待。 书面作业:P114 习题 3.4:A 组 1

带性作:是活延有联他正明不号大历学(。>06>心和 a2+2≥2ab方法和几何解释? (作业分必做的书面作业和选做的弹性作业,弹性作业供学有余力的学生 思考,使他们有提高发展的空间)
弹性作业:是否还有其他证明不等式 ( )和 方法和几何解释? (作业分必做的书面作业和选做的弹性作业,弹性作业供学有余力的学生 思考,使他们有提高发展的空间)