
古曲幅型 琼海市嘉积中学赵亮 课愿 古典颜型 项目 容 理论依据或意图 本节课是高中数学3(必修)第三章概率的第二节古典概型的 女 第一课时,是在随机事件的概率之后,几何概型之前,尚未学习排 列组合的情况下教学的。古典概型是一种特殊的数学模型,也是 种最基本的概率模型,在率论中占有相当重要的地位。 及作 学好古典概型可以为其它概率的学习莫定基础,同时有利 兔 于理解概率的概念,有利于计算一些事件的概率,有利于解释生 中的一一些问题。 材 教学 根据本节课的地位利 理解古典概型的念及利用古典概型求解随机事件的概率, 作用以及新课程标准的具 套 体要求,制订教学重点。 根据本节课的内容, 如何判新一个试验是否是古典概型,分清在一个古具概型中 即尚未学习排列组合,以及 难点 某随机事件包含的基本事件的个数和试验中基本事件的总数。 学生的心理特点和认知水 制定了教学难点。 分
古典概型 琼海市嘉积中学 赵亮 课题 古典概型 项目 内 容 理论依据或意图 教 材 分 教 材 地 位 及 作 用 本节课是高中数学 3(必修)第三章概率的第二节古典概型的 第一课时,是在随机事件的概率之后,几何概型之前,尚未学习排 列组合的情况下教学的。古典概型是一种特殊的数学模型,也是一 种最基本的概率模型,在概率论中占有相当重要的地位。 学好古典概型可以为其它概率的学习奠定基础,同时有利 于理解概率的概念,有利于计算一些事件的概率,有利于解释生活 中的一些问题。 教 学 重 点 理解古典概型的概念及利用古典概型求解随机事件的概率。 根据本节课的地位和 作用以及新课程标准的具 体要求,制订教学重点。 教 学 难 点 如何判断一个试验是否是古典概型,分清在一个古典概型中 某随机事件包含的基本事件的个数和试验中基本事件的总数。 根据本节课的内容, 即尚未学习排列组合,以及 学生的心理特点和认知水 平,制定了教学难点

1.知识与技能 )理解古典概型及其概率计算公式, (2)会用列举法计算一些随机事件所含的基本事件数及事件发生的 奇 概率。 2.过程与方法 根据新课程标准,并 析 结合学生心理发展的需求, 根据本节课的内容和学生的实际水平,通过模拟试验让学生 理解古典概型的特征:试验结果的有限性和每一个试验结果出现的 以及人格、情感、价值观的 等可能性,观察类比各个试验,归纳总结出古典概型的概率计算公 具休塑求制订而成。这对器 式,体现了化归的重要思想,掌列举法,学会运用数形结合、分 发学生学好数学念 目 类讨论的思想解决概率的计算问愿。 数学习惯,感受数学思想 提高数学能力起到了积极 3。 情感态度与价值观 的作用。 概率教学的核心问题是让学生了解随机现象与概率的意义 加强与实际生活的联系,以科学的态度评价身边的一些随机现象 适当地增加学生合作学习交流的机会,尽量地让学生自己举出生语 和学习中与古奥概型有关的实例。使得学生在体会概率意义的同 时,感受与他人合作的重要性以及初步形成实事求是地科学态度不 锲而不舍的求学精神。 项目 容 师生活动理论依据或意
析 教 学 目 标 1.知识与技能 (1)理解古典概型及其概率计算公式, (2)会用列举法计算一些随机事件所含的基本事件数及事件发生的 概率。 2.过程与方法 根据本节课的内容和学生的实际水平,通过模拟试验让学生 理解古典概型的特征:试验结果的有限性和每一个试验结果出现的 等可能性,观察类比各个试验,归纳总结出古典概型的概率计算公 式,体现了化归的重要思想,掌握列举法,学会运用数形结合、分 类讨论的思想解决概率的计算问题。 3.情感态度与价值观 概率教学的核心问题是让学生了解随机现象与概率的意义, 加强与实际生活的联系,以科学的态度评价身边的一些随机现象。 适当地增加学生合作学习交流的机会,尽量地让学生自己举出生活 和学习中与古典概型有关的实例。使得学生在体会概率意义的同 时,感受与他人合作的重要性以及初步形成实事求是地科学态度和 锲而不舍的求学精神。 根据新课程标准,并 结合学生心理发展的需求, 以及人格、情感、价值观的 具体要求制订而成。这对激 发学生学好数学概念,养成 数学习惯,感受数学思想, 提高数学能力起到了积极 的作用。 项 目 内 容 师生活动 理论依据或意 图

在课前,教师布置任务,以数学小组为单位,完成下面两个模 拟试验, 试验一:抛掷一枚质地均匀的硬币,分别记录“正面朝上”利 “反面朝上”的次数,要求每个数学小组至少完成20次(最好是整 十数),最后由科代表汇总: 通过课前的模 拟实验的展 试验二:抛掷一枚质地均匀的酸子,分别记录“1点”、“2 的操作力 让学生感受与 点”、“3点”、“4点”、“5点”和“6点”的次数,要求每个 法和试给 他人合作的重 数学小组至少完成60次(最好是整十数),最后由科代表汇总 结果。并 顶性,培养学生 与同学 用学语 在课上,学生展示模拟试验的操作方法和试验结果,并与同学 提出 的能力。随着 交流活动感受。 受,教 问题的提出,斋 引入 最后汇总 发了学生的求 教师最后汇总方法、结果和感受,并提出问思? 方法,结 知欲锥,通过惠 断课 1.用模拟试验的方法来求某一随机事件的概率好不好?为什 果和感 察对比,培养了 么? 受,并提 学生发现问 出问题。 的能力。 不好,要求出某一随机事件的概率,需要进行大量的试验,并 且求出来的结果是率,而不是概率。 2.根据以前的学习,上述两个模拟试验的每个结果之都有什 么特点?
教 学 过 一 提出 问题 引入 新课 在课前,教师布置任务,以数学小组为单位,完成下面两个模 拟试验: 试验一:抛掷一枚质地均匀的硬币,分别记录“正面朝上”和 “反面朝上”的次数,要求每个数学小组至少完成 20 次(最好是整 十数),最后由科代表汇总; 试验二:抛掷一枚质地均匀的骰子,分别记录“1 点”、“2 点”、“3 点”、“4 点”、“5 点”和“6 点”的次数,要求每个 数学小组至少完成 60 次(最好是整十数),最后由科代表汇总。 在课上,学生展示模拟试验的操作方法和试验结果,并与同学 交流活动感受。 教师最后汇总方法、结果和感受,并提出问题? 1.用模拟试验的方法来求某一随机事件的概率好不好?为什 么? 不好,要求出某一随机事件的概率,需要进行大量的试验,并 且求出来的结果是频率,而不是概率。 2.根据以前的学习,上述两个模拟试验的每个结果之间都有什 么特点? 学生展示 模拟试验 的操作方 法和试验 结果,并 与同学交 流活动感 受,教师 最后汇总 方法、结 果和感 受,并提 出问题。 通过课前的模 拟实验的展示, 让学生感受与 他人合作的重 要性,培养学生 运用数学语言 的能力。随着新 问题的提出,激 发了学生的求 知欲望,通过观 察对比,培养了 学生发现问题 的能力

程二 在试验一中随机事件只有两个,即“正面朝上”和“反面钥上”, 并且他们都是互斥的,由于硬币质地是均匀的,因此出现两种随机 1 事件的可能性相等,即它们的概率都是2, 在试验二中随机事件有六个,即“1点”、“2点”、“3点” “4点”、“5点”和“6点”,并且他们都是互斥的,由于骰子质 地是均匀的,因此出现六种随机事件的可能性相等,即它们的概率 让学生从问题 学生观家 的相同点和不 都是6. 司点中找出母 对比得 两个模 象的 我们把上述试验中的随机事件称为基本事件,它是试验的每 试验的相 一面,这能封 养学生分析问 个可能结果。 同点和不 题的能力.同 同点。教 析 也教会学生运 基本事件有如下的两个特点: 师给出基 本事件的 (1)任何两个基本事件是互斥的 概念, 辩证唯物主义 观点来分析问 对相关特 (2)任何率件(除不可能事件)都可以表示成基本件的和 点加以说 腿的一种方法。 明.加 特点(2)的理解:在试验一中,必然事件由基本事件“正面朝 教师的注解可 新概念的 上”和“反面朝上”组成:在试验二中,随机事件“出现偶数点” 以使学牛中好 理解 可以由基本事件“2点”、“4点”和“6点”共同组成。 的把握问的 关键。 项目 内 师生活动理论依据或意 图 先让学 例1从字母a,立,c,心中任意取出两个不同字母的试验中,有事些基 数形结合和 尝试着列 分类讨论的思 本事件? 出所有的 想渗透到具体 基本事 同题中来。由习 分析:为了解基本事件,我们可以按照字典排序的顺序,把所有可 沿右学习排列 能的结果都列出来。利用树状图可以将它们之间的关系列出来。 再讲解用 组合,因此用列 树状图列 举法列举基 我们一般用列举法列出所有基本事件的结果。画树状图是列端 举问题的 事件的个数,不 法的本方法, 一般分布完成的结果(两步以上)可以用树状图进行 仅能让学生直
程 分 析 二 思 考 交 流 形 成 概 念 在试验一中随机事件只有两个,即“正面朝上”和“反面朝上”, 并且他们都是互斥的,由于硬币质地是均匀的,因此出现两种随机 事件的可能性相等,即它们的概率都是 ; 在试验二中随机事件有六个,即“1 点”、“2 点”、“3 点”、 “4 点”、“5 点”和“6 点”,并且他们都是互斥的,由于骰子质 地是均匀的,因此出现六种随机事件的可能性相等,即它们的概率 都是 。 我们把上述试验中的随机事件称为基本事件,它是试验的每一 个可能结果。 基本事件有如下的两个特点: (1)任何两个基本事件是互斥的; (2)任何事件(除不可能事件)都可以表示成基本事件的和。 特点(2)的理解:在试验一中,必然事件由基本事件“正面朝 上”和“反面朝上”组成;在试验二中,随机事件“出现偶数点” 可以由基本事件“2 点”、“4 点”和“6 点”共同组成。 学生观察 对比得出 两个模拟 试验的相 同点和不 同点,教 师给出基 本事件的 概念,并 对相关特 点加以说 明,加深 新概念的 理解。 让学生从问题 的相同点和不 同点中找出研 究对象的对立 统一面,这能培 养学生分析问 题的能力,同时 也教会学生运 用对立统一的 辩证唯物主义 观点来分析问 题的一种方法。 教师的注解可 以使学生更好 的把握问题的 关键。 项 目 内 容 师生活动 理论依据或意 图 教 二 思 例 1 从字母 中任意取出两个不同字母的试验中,有哪些基 本事件? 分析:为了解基本事件,我们可以按照字典排序的顺序,把所有可 能的结果都列出来。利用树状图可以将它们之间的关系列出来。 我们一般用列举法列出所有基本事件的结果,画树状图是列举 法的基本方法,一般分布完成的结果(两步以上)可以用树状图进行 先让学生 尝试着列 出所有的 基本事 件,教师 再讲解用 树状图列 举问题的 将数形结合和 分类讨论的思 想渗透到具体 问题中来。由于 没有学习排列 组合,因此用列 举法列举基本 事件的个数,不 仅能让学生直
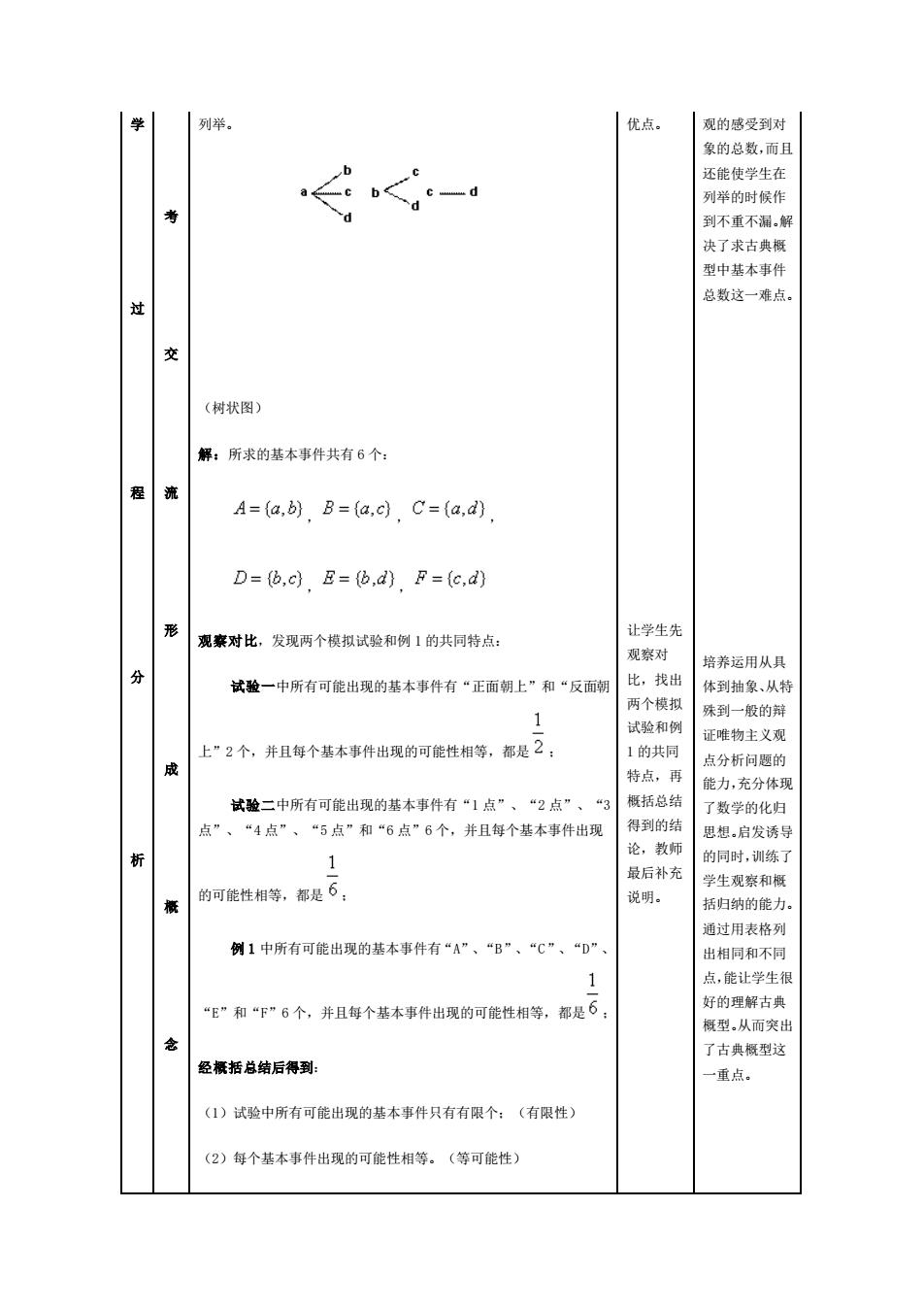
列举 优点。 观的感受到对 单的总数.面 还能使学生有 列举的时候作 到不重不漏.解 决了求古典辉 型中基本事件 总数这 一难点 (树状图) 解:所求的基本事件共有6个: A=(a,b)B=(a,c)C=(a,d) D=他,c)E=6,d)F=c,d) 观察对比,发现两个模拟试验和例1的共同特点: 让学生先 观察对 培养运用从 试验一中所有可能出现的基本事件有“正面朝上”和“反面蓟 比,找出 体到抽象、从特 两个模扣 试验和例 殊到一般的辩 1 证唯物主义观 上“2个,并且每个基本事件出现的可能性相等,都是2】 1的共同 与公折问厦的 特点。再 能力,充分体现 试验二中所有可能出现的基本事件有“1点”、“2点”、 概括总结 了数学的化归 点”、“4点”、“5点”和“6点”6个,并且每个基本事件出现 得到的名 思想启发诱导 析 ,教师 的园时,练了 1 最后补充 学生理容和相 的可能性相等,都是6 说明。 括归纳的能力 通过用表格列 例1中所有可能出现的基本事件有“A”、“B“、“C”、“D” 出相同和不同 1 点,能让学生很 “E”和“F”6个,并且每个基本事件出现的可能性相等,都是6 好的理解古典 了古典概型这 经概括总结后得到: 重点。 (1)试验中所有可能出现的基本事件只有有限个:(有限性) (2)每个基本事件出现的可能性相等。(等可能性)
学 过 程 分 析 考 交 流 形 成 概 念 列举。 (树状图) 解:所求的基本事件共有 6 个: , , , , , 观察对比,发现两个模拟试验和例 1 的共同特点: 试验一中所有可能出现的基本事件有“正面朝上”和“反面朝 上”2 个,并且每个基本事件出现的可能性相等,都是 ; 试验二中所有可能出现的基本事件有“1 点”、“2 点”、“3 点”、“4 点”、“5 点”和“6 点”6 个,并且每个基本事件出现 的可能性相等,都是 ; 例 1 中所有可能出现的基本事件有“A”、“B”、“C”、“D”、 “E”和“F”6 个,并且每个基本事件出现的可能性相等,都是 ; 经概括总结后得到: (1)试验中所有可能出现的基本事件只有有限个;(有限性) (2)每个基本事件出现的可能性相等。(等可能性) 优点。 让学生先 观察对 比,找出 两个模拟 试验和例 1 的共同 特点,再 概括总结 得到的结 论,教师 最后补充 说明。 观的感受到对 象的总数,而且 还能使学生在 列举的时候作 到不重不漏。解 决了求古典概 型中基本事件 总数这一难点。 培养运用从具 体到抽象、从特 殊到一般的辩 证唯物主义观 点分析问题的 能力,充分体现 了数学的化归 思想。启发诱导 的同时,训练了 学生观察和概 括归纳的能力。 通过用表格列 出相同和不同 点,能让学生很 好的理解古典 概型。从而突出 了古典概型这 一重点

我们将具有这两个特点的概率模型称为古典震率摄型,简称古典橛 型 思考交流 (1)向一个圆面内随机地投射一个点,如果该点落在圆内任 一点都是等可能的,你认为这是古典概型吗?为什么? 学生互相 交流,回 答补充 教师归 纳。 两个问题的设 计是为了让党 生更加准确的 把握古典概型 的两个特点,穷 破了如何判断 一个试验是否 是古典概型这 一教学难点 项目 内 师生活动理论依据或意 图 答:不是古典概型,因为试验的所有可能结果是圆面内所有的 点,试验的所有可能结果数是无限的,国然每一个试验结果出现的 “可能性相同”,但这个试验不满足古典概型的第一个条件。 (2)如图,某同学随机地向一靶心进行射击,这一试验的结果 形 只有有限个:命中10环、命中9环.命中5环和不中环。你认为 这是古典概型吗?为什么? 成概 学 不是古典概型,因为试验的所有可能结果只有7个,而命中10 环、命中9环. .命中5环和不中环的出现不是等可能的,即不满 足古典概型的第二个条件
我们将具有这两个特点的概率模型称为古典概率概型,简称古典概 型。 思考交流: (1)向一个圆面内随机地投射一个点,如果该点落在圆内任意 一点都是等可能的,你认为这是古典概型吗?为什么? 学生互相 交流,回 答补充, 教师归 纳。 两个问题的设 计是为了让学 生更加准确的 把握古典概型 的两个特点。突 破了如何判断 一个试验是否 是古典概型这 一教学难点。 项 目 内 容 师生活动 理论依据或意 图 教 学 思 考 交 流 形 成 概 念 答:不是古典概型,因为试验的所有可能结果是圆面内所有的 点,试验的所有可能结果数是无限的,虽然每一个试验结果出现的 “可能性相同”,但这个试验不满足古典概型的第一个条件。 (2)如图,某同学随机地向一靶心进行射击,这一试验的结果 只有有限个:命中 10 环、命中 9 环.命中 5 环和不中环。你认为 这是古典概型吗?为什么? 答:不是古典概型,因为试验的所有可能结果只有 7 个,而命中 10 环、命中 9 环.命中 5 环和不中环的出现不是等可能的,即不满 足古典概型的第二个条件

向题思考:在古典概型下,基本事件出现的概率是多少?随机事件 教师提出鼓励学生运用 出现的概率如何计算? 题。引 观察类出和从 具体到抽 分析 比分析两 特殊到一般的 个模拟试 辩证唯物主义 实验一中,出现正面朝上的概率与反而朝上的概率相等,即 验和例1 方法来分析问 的概, 愿,同时让学 P(“正面朝上”)=P(“反而朝上”) 先通过用 受数学化归 概率加 息想的优越 由概率的加法公式,得 公式求出 和这一做法的 随机车件 合理性,突出了 P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1 的概率, 古典概型的概 再对比概 率计算公议 率结果, 重点。 因此P(“正面朝上”)=P(“反面糊上”)=2 发现其中 来 的联系. 男程有-宁生爱李热m边 试验 二中,出现各个点的概率相等,即 P(“1点”)=P(“2点”)=P(“3点”) =P(“4点”)=P(“5点”)=P(“6点”) 反复利用概率的加法公式,我们有 鞭 P(“1点”)+P(“2点”)+P(“3点”)+P(“4点”+ (“5点”)+P(“6点”)=P(必然事件)=1 析 所以P(“1点”)=P(“2点”)=P(“3点”) 1 =P(4点”)=P(“5点”)=P(“6点”)=6 方 进一步地,利用加法公式还可以计算这个试验中任何一个事件的概 米,例如, 程 P(“出现偶数点”)=P(“2点”)+P(“4点”)+P(“6点”) 11131 =6+6+6-6-2 根据
过 程 分 析 三 观 察 分 析 推 导 方 程 问题思考:在古典概型下,基本事件出现的概率是多少?随机事件 出现的概率如何计算? 分析: 实验一中,出现正面朝上的概率与反面朝上的概率相等,即 P(“正面朝上”)=P(“反面朝上”) 由概率的加法公式,得 P(“正面朝上”)+P(“反面朝上”)=P(必然事件)=1 因此 P(“正面朝上”)=P(“反面朝上”)= 即 试验 二中,出现各个点的概率相等,即 P(“1 点”)=P(“2 点”)=P(“3 点”) =P(“4 点”)=P(“5 点”)=P(“6 点”) 反复利用概率的加法公式,我们有 P(“1 点”)+P(“2 点”)+P(“3 点”)+P(“4 点”)+P (“5 点”)+P(“6 点”)=P(必然事件)=1 所以 P(“1 点”)=P(“2 点”)=P(“3 点”) =P(“4 点”)=P(“5 点”)=P(“6 点”)= 进一步地,利用加法公式还可以计算这个试验中任何一个事件的概 率,例如, P(“出现偶数点”)=P(“2 点”)+P(“4 点”)+P(“6 点”) = + + = = 即 根据 教师提出 问题,引 导学生类 比分析两 个模拟试 验和例 1 的概率, 先通过用 概率加法 公式求出 随机事件 的概率, 再对比概 率结果, 发现其中 的联系。 鼓励学生运用 观察类比和从 具体到抽象、从 特殊到一般的 辩证唯物主义 方法来分析问 题,同时让学生 感受数学化归 思想的优越性 和这一做法的 合理性,突出了 古典概型的概 率计算公式这 一重点

上述两则模拟试验,可以摄括总结出,古典极型计算任何事件的授 率计算公式为: 开A)=A所包含的基本事件的个数 基本事件的总数 项目 容 师生活动理论依据成意 图 提问: 教师提 深化对古典概 问,学生 的据率计 ()在例1的实验中,出现字母“”的概率是多少? 回答, 公式的理解,世 三 深对古典 抓住了解决古 出现字母“d”的概率为 概型的概 典概型的概率 率计算公 计算的关键, 式的理 学 来提问: 分(2)在使用古典概型的概率公式时,应该注意什么? 归钠: 推 在使用古典概型的概率公式时,应该注意。 过 导 (1)要判新该概率模型是不是古典概型: 方 (2)要找出随机事件A包含的基本事件的个数和试验中基本事件的 总数。 除了画树状图,还有什么方法求基本事件的个数呢?
上述两则模拟试验,可以概括总结出,古典概型计算任何事件的概 率计算公式为: 项 目 内 容 师生活动 理论依据或意 图 教 学 过 三 观 察 分 析 推 导 方 程 提问: (1)在例 1 的实验中,出现字母“d”的概率是多少? 出现字母“d”的概率为: 提问: (2)在使用古典概型的概率公式时,应该注意什么? 归纳: 在使用古典概型的概率公式时,应该注意: (1)要判断该概率模型是不是古典概型; (2)要找出随机事件 A 包含的基本事件的个数和试验中基本事件的 总数。 除了画树状图,还有什么方法求基本事件的个数呢? 教师提 问,学生 回答,加 深对古典 概型的概 率计算公 式的理 解。 深化对古典概 型的概率计算 公式的理解,也 抓住了解决古 典概型的概率 计算的关键

程四例2单选瑟是标准化考试中常用的题型,一般是从A,B,C,D四个 选项中选择一个正确答案。如果考生掌拆了考差的内容,他可以选 唯 一正确的答案。假设考生不会做,他随机的选择一个答案,问 他答对的概率是多少? 分析: 例 解决这个问圈的关健,即讨论这个问圈什么情况下可以看成古典概 型。如果考生掌岸或者掌提了部分考察内容。这都不满足古泉概型 的第2个性一 一等可能性,因此,只有在假定考生不会做。随机 地选择了 一个答案的情况下,才可以化为古奥概型 让学生明确决 解: 概率的计算问 题的关键是:先 这是一个古典概型,因为试验的可能结果只有4个:选择人、选择B、 学生先思 要判断该概率 选择C,选择D,即基本事件共有4个,考生随机地选择一个答案是 考再回 横型是不是古 析 选择A,B,C,D的可能性是相等的。从而由古臭概型的概率计算公 答,教师 典将型,再题找 对学生冯 析 式得: 出随机事件 有注意到 包含的基本 的关键点 件的个数和过 课后思 加以说 验中基本事件 明。 的总数。 (1)在标准化考试中既有单选题又有多进愿,多选题是从A,B, 明用学生对 C,D四个进项中透出所有正确的答案,同学们可能有一种感觉,如 学知识的掌提 果不知道正确答案, 多选题更难猜对,这是为什么? (②)假设有20道单选题,如果有一个考生答对了17道避,他是 随机选择的可能性大,还是他掌握了一定知识的可能性大? 项目 内 师生活动理论依据或意 图
程 分 析 四 例 题 分 析 推 广 应 用 例 2 单选题是标准化考试中常用的题型,一般是从 A,B,C,D 四个 选项中选择一个正确答案。如果考生掌握了考差的内容,他可以选 择唯一正确的答案。假设考生不会做,他随机的选择一个答案,问 他答对的概率是多少? 分析: 解决这个问题的关键,即讨论这个问题什么情况下可以看成古典概 型。如果考生掌握或者掌握了部分考察内容,这都不满足古典概型 的第 2 个条件——等可能性,因此,只有在假定考生不会做,随机 地选择了一个答案的情况下,才可以化为古典概型。 解: 这是一个古典概型,因为试验的可能结果只有 4 个:选择 A、选择 B、 选择 C、选择 D,即基本事件共有 4 个,考生随机地选择一个答案是 选择 A,B,C,D 的可能性是相等的。从而由古典概型的概率计算公 式得: 课后思 考: (1)在标准化考试中既有单选题又有多选题,多选题是从 A,B, C,D 四个选项中选出所有正确的答案,同学们可能有一种感觉,如 果不知道正确答案,多选题更难猜对,这是为什么? (2)假设有 20 道单选题,如果有一个考生答对了 17 道题,他是 随机选择的可能性大,还是他掌握了一定知识的可能性大? 学生先思 考再回 答,教师 对学生没 有注意到 的关键点 加以说 明。 让学生明确决 概率的计算问 题的关键是:先 要判断该概率 模型是不是古 典概型,再要找 出随机事件 A 包含的基本事 件的个数和试 验中基本事件 的总数。 巩固学生对已 学知识的掌握。 项 目 内 容 师生活动 理论依据或意 图

例3同时掷两个骰子,计算: (1)一共有多少种不同的结果? (2)其中向上的点数之和是5的结果有多少种? (3)向上的点数之和是5的概是多少 利用列表数开 例 解:(1)拥一个酸子的结果有6种,我们把两个子标上记号1, 结合和分类 以使区分,由于1号骰子的结果都可以与2号股子的任意一个结果 论,既能形象] 配对,我们用一个“有序实数对”来表示组成同时掷两个骰子的 观地列出基本 个结果(如表),其中第一个数表示1号骰子的结果,第二个数表 电件的总数,又 示2号骰子的结果。(可由列表法得到 先给出问 能做到列举的 题,再让 不雨不漏深化 1 3 4 5 6 学生完 成,然后 巩固对古奥概 型及其概率计 过分 6:58 引导学生 算公式的理解 分析问 和用列举法来 题,发现 计一此制 析 事件所含基 事件的个数及 题。 事件发生的框 引导学生 用表安 培养学生运用 列举试路 中的基本 数形结合的思 ,提高发现 事件的总 题、分析问题 数。 解决问膜的能 由表中可知同时辄两个酸子的结果共有6种, 力,增强学生数 (2)在上面的结果中,向上的点数之和为5的结果有4种,分别为 成学习数号 识的积极态度 (1,4),(2,3),(3,2),(4,1D (3)由于所有36种结果是等可能的,其中向上点数之和为5的 果(记为事件A)有4种,因此,由古典概型的概率计算公式可得 灰 KA) =A所包含的基本事件的个数4.1 基本事件的总数 360
教 学 过 程 分 析 四 例 题 分 析 推 广 应 用 例 3 同时掷两个骰子,计算: (1)一共有多少种不同的结果? (2)其中向上的点数之和是 5 的结果有多少种? (3)向上的点数之和是 5 的概率是多少? 解:(1)掷一个骰子的结果有 6 种,我们把两个骰子标上记号 1,2 以便区分,由于 1 号骰子的结果都可以与 2 号骰子的任意一个结果 配对,我们用一个“有序实数对”来表示组成同时掷两个骰子的一 个结果(如表),其中第一个数表示 1 号骰子的结果,第二个数表 示 2 号骰子的结果。(可由列表法得到) 由表中可知同时掷两个骰子的结果共有 36 种。 (2)在上面的结果中,向上的点数之和为 5 的结果有 4 种,分别为: (1,4),(2,3),(3,2),(4,1) (3)由于所有 36 种结果是等可能的,其中向上点数之和为 5 的结 果(记为事件 A)有 4 种,因此,由古典概型的概率计算公式可得 先给出问 题,再让 学生完 成,然后 引导学生 分析问 题,发现 解答中存 在的问 题。 引导学生 用列表来 列举试验 中的基本 事件的总 数。 利用列表数形 结合和分类讨 论,既能形象直 观地列出基本 事件的总数,又 能做到列举的 不重不漏。深化 巩固对古典概 型及其概率计 算公式的理解, 和用列举法来 计算一些随机 事件所含基本 事件的个数及 事件发生的概 率。 培养学生运用 数形结合的思 想,提高发现问 题、分析问题、 解决问题的能 力,增强学生数 学思维情趣,形 成学习数学知 识的积极态度