
33二元一次不等式(组)与平面区域 贵州省习水县第一中学杨登平 知识与技能: 1.理解二元一次不等式表示平面区域: 2,掌握确定二元一次不等式表示的平面区域的方法 3.会画出二元一次不等式(组)表示的平面区域,并掌握步骤 过程与方法:让学生通过实验、观察、作图归纳得出结论,体现了数形结合的思想提 高分析问题、解决问题的能力。 情感态度与价值观:培养学生学习数学的兴趣和“用数学”的意识,激励学生大胆探 索,勇于创新的科学精神。 教学重点:二元一次不等式(组)表示平面区域 教学难点:如何确定不等式4x++C>0(或0)表示4x++C=0的哪一创 区域? 敕学过程: 【创设问题情境】 问题1:在平面直角坐标系中,二元一次方程+一2=0表示什么图形?请学生画出来 问题2:写出以二元一次方程件”2=0的解为坐标的点的集合 (引出点集{(x,功?x+-2=0) 问题3:点集{(x,月?+一20】在平面直角坐标系中表示什么图形? 点集{(x,)?+2>0}与点集{(x,)?+-2>0}又表示什么图形 呢9 【讲授新课】
3.3 二元一次不等式(组)与平面区域 贵州省习水县第一中学 杨登平 知识与技能: 1.理解二元一次不等式表示平面区域; 2.掌握确定二元一次不等式表示的平面区域的方法; 3.会画出二元一次不等式(组)表示的平面区域,并掌握步骤; 过程与方法:让学生通过实验、观察、作图归纳得出结论,体现了数形结合的思想提 高分析问题、解决问题的能力。 情感态度与价值观:培养学生学习数学的兴趣和“用数学”的意识,激励学生大胆探 索,勇于创新的科学精神。 教学重点:二元一次不等式(组)表示平面区域. 教学难点:如何确定不等式 表示 的哪一侧 区域? 教学过程: 【创设问题情境】 问题 1:在平面直角坐标系中,二元一次方程 x+y−2=0 表示什么图形?请学生画出来. 问题 2:写出以二元一次方程 x+y−2=0 的解为坐标的点的集合 (引出点集{(x,y) x+y−2=0 }) 问题 3: 点集{(x,y) x+y−20 }在平面直角坐标系中表示什么图形? 点集{(x,y) x+y−2>0 }与点集{(x,y) x+y−2>0 }又表示什么图形 呢? 【讲授新课】

研究问题:在平面直角坐标系中,以二元一次不等式+一2>0的解为坐标的点的集合 {(x,)?种2>0}是什么图形? 引导提间,+)-20的点在哪里?生:直线广上20外 提间:+y-2≠0有哪些情况?生:-20或20 :xy-2=0 师:在平面直角坐标系中,所有的点被直线种上2=0分成三类:即在直线+乒2=0上: 在直线+上2=0的左下方的平面区域内: 在直线+2=0的右上方的平面区域内 师:+-2>0或+2<0他们究竟在分别在哪侧呢? 一、学生实验: 师:1、2两组学生合为A组。3、4两组学生合为B组, A组学生:取右上方的点计算x+y-2的值并判断满足哪个关系 B组学生:取左下方的点计算x+y一2的值并判断满足哪个关系 二、学生清想
研究问题:在平面直角坐标系中,以二元一次不等式 x+y−2>0 的解为坐标的点的集合 {(x,y) x+y−2>0 }是什么图形? 引导提问: 的点在哪里?生:直线 x+y−2=0 外 提问: 有哪些情况?生:x+y−2>0 或 x+y−20 或 x+y−2<0 他们究竟在分别在哪侧呢? 一、学生实验: 师:1、2 两组学生合为 A 组。3、4 两组学生合为 B 组, A 组学生:取右上方的点计算 x+y-2 的值并判断满足哪个关系? B 组学生:取左下方的点计算 x+y-2 的值并判断满足哪个关系? 二、学生猜想

A组:直线+L2=0右上方的任意点(K,月,x+乒2>0都成立 x+y-2-0 B组:直线1:x+-2=0左下方的任意点(x,),x+-20, 因为点P(,)是直线+上2=0上的任意点 所以,对于直线+八2=0右上方的任意点(x,,+2>0都成立 同理,对直线上:+上2=0左下方的任意点(x,,一20的解为坐标的点的集合{(x, )?种2>0}是在直线+一2=0右上方的平面区域
A 组:直线 x+y−2=0 右上方的任意点(x,y), x+y−2>0 都成立. B 组:直线 l: x+y−2=0 左下方的任意点(x,y), x+y−2 y0, 所以, x+y> x0+ y0=0, 所以, x+y−2> x0+ y0 −2=0, 即 x+y−2>0, 因为点 P(x0,y0)是直线 x+y−2=0 上的任意点, 所以,对于直线 x+y−2=0 右上方的任意点(x,y), x+y−2>0 都成立. 同理, 对直线 l: x+y−2=0 左下方的任意点(x,y), x+y−20 的解为坐标的点的集合{(x, y) x+y−2>0 }是在直线 x+y−2=0 右上方的平面区域

类似地,在平面直角坐标系中,以二元一次不等式+上2<0的解为坐标的点的集合 (x,)?+一2<0)是在直线种上2=0左下方的平面区域. 提出:直线x+一2=0的两侧的点的坐标代入*一2中,得到的数值的符号,仍然会 “同侧同号,异侧异号”吗? 通过分析引导学生得出一般二元一次不等式表示平面区域的有关结论。 四、一般二元一次不等式表示平面区域 结论:在平面直角坐标系中, (1)二元一次不等式A++O0表示直线A++C0某一侧所有点组成的平面区域, A++C0则表示直线另一侧所有点组成的平面区域:(同侧同号,异侧异号) (2)有等则实,无等则虚: (3)取点定域,原点优先 -五.应用举例 例1画出不等式2x+y-6<0表示的平面区域。 解:先画直线2不+6=0(画成虚线) 取原点(0,0),代入2不+6,2×0+0-6=-6<0 “原点在2x+6<0表示的平面区域内,不等式2x+6<0表示的区域如图 反思归纳: 画二元一次不等式表示的平面区域的方法和步骤 (1)画线定界(意实、虚线) (2)取点定域原点优先
类似地, 在平面直角坐标系中, 以二元一次不等式 x+y−20 表示直线 Ax+By+C=0 某一侧所有点组成的平面区域, Ax+By+C<0 则表示直线另一侧所有点组成的平面区域; (同侧同号,异侧异号) (2)有等则实,无等则虚; (3)取点定域,原点优先. 五.应用举例 例 1 画出不等式 2x+y-6<0 表示的平面区域。 解:先画直线 2 +y-6=0(画成虚线). 取原点(0,0),代入 2 +y-6,∵2×0+0-6=-6<0, ∴原点在 2 +y-6<0 表示的平面区域内,不等式 2 +y-6<0 表示的区域如图: 反思归纳: 画二元一次不等式表示的平面区域的方法和步骤: (1)画线定界(注意实、虚线); (2)取点定域.原点优先
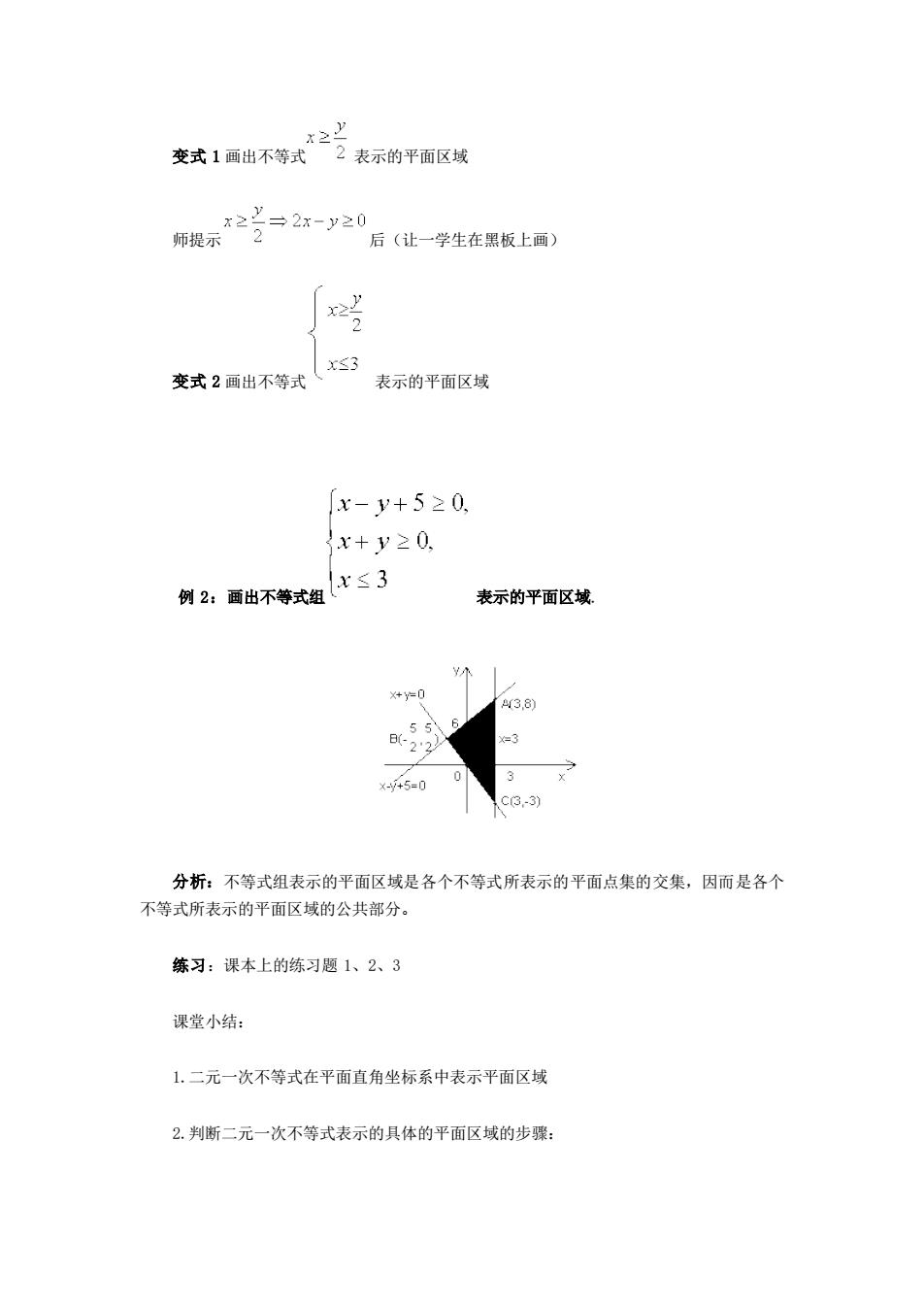
安式1酒出不特式之号我标粉面区线 师示*2-20 (让一学生在黑板上画 变式2画出不等式x3 表示的平面区域 x-y+5≥0 x+y≥0. 例2,面出不等式组x3 表示的平面区域。 40 -y45=0 3.3) 分析:不等式组表示的平面区域是各个不等式所表示的平面点集的交集,因而是各个 不等式所表示的平面区域的公共部分。 练习:课本上的练习题1、2、3 课堂小结: 1,二元一次不等式在平面直角坐标系中表示平面区域 2.判断二元一次不等式表示的具体的平面区域的步骤:
变式 1 画出不等式 表示的平面区域 师提示 后(让一学生在黑板上画) 变式 2 画出不等式 表示的平面区域 例 2:画出不等式组 表示的平面区域. 分析:不等式组表示的平面区域是各个不等式所表示的平面点集的交集,因而是各个 不等式所表示的平面区域的公共部分。 练习:课本上的练习题 1、2、3 课堂小结: 1.二元一次不等式在平面直角坐标系中表示平面区域 2.判断二元一次不等式表示的具体的平面区域的步骤:

(1)画直线定界(要注意实、虚线),简称:定界: (2)用特殊点定区域: 3.作二元一次不等式组表示的平面区域的方法: (1作直线(注意虚实)(2取点定域.原点优先(③)作出公共区域 布置作业:习题3.3A组 第1题.第2题
(1)画直线定界(要注意实、虚线),简称:定界; (2)用特殊点定区域; 3.作二元一次不等式组表示的平面区域的方法: ⑴作直线(注意虚实) ⑵取点定域.原点优先 ⑶作出公共区域 布置作业:习题 3.3 A 组 第 1 题. 第 2 题