
试卷代号:2588 座位■■ 国家开放大学(中央广播电视大学)2014年春季学期“开放专科”期末考试 管理线性规划入门 试题 2014年7月 题 号 三 总 分 分 数 得分 评卷人 一、单项选择题(每小题4分,共20分) 1.下列( )为3阶单位矩阵。 17 100 11 1 C.01 0 D.11 00 1 11 1 2.线性规划模型的标准形式要求目标函数( ). A.求最大值 B.不求最优值 C.没有限制 D.求最小值 3.在MATLAB软件中,矩阵转置运算的运算符是(). A.’ B.T C.并 D.A 4.在MATLAB软件的命令窗口(command window)中输入矩阵运算的命令语句为: >>2*B'¥A,则进行的矩阵运算为()。 A.2BA B.2BTA C.2ABT D.2ATB 5.在MATLAB软件的命令窗口(command window)中输人的命令语句为:>>A3,则 进行的运算为()。 A.求矩阵A的逆 B.求矩阵A的3次方 C.求矩阵A的转置 D.将矩阵A化为行简化阶梯型矩阵 2009
试卷代号 座位号仁口 国家开放大学(中央广播电视大学 4年春季学期"开放专科"期末考试 管理线性规划入门试题 2014 年7 |题号|一|二|三|总分| |分数 I I I I |得分|评卷人| I I I 一、单项选择题{每小题 4分,共 0分} 1.下列( )为 3阶单位矩阵. Ci :1 Diiil 2. 性规 准形 要求 ) • A. 值B.不求最 C. 有 限制D. 3. 在MATLAB 运算 算符是 〈λ A. ' B. T C. 铸D.II 4. 在MATLAB 口(command window) 入 短 »2 势B' 传A ). ~2M &2WA C. 2ABT D. 2ATB 5. 在MATLAB软件 口(command window) 输入 令语 进行的运算为 A. 阵A 逆B.求矩阵A 的3 C. 求矩阵A 置D. 阵A 阶梯 2009

得分 评卷人 二、计算题(每小题10分,共30分) 311] 117 6.设A= 212,B=2-10,计算:BA. 1 23 7,将下列线性规划模型的标准形式表示成矩阵形式: min S=6x1+5xz -3x1-x2≤-10 -4x1-8x2≤-34 4x1+3x2=21 x1≥0,x2≥0 8.某线性方程组的增广矩阵D对应的行简化阶梯形矩阵为 1000 21 0100-1 D= 00101 0001-3 判断该线性方程组解的情况,若有解,写出该方程组的解。 得 分 评卷人 三、应用题(第9题20分,第10,11题各15分,共50分)】 9.某涂料厂生产甲、乙两种涂料,由A,B,C三种原料混合制成。生产一桶甲涂料需要A 原料30公斤,B原料10公斤,C原料10公斤;生产一桶乙涂料需要A原料32公斤,B原料11 公斤,C原料7公斤。该厂每月供应A原料5000公斤,B原料2500公斤,C原料1500公斤. 每桶甲涂料可获利10元,每桶乙涂料可获利9元。 (1)试写出使该厂获得利润最大的线性规划模型; (2)将该线性规划模型化为标准形式,并写出用MATLAB软件计算该线性规划问题的命 令语句。 2010
|得分|评卷人|- .!.L.... 算题每小题 0分,共 0分} I I 一 ' 叫:;|B=i:1j 7. 下列 标准 式表 成矩 min S=6xj +5xz -4Xj- xzζ-34 4Xj +3xz=21 Xj ,Xz 注0 8. 性方程 阵D 对应 阵为 10002 o 100 一1 D= 00101 o 0 0 1 -3 判断该线性方程组解的情况,若有解,写出该方程组的解. |得分|评卷入| I I I 三、应用题{第 9题 0分,第 0, 11题备 5分,共 0分} 9. 厂生 两种涂 三种原料混 产一 要A 原料 0公斤 B原料 0公斤, C原料 0公斤 z生产一桶乙涂料需要 A原料 2公斤 B原料 11 公斤, C原料 7公斤.该厂每月供应 A原料 0公斤 B原料 2 5 0公斤, C原料 0公斤. 每桶甲涂料可获利 0元,每桶乙涂料可获利 9元. (1)试写出使该厂获得利润最大的线性规划模型 (2) AT 该线性 的命 令语句. 2010
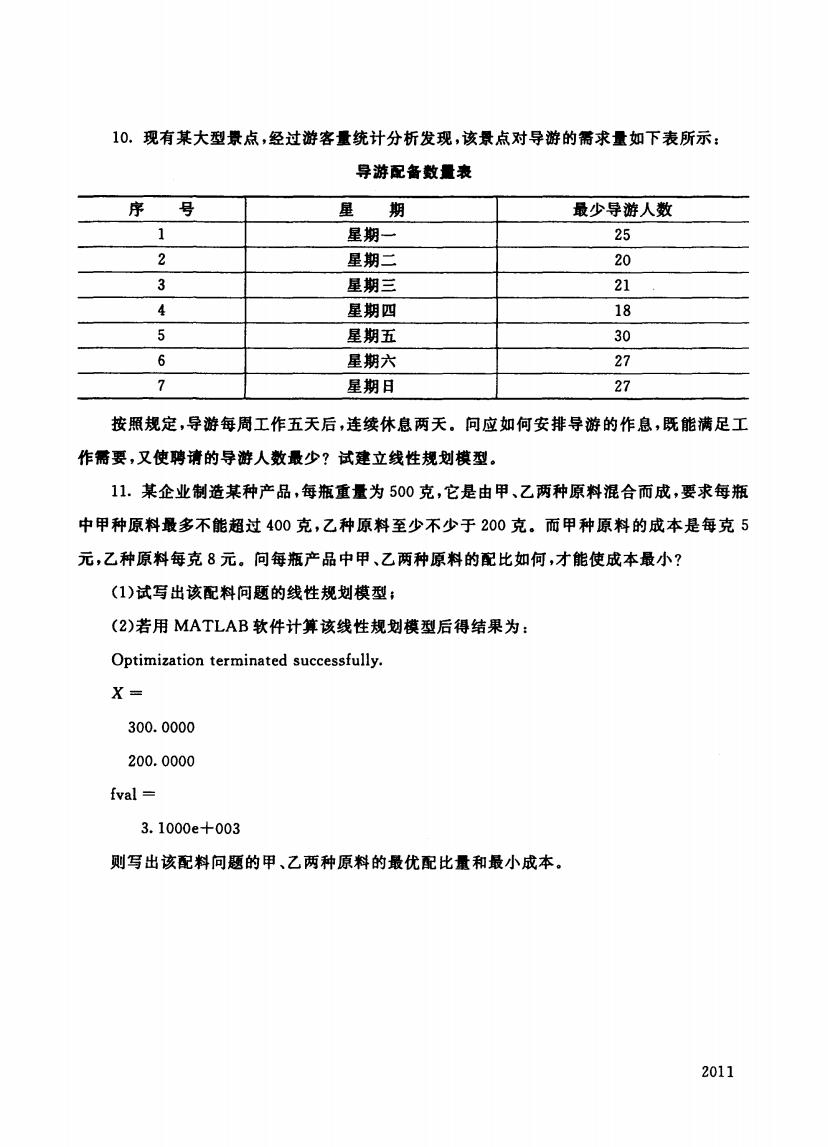
10.现有某大型景点,经过游客量统计分析发现,该景点对导游的需求量如下表所示: 导游配备数量表 序 号 星期 最少导游人数 1 星期一 25 2 星期二 20 3 星期三 21 4 星期四 18 5 星期五 30 6 星期六 27 7 星期日 27 按照规定,导游每周工作五天后,连续休息两天。问应如何安排导游的作息,既能满足工 作需要,又使聘请的导游人数最少?试建立线性规划模型。 11.某企业制造某种产品,每瓶重量为500克,它是由甲、乙两种原料混合而成,要求每瓶 中甲种原料最多不能超过400克,乙种原料至少不少于200克。而甲种原料的成本是每克5 元,乙种原料每克8元。问每瓶产品中甲、乙两种原料的配比如何,才能使成本最小? (1)试写出该配料问题的线性规划模型; (2)若用MATLAB软件计算该线性规划模型后得结果为: Optimization terminated successfully X= 300.0000 200.0000 fval 3.1000e+003 则写出该配料问题的甲、乙两种原料的最优配比量和最小成本。 2011
10. 某大 析发 景点 导游 表所示z 导游配备鼓量襄 最少导游人数 1 星期一 25 2 星期二 20 3 星期三 21 4 星期四 18 5 星期五 30 6 星期六 27 7 星期日 27 按照规定,导游每周工作五天后,连续休息两天.问应如何安排导游的作息,既能满足工 作需要,又使聘请的导部人数最少?试建立线性规划模型. 1. 企业 种产 为500 原料混合 中甲种原料最多不能超过 0克,乙种原料至少不少于 0克.而甲种原料的成本是每克 元,乙种原料每克 8元.问每瓶产品中甲、乙两种原料的配比如何,才能使成本最小? (1)试写出该配料问题的线性规划模型 (2) 用MATLAB 性规 后得结 Optimization terminated successfully. X= 300.0000 200.0000 fval = 3.1000e+003 则写出该配料问题的甲、乙两种原料的最优配比量和最小成本. 2011

试卷代号:2588 国家开放大学(中央广播电视大学)2014年春季学期“开放专科”期末考试 管理线性规划入门试题答案及评分标准 (供参考) 2014年7月 一、单项选择题(每小题4分,共20分) 1.C 2.D 3.A 4.B 5.B 二、计算题(每小题10分,共30分)】 111]3117 646 6.BA=2 -10212=410 10分 0123434 7,该线性规划问题的矩阵形式为: min S=CX GX≤H AX=B X>LB 其中c=61c-[-],H=[9]A=,B=2]-X=[],B= 10分 8。行简化阶梯形矩阵对应的线性方程组为 =2 =-1 =1 x4=-3 因为没有出现方程0=(≠0),所以该方程组有解,且线性方程的个数为4,等于变量的个 数4,所以该线性方程组有惟一解。 该线性方程组的解为 x1=2,x2=-1,x3=1,x4=-3 10分 三、应用题(第9题20分,第10,11题各.15分,共50分) 9.(1)设该厂每月生产甲、乙两种涂料分别为x1,x2(桶),则线性规划模型为: max S=10x1+9z2 [30x1+32x2≤5000 10x1+11x2≤2500 10分 10x+7x2≤1500 x1xz≥0 2012
试卷代号 2 5 国家开放大学{中央广播电视大学 4年春季学期"开放专科"期末考试 管理线性规划入门试题答案及评分标准 (供参考〉 2014 年7 -、单项选择题{每小题 4分.共 0分} 1.C 2. 0 3. A 4. B 二、计算题{每小噩 0分,共 0分} 6. BA= 12 -1 0 I 12 1 2 I = 14 1 0叶 1111 2 31 14 3 41 7. 线性 形式 5.B 10 min S=CX rGXζH ~AX=B lX LB C po G -- H -- A -- B nL'i X LB 8. 梯形矩 性方程 rXI = 2 I Xz =-1 I X3 = 1 l X. =-3 因为没有出现方程 .所以该方程组有解,且线性方程的个数为.等于变量的个 .所以该线性方程组有惟一解. 该线性方程组的解为 Xl =2.xz = -1 ,x 3 =1. 10 三、应用题{第 9题 0分,第 0, 11题备 5分,共 0分} 9. (1)设该厂每月生产甲、乙两种涂料分别为 .则线性规划模型为 max S=10xI +9xz ''lll-dEl--IK qdTAIAZ oooi zzztF311'nunu nunu 10 2012

(2)令S=S,此线性规划模型的标准形式为: min S'=-10x1-9x2 [30x1十32x2≤5000 10x1+11,x2≤2500 15分 10x+7x2≤1500 x1,x2≥0 计算该线性规划问题的MATLAB语句为: >>clear; >>C=[-10-9]; >>G=[3032;1011;107]: >>H=[500025001500]'; >>LB=[00]': >>[X,fual]=linprog(C,G,H,[],[],LB) 20分 10.设x,为序号为j的星期j开始上班的人数,则x,≥0(j=1,2,…,7),又设一周上班的 导游人数总和为S,则所求线性规划模型为: minS=x1十x2十x3十x,十x5十x6十x x1十x4+xs十x6+x1≥25 x1十x2十x5十x6十x1≥20 x1十x2十x3十x6+x1≥21 x1十x2十x3十x4十x7≥18 15分 x1十x2十x3十x4十x5≥30 x2十x3十x4十x5十x6≥27 xg十x4十x5十x6十x,≥27 xj≥0(j=1,2,…,7) 11.(1)设每瓶产品中甲、乙两种原料的含量分别为x1,x2(克),则线性规划模型为: min S=5x1+8x2 [x1≤400 x2≥200 10分 x1十x2=500 x1≥0,x2≥0 (2)根据计算结果得:甲原料300克、乙原料200克为最小成本的配比量,最小成本为 3100元. 15分 2013
(2) 线性 标准形式 min S'= 一10xl- xz (30Xl +32xz~ 110xl +l1 2 5 110x+ 7xz~ 15 15 计算该线性规划问题的 B语句为 »clear; »C=[-10 -9J; »G=[30 32; 10 11; 10 7J; »H=[5000 2500 1500J »LB=[O »[X. !alJ = linprog{C.G. H. 20 10. 序号 星期 始上 (j=1 •2 •••••7) .又设一周上班的 导游人数总和为 .则所求线性规划模型为 min S=Xl 十XZ+X3+岛+XS+X6+X7 XI+X. +Xs+X6 +X7 Xl +xz+xs +X6+X7 Xl +XZ +X3 +X6 +X7 Xl +XZ+X3 十X.+X1; Xl +Xz+X3+X. +Xs XZ+X3+X. +XS +X6 X3+X. +XS 十X6+X7~27 Xj 1, 11. (1)设每瓶产品中甲、乙两种原料的含量分别为 l ' {克) .则线性规划模型为: min S=5Xl +8xz idoo Xz 注200 10 Xl +XZ =500 Xl 注O.XZ (2) 得z 料300 料200 成 本 小 成 3100 15 2013