
试卷代号:1009 座位号■■ 中央广播电视大学2010-2011学年度第-学期“开放本科”期末考试(半开卷) 离散数学(本)试题 2011年1月 题 号 二 三 四 五 六 总 分 分 数 得分 评卷人 一、单项选择题(每小题3分,本题共15分) 1.若集合A={a,{1}},则下列表述正确的是(). A.{1}∈A B.(1)CA C.{a}∈A D.O∈A 2.设图G=,∈V,则下列结论成立的是(). A.deg(v)=2E] B.deg(v)=E C.deg() D.∑deg()=21El 3.如图一所示,以下说法正确的是( A.(e,c)是割边 B.(d,e)是割边 C.(b,a)是割边 D.(b,c)是割边 4.命题公式(PVQ)的合取范式是( ). 图 A.P B.(PAQ) C.(PVP) D.(PVQ) 5.下列等价公式成立的为(). A.P∧Q台PVQ B.Q-→P台P→Q C.P∧P台Q∧Q D.-PVPeQ 69
试卷代号: 1009 座位号 中央广播电视大学 2011 度第 放本 末考 离散数学(本)试题 2011 年1 题号 /-2 总分 分数 得分|评卷人 一、单项选择题(每小题3分,本题共 5分) 1.若集合 α, },则下列表述正确的是( ). A. {I} B. {l} c A C. {α} EA D.0εA 2. 则下列 论成 ). A. deg(v)=2IE! C. ~deg(v) =1 E I 3. 正确 A. (e , c) B. C. (b D. (b 是割 4. 命题公式 式是 B. deg(v)= lEI D. ~deg(v) =2 I E I vEV G .0 O 图一 且) ι· '0 d A.P B.(P c. (P VP) D. (P VQ) 5. 等价公式 ). A.P ∞PVQ B. -'Q →Q c. -, -, D.-, 69

得分 评卷人 二、填空题(每小题3分,本题共15分)】 6.设集合A={0,1,2},B={1,2,3,4},R是A到B的二元关系, R={|x∈A且y∈B且x,y∈A∩B} 则R的有序对集合为 7.设G是连通平面图,v,e,r分别表示G的结点数,边数和面数,则v,e和r满足的关系 式 8.设G=是有20个结点,25条边的连通图,则从G中删去 条边,可以 确定图G的一棵生成树. 9.无向图G存在欧拉回路,当且仅当G所有结点的度数全为偶数且 10.设个体域D={1,2},则谓词公式HxA(x)消去量词后的等值式为 得分 评卷人 三、逻辑公式翻译(每小题6分,本题共12分) 11.将语句“如果小李学习努力,那么他就会取得好成绩.”翻译成命题公式, 12.将语句“小张学习努力,小王取得好成绩.”翻译成命题公式. 得 分 评卷人 四、判断说明题(每小题7分,本题共14分) 判断下列各题正误,并说明理由. 13.如果R1和R2是A上的自反关系,则R1∩R2是自反的. 14.如图二所示的图中存在一条欧拉回路· 图二 70
得分|评卷人 二、填空题{每小题 3分,本题共 5分) 6. 合A={0 ,1 ,2} ,B= {l ,2 ,3 ,R 是A 到B 二元 R= { Ix εB 门B} R的有序对集合为 7. 设G 是连通平 示G 边数 • 8. 有20 ,25 条边 连通 从G 确定图 G的一棵生成树. 9. 图G 当G 数全 10. 设个体域 1, xA(x) 得分|评卷人 三、逻辑公式翻译{每小题 6分,本题共 2分) 1. 将语 他就会取 好成 题公式 12. 语句 题公 得分|评卷人 四、判断说明题(每小题 7分,本题共 4分) 判断下列各题正误,并说明理由. 13. 果R 则R 14. 二所 在一 图二 70 条边,可以 • •

得分 评卷人 五、计算题(每小题12分,本题共36分) 15.设A={{2},1,2},B={1,{1,2},试计算 (1)(A-B); (2)(A∩B); (3)AX B. 16.设G=,V={1,2,,u4,s},E={(U1,3),(v2,3),(2,u4),(3,u4), (w3,)},试 (1)给出G的图形表示; (2)写出其邻接矩阵; (3)求出每个结点的度数; (4)画出其补图的图形. 17.设谓词公式3x(A(x,y)∧HB(x,y,))∧HyC(y,z),试 (1)写出量词的辖域; (2)指出该公式的自由变元和约束变元· 得 分 评卷人 六、证明题(本题共8分) 18.试证明集合等式AU(B∩C)=(AUB)∩(AUC). 71
得分|评卷人 五、计算题{每小题 2分,本题共 6分) 15. } , {l {l } , (1) (A- B); (2)(An B) ; (3)AX B. 16. V= {VI' E = { ( VI • V3 ) • (吨 V3 ) • (吨 V4 ) • ( V3 • V4 ) , (叫,阿) } .试 (1)给出 G的图形表示; (2) 邻接 (3) (4) 其补 17. 公式 x(A(x.y) 'v zB(x 川z» 'v yC(y (1)写出量词的辖域; (2) 该公式 得分!评卷人 六、证明题(本题共 8分) 18. 集合 C)=(AU B) n(AUC). 71

试卷代号:1009 中央广播电视大学2010一2011学年度第一学期“开放本科”期未考试(半开卷) 离散数学(本) 试题答案及评分标准 (供参考) 2011年1月 一、单项选择题(每小题3分,本题共15分) 1.A 2.D 3.B 4.D 5.C 二、填空题(每小题3分,本题共15分)】 6.{,,,} 7.v-e十r=2 8.6 9.连通 10.A(1)ΛA(2) 三、逻辑公式翻译(每小题6分,本题共12分) 11.设P:小李学习努力,Q:小李会取得好成绩, (2分) P→Q (6分) 12.设P:小张学习努力,Q:小王取得好成绩, (2分) P∧Q. (6分) 四、判断说明题(每小题7分,本题共14分) 13.正确· (3分) R和R2,是自反的,Hx∈A,∈R1,∈R2, 则∈R1∩R2, 所以R1∩R2是自反的. (7分) 14.正确, (3分) 因为图G为连通的,且其中每个顶点的度数为偶数, (7分) 五、计算题(每小题12分,本题共36分) 15.(1)A-B={2,{2}} (4分) (2)A∩B={1} (8分) (3)A×B={,,,,,} (12分) 72
试卷代号 0 0 中央广播电视大学 2011 年 度 第 一 学 末考 离散数学(本)试题答案及评分标准 (供参考) 2011 年1 一、单项选择题(每小题 3分,本题共 5分) 1. A 2. D 3. B 二、填空题(每小题 3分,本题共 5分} 6. { . . . } 7. 十r=2 4. D 5. C 8. 6 9. 10. (l 八A(2) 三、逻辑公式翻译(每小题 6分,本题共 2分) 1. 设P: 李学 取得 成绩 P• Q. 12. 四、判断说明题(每小题 7分,本题共 4分) 13. 乱和凡,是自反的 V x ε凡 >仨凡, nR2 • (2 (6 (2 (6 c3分) (7 c3分) (7 所以 凡是自反的. 14. 正确 因为图 G为连通的,且其中每个顶点的度数为偶数. 五、计算题(每小题 2分,本题共 6分) 15. (l)A - B = {2 . {2 } } (4 (2)A 门B= {l (8 (3)A X B= {. •. . . } (1 72
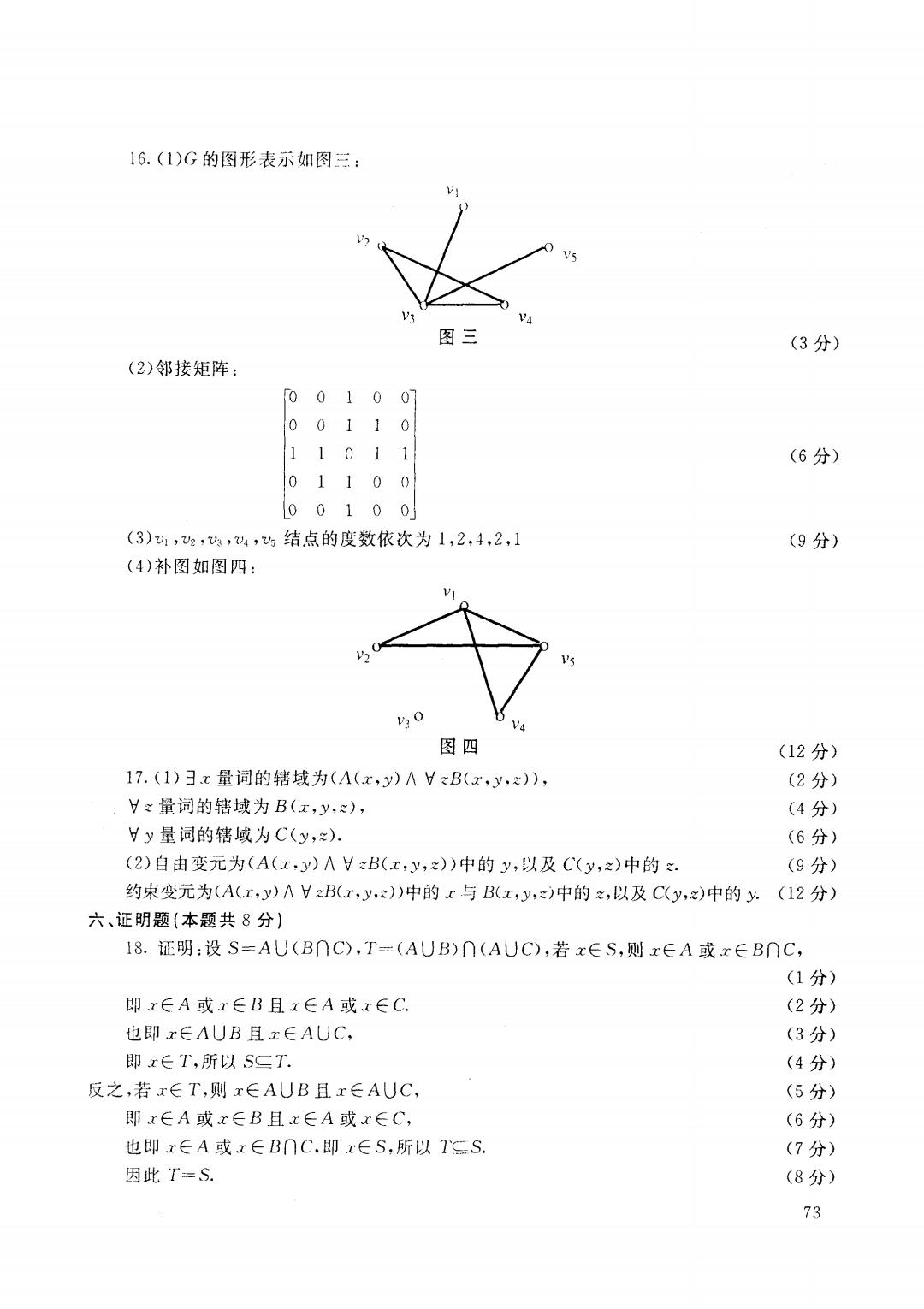
16.(1)G的图形表示如图三: 图三 (3分) (2)邻接矩阵: 0010 07 00110 11011 (6分) 01100 L00100 (3)1,2,,4,5结点的度数依次为1,2,4,2,1 (9分) (4)补图如图四: 图四 (12分) 17.(1)3x量词的辖域为(A(x,y)∧HxB(x,y,之), (2分) Vx量词的辖域为B(x,y,), (4分) Hy量词的辖域为C(y,~). (6分) (2)自由变元为(A(x,y)AHB(x,y,)中的y,以及C(y,之)中的. (9分) 约束变元为(A(x,y)∧HB(x,y,)中的x与B(x,y,)中的,以及C(y,)中的y.(12分) 六、证明题(本题共8分) 18.证明:设S=AU(B∩C),T=(AUB)∩(AUC),若x∈S,则x∈A或x∈B∩C, (1分) 即x∈A或x∈B且x∈A或x∈C. (2分) 也即x∈AUB且x∈AUC, (3分) 即x∈T,所以S二T. (4分) 反之,若x∈T,则x∈AUB且x∈AUC, (5分) 即x∈A或x∈B且x∈A或x∈C, (6分) 也即x∈A或x∈B∩C,即x∈S,所以ICS. (7分) 因此T=S. (8分) 73
16. (1)G 的 图 VI Vs ) V1 V4 图一一一 (3 (2) m O O 。「 O 1 I (6 1 O (3)叭,屿, ,叫, 结点 1, 2, 4, 2, (9 (4) VI V2 Vs V,O V4 (1 (2 (4 (6 (9 (1 2 图四 17. (1 辖域 C: 'if zB(:l' ,y.z» , 'if 辖域 (x , y ,z) , 'if (2) 'if zB(x ,z» 的y ,z) 约束变元为 'if zB(x ,y ,z» .1: 与B(x ,y ,z) 的z ,z) 的y. 六、证明题{本题共 18. A U B> U C) (1分) (2 (3 (4 (5 (6 (7 (8 c. 也即 U B U C 毛丁,所以 I' 反之,若 正AUB ε A Nil ε B ε( 也即 C,即 S,所以 因J1t T=S. 73