
全程设计 第十一章立体几何初步 习题课一一空间几何体
第十一章立体几何初步 习题课——空间几何体
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导知 课标定位素养阐释 1认识柱体、锥体、台体、球及简单组合体的结构特征,并能 运用这些特征描述现实生活中简单物体的结构: 2.会用斜二测画法作出平面图形和简单空间图形(棱柱、棱 锥、棱台等)的直观图. 3.会求柱体、锥体、台体、球的表面积和体积 4.加强直观想象、逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.认识柱体、锥体、台体、球及简单组合体的结构特征,并能 运用这些特征描述现实生活中简单物体的结构. 2.会用斜二测画法作出平面图形和简单空间图形(棱柱、棱 锥、棱台等)的直观图. 3.会求柱体、锥体、台体、球的表面积和体积. 4.加强直观想象、逻辑推理和数学运算能力的培养

导航 课前·基础认知 一、空间几何体的结构特征 L填空: (1)多面体的结构特征 多面体 结构特征 有两个面① ,且该多面体的顶点都在这两个面上, 棱柱 其余各面都是平行四边形 一个多面体有一个面是多边形,且其余各面都是有一个 棱锥 ② 的三角形 用③ 棱锥底面的平面去截棱锥,所得截面与底面间的 棱台 多面体
导航 一、空间几何体的结构特征 1.填空: (1)多面体的结构特征 多面体 结构特征 棱柱 有两个面①互相平行,且该多面体的顶点都在这两个面上, 其余各面都是平行四边形 棱锥 一个多面体有一个面是多边形,且其余各面都是有一个 ②公共顶点的三角形 棱台 用③平行于棱锥底面的平面去截棱锥,所得截面与底面间的 多面体 课前·基础认知
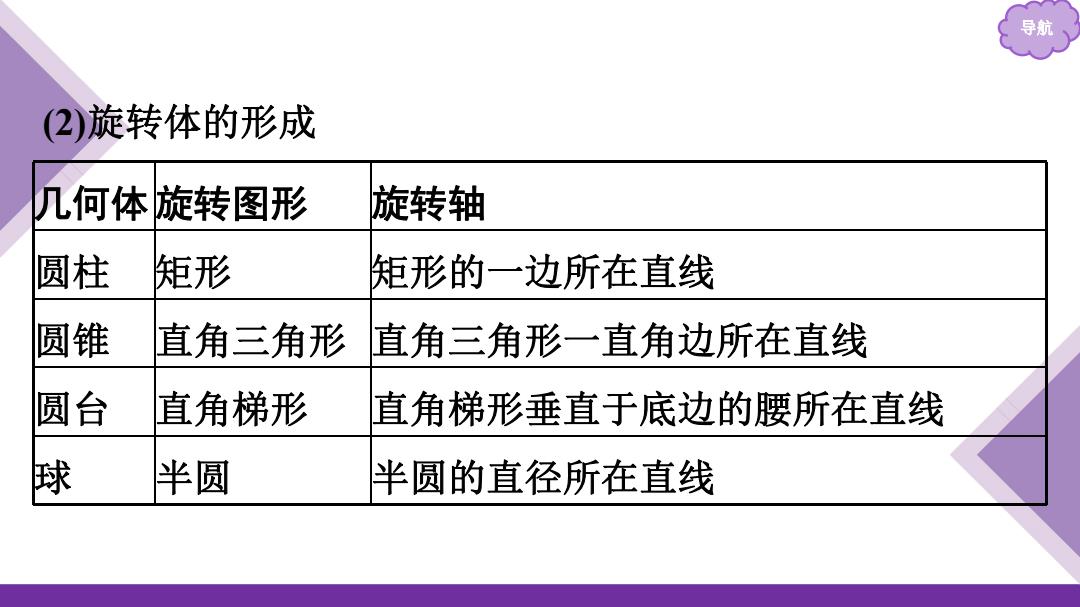
导航 (2)旋转体的形成 几何体旋转图形 旋转轴 圆柱 矩形 矩形的一边所在直线 圆锥 直角三角形 直角三角形一直角边所在直线 圆台 直角梯形 直角梯形垂直于底边的腰所在直线 球 半圆 半圆的直径所在直线
导航 (2)旋转体的形成 几何体 旋转图形 旋转轴 圆柱 矩形 矩形的一边所在直线 圆锥 直角三角形 直角三角形一直角边所在直线 圆台 直角梯形 直角梯形垂直于底边的腰所在直线 球 半圆 半圆的直径所在直线
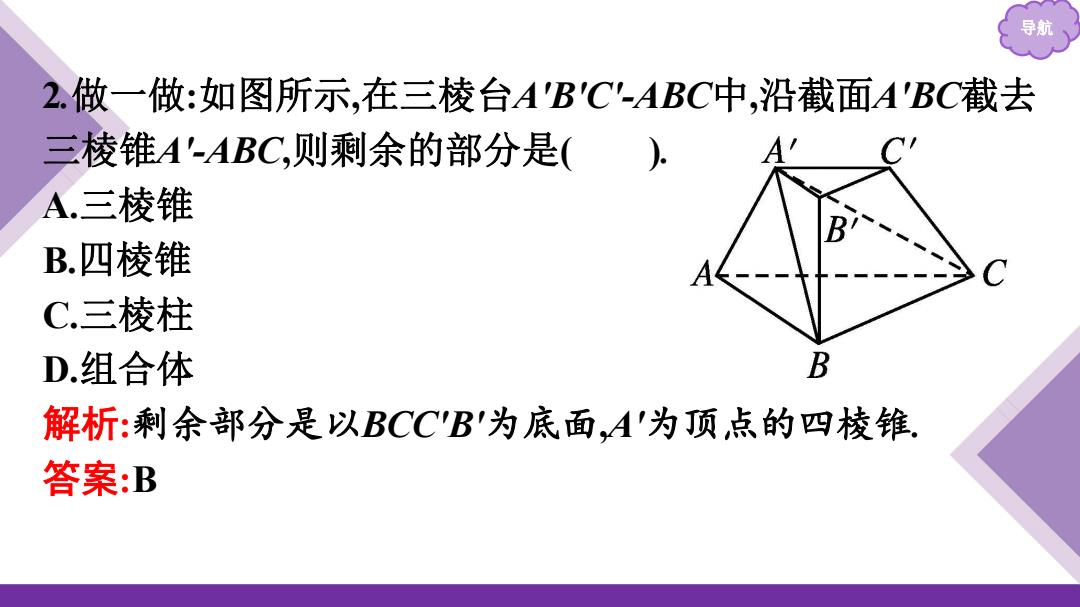
2.做一做:如图所示,在三棱台A'B'C-ABC中,沿截面A'BC截去 三棱锥A'-ABC,则剩余的部分是( A三棱锥 B.四棱锥 C.三棱柱 D组合体 B 解析:剩余部分是以BCCB为底面,A'为顶点的四棱锥, 答案:B
导航 2.做一做:如图所示,在三棱台A'B'C'-ABC中,沿截面A'BC截去 三棱锥A'-ABC,则剩余的部分是( ). A.三棱锥 B.四棱锥 C.三棱柱 D.组合体 解析:剩余部分是以BCC'B'为底面,A'为顶点的四棱锥. 答案:B

二、直观图 1填空 ()画法:斜二测画法 (2)规则:a.原图形中x轴、y轴、z轴两两垂直,直观图中,x'轴和y轴 正方向的夹角为① ,过x轴与y轴的交点作z轴对应 的z轴,且z轴垂直于x轴 b.原图形中与x轴平行(或重合)的线段画成与x轴平行(或重合)的 线段,且长度不变;原图形中与y轴平行(或重合)的线段画成与y轴 平行(或重合)的线段,且长度为② ;原图形中与轴 平行(或重合)的线段画成与z'轴平行(或重合)的线段,且长度不变
导航 二、直观图 1.填空: (1)画法:斜二测画法. (2)规则:a.原图形中x轴、y轴、z轴两两垂直,直观图中,x'轴和y'轴 正方向的夹角为① 45°或135° ,过x'轴与y'轴的交点作z轴对应 的z'轴,且z'轴垂直于x'轴. b.原图形中与x轴平行(或重合)的线段画成与x'轴平行(或重合)的 线段,且长度不变;原图形中与y轴平行(或重合)的线段画成与y'轴 平行(或重合)的线段,且长度为②原来长度的一半;原图形中与z轴 平行(或重合)的线段画成与z'轴平行(或重合)的线段,且长度不变

导期 2.做一做:在平行四边形ABCD中,∠BAD=30°,AB=4,AD=2, 则它的直观图的面积为 解析:平行四边形ABCD的面积S=2×2×AB×ADXsin30°=4,则 直观图的面积S4保× =V2. 答案:v2
导航 2.做一做:在平行四边形ABCD中,∠BAD=30° ,AB=4,AD=2, 则它的直观图的面积为
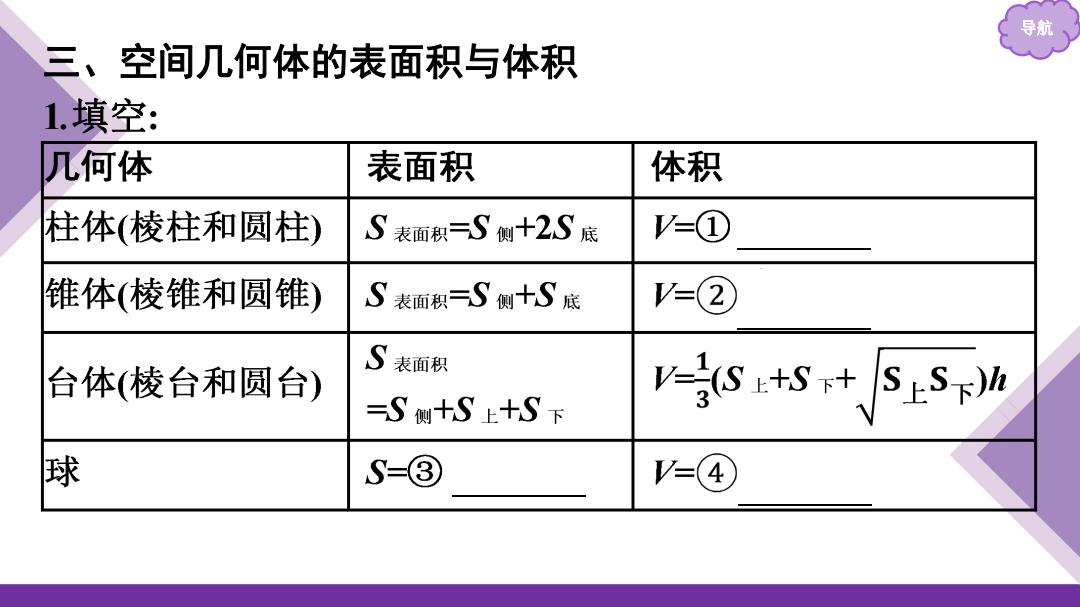
导航 三、空间几何体的表面积与体积 1填空: 几何体 表面积 体积 柱体(棱柱和圆柱) S表面积=S侧十2S底 V=① 锥体(棱锥和圆锥) S表面积=S侧十S底 V=② S 表面积 台体(棱台和圆台) =S侧+S上+S下 V-H(S+S++SLS)h 7 球 S=③ V=(4
导航 三、空间几何体的表面积与体积 1.填空:
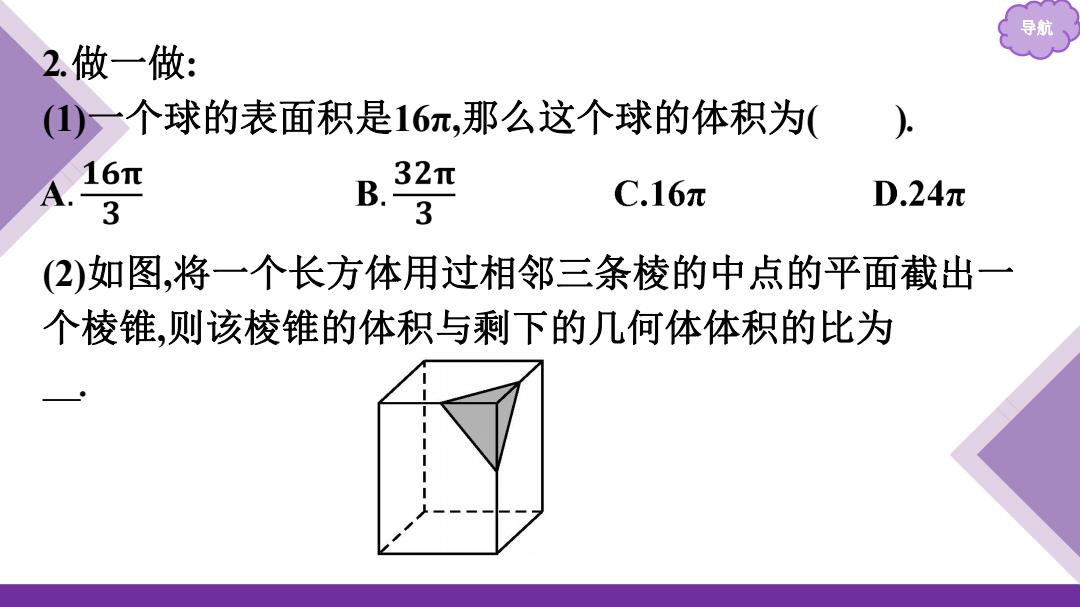
导航 2.做一做: (一个球的表面积是16元,那么这个球的体积为( ) 16π 32π A. C.16元 3 D.24元 (2)如图,将一个长方体用过相邻三条棱的中点的平面截出 个棱锥,则该棱锥的体积与剩下的几何体体积的比为
导航 2.做一做: (1)一个球的表面积是16π,那么这个球的体积为( ). (2)如图,将一个长方体用过相邻三条棱的中点的平面截出一 个棱锥,则该棱锥的体积与剩下的几何体体积的比为