复习课 1.空间向量与立体几何 基础巩固 L.在空间四边形ABCD中,连接AC,BD,若△BCD是正三角形,且E为其中心,则AE+BC- -而的化简结果为( A.AB B.2BD C.0 D.2DE 解析:如图,设BC的中点为F,E是DF的三等分点, D呢=F ∴B武=F,A正+BC-D正-AD=AE+BF-DF-AD=AF+D-AD=AD- AD=0. 答案:C 2.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,),若a,b,c三向量共面,则实数1等于() A号 B C.4 D号 析:若a,b,c三向量共面,则存在xy使c=xa+b, (7=2x-y, 即5=-x+4y,解得1-钙故选D, (a=3x-2y, 答案D 3.己知平面a的一个法向量为n=(2,-2,4),AB=(-3,1,2),点A不在a内,则直线AB与平面a的 位置关系为() A.AB⊥a B.ABCa C.AB与a相交不垂直 D.AB∥a 解析:nAE=(2,-2,4)(-3,1,2)=-6-2+8=0,∴.n⊥AB.又点A不在a内,∴AB∥a 答案D 4.如图,在长方体ABCD-A1B1C1D1中,B1C和C1D与底面所成的角分别为60°和45°,则异面直 线B1C和CD所成角的余弦值为( A哈 B哈 D 答案:A 5.在空间直角坐标系中,棱长为2的正方体ABCD-A1B1CD1如图所示,若E,F分别是BC,DD1 的中点,则EF的坐标为
复习课 1.空间向量与立体几何 基础巩固 1.在空间四边形 ABCD 中,连接 AC,BD,若△BCD 是正三角形,且 E 为其中心,则𝐴𝐵⃗⃗⃗ + 1 2 𝐵𝐶⃗⃗⃗ − 3 2 𝐷𝐸⃗⃗⃗⃗ − 𝐴𝐷⃗⃗⃗⃗ 的化简结果为( ) A.𝐴𝐵⃗⃗⃗ B.2𝐵𝐷⃗ ⃗ C.0 D.2𝐷𝐸⃗⃗⃗⃗ 解析:如图,设 BC 的中点为 F,E 是 DF 的三等分点, ∴ 3 2 𝐷𝐸⃗⃗⃗⃗ = 𝐷𝐹⃗⃗⃗ , ∴ 1 2 𝐵𝐶⃗⃗⃗ = 𝐵𝐹⃗⃗⃗ ,∴𝐴𝐵⃗⃗⃗ + 1 2 𝐵𝐶⃗⃗⃗ − 3 2 𝐷𝐸⃗⃗⃗⃗ − 𝐴𝐷⃗⃗⃗⃗ = 𝐴𝐵⃗⃗⃗ + 𝐵𝐹⃗⃗⃗ − 𝐷𝐹⃗⃗⃗ − 𝐴𝐷⃗⃗⃗⃗ = 𝐴𝐹⃗⃗⃗ + 𝐹𝐷⃗⃗⃗ − 𝐴𝐷⃗⃗⃗⃗ = 𝐴𝐷⃗⃗⃗⃗ − 𝐴𝐷⃗⃗⃗⃗ =0. 答案:C 2.已知 a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若 a,b,c 三向量共面,则实数 λ 等于( ) A.62 7 B.63 7 C.64 7 D.65 7 解析:若 a,b,c 三向量共面,则存在 x,y 使 c=xa+yb, 即{ 7 = 2𝑥-𝑦, 5 = -𝑥 + 4𝑦, 𝜆 = 3𝑥-2𝑦, 解得 λ= 65 7 .故选 D. 答案:D 3.已知平面 α 的一个法向量为 n=(2,-2,4),𝐴𝐵⃗⃗⃗ =(-3,1,2),点 A 不在 α 内,则直线 AB 与平面 α 的 位置关系为( ) A.AB⊥α B.AB⊂α C.AB 与 α 相交不垂直 D.AB∥α 解析:∵n·𝐴𝐵⃗⃗⃗ =(2,-2,4)·(-3,1,2)=-6-2+8=0,∴n⊥𝐴𝐵⃗⃗⃗ .又点 A 不在 α 内,∴AB∥α. 答案:D 4.如图,在长方体 ABCD-A1B1C1D1 中,B1C 和 C1D 与底面所成的角分别为 60°和 45°,则异面直 线 B1C 和 C1D 所成角的余弦值为( ) A.√6 4 B.√6 3 C.√2 6 D.√2 3 答案:A 5.在空间直角坐标系中,棱长为 2 的正方体 ABCD-A1B1C1D1 如图所示,若 E,F 分别是 BC,DD1 的中点,则𝐸𝐹⃗⃗ 的坐标为
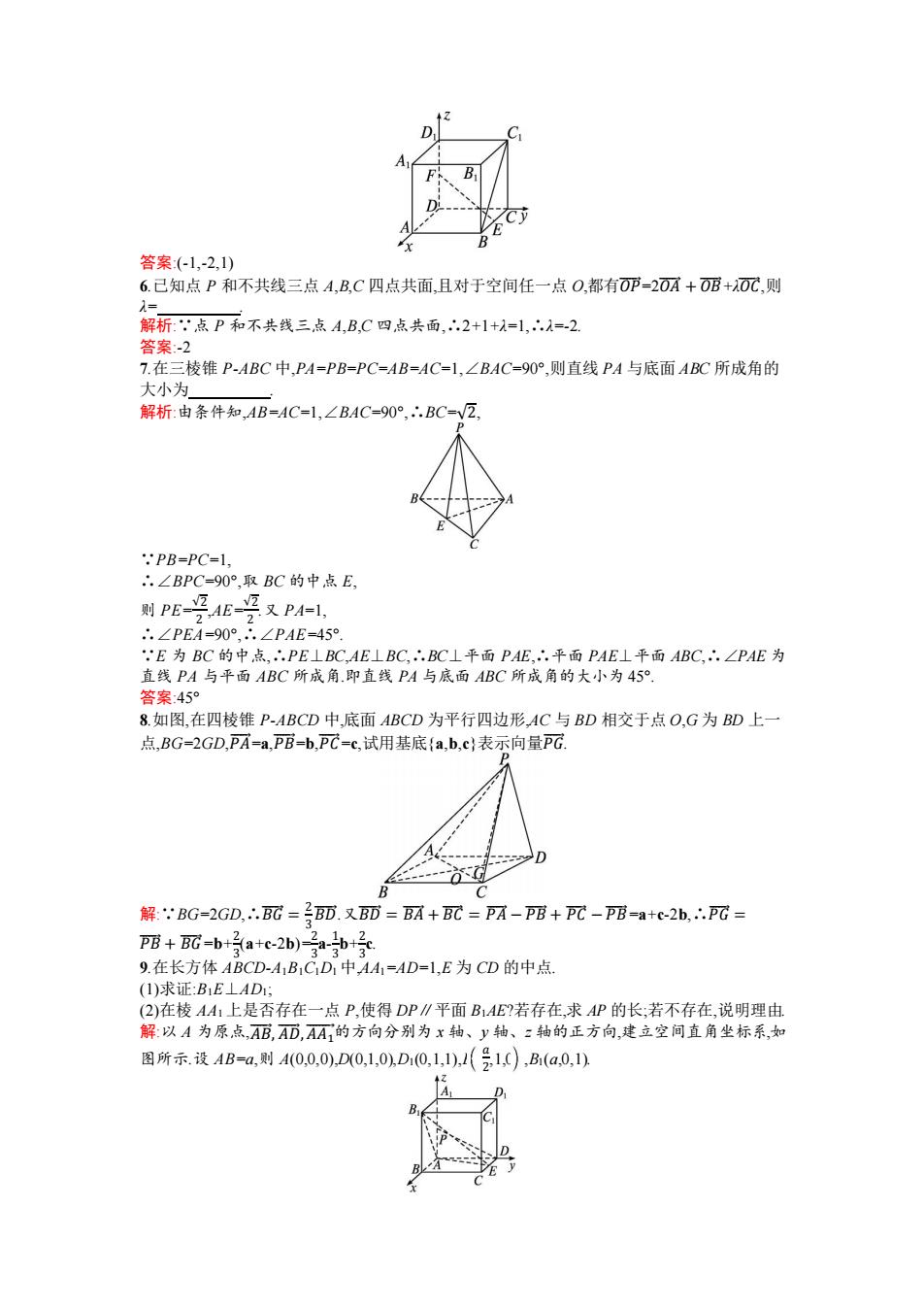
A B Cy A 答案(-1,-2,1) 6.己知点P和不共线三点A,B,C四点共面,且对于空间任一点O,都有丽-20A+0丽+0C,则 λ= 解析:点P和不共线三点A,B,C四点共面,2+1+1=1,∴1=-2 答案-2 7.在三棱锥P-ABC中,PA=PB=PC=AB=AC=1,∠BAC-90°,则直线PA与底面ABC所成角的 大小为 解析:由条件知,AB=AC-1,∠BAC=90°,∴.BC=√Z, .PB=PC=1, ∴.∠BPC=90°,取BC的中点E, 则PE-受AE-要又PA1, ∴.∠PEA=90°,.∠PAE=45° E为BC的中点,∴PE⊥BC,AE⊥BC,∴.BC⊥平面PAE,∴.平面PAE⊥平面ABC,∴.∠PAE为 直线PA与平面ABC所成角.即直线PA与底面ABC所成角的大小为45° 答案:45° 8.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AC与BD相交于点O,G为BD上一 点,BG=2GD,PA=a,PB=b,PC=c,试用基底{a,b,c}表示向量PC. D 解BG=2GD,∴.BC=二BD.又BD=BA+BC=PA-PB+P-PB=a+c-2b,∴PG= P+C=-b+a+c2b)号ab+号 9.在长方体ABCD-A1B1CD1中,AA1=AD=1,E为CD的中点, (1)求证:B1E⊥AD1; (2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由. 解:以A为原点,AB,AD,AA的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,如 图所示.设AB=a,则400,0),D01,0,D10,11),1(1,C),B1(a0,1
答案:(-1,-2,1) 6.已知点 P 和不共线三点 A,B,C 四点共面,且对于空间任一点 O,都有𝑂𝑃⃗⃗⃗ =2𝑂𝐴⃗⃗⃗ + 𝑂𝐵⃗⃗⃗⃗ +λ⃗𝑂𝐶⃗⃗ ,则 λ= . 解析:∵点 P 和不共线三点 A,B,C 四点共面,∴2+1+λ=1,∴λ=-2. 答案:-2 7.在三棱锥 P-ABC 中,PA=PB=PC=AB=AC=1,∠BAC=90°,则直线 PA 与底面 ABC 所成角的 大小为 . 解析:由条件知,AB=AC=1,∠BAC=90°,∴BC=√2, ∵PB=PC=1, ∴∠BPC=90°,取 BC 的中点 E, 则 PE=√2 2 ,AE=√2 2 .又 PA=1, ∴∠PEA=90°,∴∠PAE=45°. ∵E 为 BC 的中点,∴PE⊥BC,AE⊥BC,∴BC⊥平面 PAE,∴平面 PAE⊥平面 ABC,∴∠PAE 为 直线 PA 与平面 ABC 所成角.即直线 PA 与底面 ABC 所成角的大小为 45°. 答案:45° 8.如图,在四棱锥 P-ABCD 中,底面 ABCD 为平行四边形,AC 与 BD 相交于点 O,G 为 BD 上一 点,BG=2GD,𝑃𝐴⃗⃗⃗ =a,𝑃𝐵⃗⃗⃗ =b,𝑃𝐶⃗⃗ =c,试用基底{a,b,c}表示向量𝑃𝐺⃗⃗⃗ . 解:∵BG=2GD,∴𝐵𝐺⃗⃗⃗ = 2 3 𝐵𝐷⃗ ⃗ .又𝐵𝐷⃗ ⃗ = 𝐵𝐴⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ = 𝑃𝐴⃗⃗⃗ − 𝑃𝐵⃗⃗⃗ + 𝑃𝐶⃗⃗ − 𝑃𝐵⃗⃗⃗ =a+c-2b,∴𝑃𝐺⃗⃗⃗ = 𝑃𝐵⃗⃗⃗ + 𝐵𝐺⃗⃗⃗ =b+ 2 3 (a+c-2b)= 2 3 a- 1 3 b+ 2 3 c. 9.在长方体 ABCD-A1B1C1D1 中,AA1=AD=1,E 为 CD 的中点. (1)求证:B1E⊥AD1; (2)在棱 AA1 上是否存在一点 P,使得 DP∥平面 B1AE?若存在,求 AP 的长;若不存在,说明理由. 解:以 A 为原点,𝐴𝐵⃗⃗⃗ , 𝐴𝐷⃗⃗⃗⃗ ,𝐴𝐴1 ⃗⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴的正方向,建立空间直角坐标系,如 图所示.设 AB=a,则 A(0,0,0),D(0,1,0),D1(0,1,1),E 𝑎 2 ,1,0 ,B1(a,0,1)

(1)证明:AD1-(0,1,1),B1E-(-号1,1),因为AD1·B1E-号×0+1×1+(-1)×1-0,所以B1E⊥AD1 (2)假设在棱A41上存在一点P(0,0,20),使得DP∥平面B1AE,此时D严=(0,-1,0). 设平面B1AE的法向量为n=(xJy,=). 因为nL平面BE,=a0,1)正-号1,0,所以nLAB LZ正,得ng二+z=0 {mA正=%+y=0, 取x=l,得平面B1AE的一个法向量n=(1,号-a,要使DP∥平面BAE,只需nLDP,有兰a=0, 解得0之所以AP二所以在棱A41上存在点P,使得DP∥平面BME且P为A4的中点 拓展提高 1.如图,在直二面角a-1-B中,A,B∈I,ACCa,AC⊥1,BDCB,BD⊥I,AC=6,AB=8,BD=24,则线段CD 的长是( A.25 B.26 C.27 D.28 解析:AC⊥AB,BDLAB,.∴.AC.AB=0,BD,AB-0,AC.BD=0,CD=CA+AB+BD CD=|CA+AB+BD2-676,.CD1=26 答案B 2.在矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使点A在平面BCD内的射影落 在边BC上.若二面角C-AB-D的平面角大小为0,则sinO的值等于() A B C.3 7 D 解析:如图,'AO⊥平面BCD,AO⊥CD.又CD⊥BC,.CD⊥平面ABC,DA⊥AB,AC是AD在 平面ABC上的射影,∴AC⊥AB,∠DAC为二面角C-AB-D的平面角. 在Rt△ACD中,CD-3,AD=4,则sin∠DAC=sin0- 答案:A 3.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB的中点,则点E到平面 ACD1的距离为() 号 B 2 c D 解析:如图,以D为坐标原点,DA,D元,DD的方向分别为x轴、y轴、:轴正方向,建立空间直 角坐标系,则D(0,0,1),E1,1,0),A(1,0,0),C0,2,0).从而D1E=(1,1,-1),AC=(-1,2,0),AD1=(-1,0,1)
(1)证明:𝐴𝐷1 ⃗⃗⃗⃗⃗ =(0,1,1),𝐵⃗⃗ 1 ⃗⃗𝐸 =(- 𝑎 2 ,1,-1),因为𝐴𝐷1 ⃗⃗⃗⃗⃗ · 𝐵⃗⃗ 1 ⃗⃗𝐸 =- 𝑎 2 ×0+1×1+(-1)×1=0,所以 B1E⊥AD1. (2)假设在棱 AA1 上存在一点 P(0,0,z0),使得 DP∥平面 B1AE,此时𝐷𝑃⃗⃗⃗ =(0,-1,z0). 设平面 B1AE 的法向量为 n=(x,y,z). 因为 n⊥平面 B1AE,𝐴𝐵1 ⃗⃗⃗⃗⃗ =(a,0,1),𝐴𝐸⃗⃗⃗ =( 𝑎 2 ,1,0),所以 n⊥𝐴𝐵1 ⃗⃗⃗⃗⃗ ,n⊥𝐴𝐸⃗⃗⃗ ,得{ 𝑛·𝐴𝐵1 ⃗⃗⃗⃗⃗ = 𝑎𝑥 + 𝑧 = 0, 𝑛·𝐴𝐸⃗⃗⃗ = 𝑎𝑥 2 + 𝑦 = 0, 取 x=1,得平面 B1AE 的一个法向量 n=(1,- 𝑎 2 ,-a),要使 DP∥平面 B1AE,只需 n⊥𝐷𝑃⃗⃗⃗ ,有 𝑎 2 -az0=0, 解得 z0= 1 2 .所以 AP=1 2 ,所以在棱 AA1 上存在点 P,使得 DP∥平面 B1AE,且 P 为 AA1 的中点. 拓展提高 1.如图,在直二面角 α-l-β 中,A,B∈l,AC⊂α,AC⊥l,BD⊂β,BD⊥l,AC=6,AB=8,BD=24,则线段 CD 的长是( ) A.25 B.26 C.27 D.28 解析:∵AC⊥AB,BD⊥AB,∴𝐴𝐶⃗⃗ · 𝐴𝐵⃗⃗⃗ =0,𝐵𝐷⃗ ⃗ · 𝐴𝐵⃗⃗⃗ =0,𝐴𝐶⃗⃗ · 𝐵𝐷⃗ ⃗ =0,𝐶𝐷⃗⃗⃗ = 𝐶𝐴⃗⃗ + 𝐴𝐵⃗⃗⃗ + 𝐵𝐷⃗ ⃗ ,∴ |𝐶𝐷⃗⃗⃗ | 2=|𝐶𝐴⃗⃗ + 𝐴𝐵⃗⃗⃗ + 𝐵𝐷⃗ ⃗ | 2=676,∴|𝐶𝐷⃗⃗⃗ |=26. 答案:B 2.在矩形 ABCD 中,AB=3,BC=4,沿对角线 BD 将△ABD 折起,使点 A 在平面 BCD 内的射影落 在边 BC 上.若二面角 C-AB-D 的平面角大小为 θ,则 sin θ 的值等于( ) A.3 4 B.√7 4 C.3√7 7 D.4 5 解析:如图,∵AO⊥平面 BCD,∴AO⊥CD.又 CD⊥BC,∴CD⊥平面 ABC,DA⊥AB,AC 是 AD 在 平面 ABC 上的射影,∴AC⊥AB,∠DAC 为二面角 C-AB-D 的平面角. 在 Rt△ACD 中,CD=3,AD=4,则 sin∠DAC=sin θ= 3 4 . 答案:A 3.如图,在长方体 ABCD-A1B1C1D1 中,AD=AA1=1,AB=2,点 E 是棱 AB 的中点,则点 E 到平面 ACD1 的距离为( ) A.1 2 B.√2 2 C.1 3 D.1 6 解析:如图,以 D 为坐标原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直 角坐标系,则 D1(0,0,1),E(1,1,0),A(1,0,0),C(0,2,0).从而𝐷⃗⃗⃗ 1 ⃗𝐸⃗ =(1,1,-1),𝐴𝐶⃗⃗ =(-1,2,0),𝐴𝐷1 ⃗⃗⃗⃗⃗ =(-1,0,1)

设平面ACD1的法向量为n=(a,b,c), 则n4C=a+2b=0, (n:AD1=-a+c=0, 令a2则n212所以点E到平面4CD,的距离为a-号 答案C 4.己知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上当∠APC最大时,三棱锥P-ABC 的体积为) A云 B古 c D立 解析:以B为坐标原点,BA,B配,BB的方向分别为x轴、y轴、:轴正方向,建立空间直角坐标 系,如图所示, 设即-BD,可得PU,1,再由cos阿受可求得当时,cosm元>的值最小 PAP元 即∠APC最大,故puc×Ix1写=品故选B 答案B 5.将正方形ABCD沿对角线BD折成直二面角,给出下列四个结论:①AC⊥BD,②AB,CD所成 角为60°:③△ADC为等边三角形:,④AB与平面BCD所成角为60°.其中正确的结论 是 (请将你认为是正确结论的序号都填上) 答案:①②③ 6.如图所示,在正四棱柱ABCD-A1B1CD1中,已知AB=2AA1=5,EF分别为D1DB1B上的点且 DE=B F=1. A B (1)求证:BE⊥平面ACF, (2)求点E到平面ACF的距离. (I)证明:以D为原点,DA,DC,DD1的方向分别为x轴、y轴、:轴正方向,建立空间直角坐标 系,如图所示 D 则D(0,0,0),A(2,0,0),B2,2,0),C(0,2,0),D1(0,0,5),E0,0,1),F22,4) ∴.AC-(-2,2,0),AF-(0,2,4),BE-(-2,-2,1),AE=(-2,0,1) BE.AC-0,BE.AF=O,∴.BE⊥AC,BE⊥AF,且ACOAF=A. ,.BE⊥平面ACF」
设平面 ACD1 的法向量为 n=(a,b,c), 则{ 𝑛·𝐴𝐶⃗⃗ = -𝑎 + 2𝑏 = 0, 𝑛·𝐴𝐷1 ⃗⃗⃗⃗⃗ = -𝑎 + 𝑐 = 0, 令 a=2,则 n=(2,1,2).所以点 E 到平面 ACD1 的距离为 d=|𝐷⃗⃗⃗⃗ 1 ⃗⃗⃗𝐸⃗ ·𝑛| |𝑛| = 1 3 . 答案:C 4.已知正方体 ABCD-A1B1C1D1 棱长为 1,点 P 在线段 BD1 上.当∠APC 最大时,三棱锥 P-ABC 的体积为( ) A. 1 24 B. 1 18 C.1 9 D. 1 12 解析:以 B 为坐标原点,𝐵𝐴⃗⃗⃗ ,𝐵𝐶⃗⃗⃗ , 𝐵𝐵1 ⃗⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标 系,如图所示, 设𝐵𝑃⃗⃗⃗ =λ𝐵𝐷1 ⃗⃗ ⃗⃗ ,可得 P(λ,λ,λ),再由 cos=𝑃𝐴⃗⃗⃗⃗⃗ ·𝑃𝐶⃗⃗⃗⃗ |𝑃𝐴⃗⃗⃗⃗⃗ ||𝑃𝐶⃗⃗⃗⃗ | ,可求得当 λ= 1 3 时,cos的值最小, 即∠APC 最大,故 VP-ABC= 1 3 × 1 2 ×1×1×1 3 = 1 18.故选 B. 答案:B 5.将正方形 ABCD 沿对角线 BD 折成直二面角,给出下列四个结论:①AC⊥BD;②AB,CD 所成 角为 60°;③△ADC 为等边三角形;④AB 与平面 BCD 所成角为 60°.其中正确的结论 是 .(请将你认为是正确结论的序号都填上) 答案:①②③ 6.如图所示,在正四棱柱 ABCD-A1B1C1D1 中,已知 AB=2,AA1=5,E,F 分别为 D1D,B1B 上的点,且 DE=B1F=1. (1)求证:BE⊥平面 ACF; (2)求点 E 到平面 ACF 的距离. (1)证明:以 D 为原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标 系,如图所示. 则 D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),D1(0,0,5),E(0,0,1),F(2,2,4). ∴𝐴𝐶⃗⃗ =(-2,2,0),𝐴𝐹⃗⃗⃗ =(0,2,4),𝐵𝐸⃗⃗⃗ =(-2,-2,1),𝐴𝐸⃗⃗⃗ =(-2,0,1). ∵𝐵𝐸⃗⃗⃗ · 𝐴𝐶⃗⃗ =0,𝐵𝐸⃗⃗⃗ · 𝐴𝐹⃗⃗⃗ =0,∴BE⊥AC,BE⊥AF,且 AC∩AF=A. ∴BE⊥平面 ACF

(2)解:由(1)知,BE为平面AC℉的一个法向量, 点E到平西ACF的距离d西要-号 BE 故点E到平面ACF的距离为码 挑战创新 如图,在直三棱柱ABC-A'B'C中,∠B4C=90°,AB=AC=LAA',点M,N分别为A'B和B'C的中点. 4 B (1)求证:MN∥平面A'ACC, (2)若二面角A'-MN-C为直二面角,求1的值. (1)证明:如图,连接AB',AC',由已知∠BAC-90°,AB=AC,三棱柱ABC-A'B'C为直三棱柱,所以M 为AB的中点 又因为N为B'C的中点,所以MN∥AC:又MN4平面A'ACC',ACc平面A'ACC,因此MN∥平 面AACC Z↑A' (2)解:以A为坐标原点,以AB,AC,AA的方向为x轴、y轴、z轴正方向,建立空间直角坐标系 A灯,如图所示 设AA'=1,则AB=AC=1,于是A0,0,0),B(1,0,0),C(01,0),A0,0,1),B(2,0,1),C(0,2,1), 所以M(0》(经 设m=(x1,n,1)是平面A'MN的法向量, mW=2x1-21=0, 1 则 可取m=(1,-1,). mMm=2h+2z1=0 设n=(22,2)是平面MNC的法向量, nNc=-2x2+22-22=0 则 nMW=2y2+2=0, 可取n=(-3,-1,).因为二面角A-MN-C为直二面角,所以 mn=0,即-3+(-1)×(-1)+2-0,解得1=V2(负值舍去)
(2)解:由(1)知,𝐵𝐸⃗⃗⃗ 为平面 ACF 的一个法向量, ∴点 E 到平面 ACF 的距离 d=|𝐴𝐸⃗⃗⃗⃗⃗ ·𝐵𝐸⃗⃗⃗⃗⃗ | |𝐵𝐸⃗⃗⃗⃗⃗ | = 5 3 . 故点 E 到平面 ACF 的距离为5 3 . 挑战创新 如图,在直三棱柱 ABC-A'B'C'中,∠BAC=90°,AB=AC=λAA',点 M,N 分别为 A'B 和 B'C'的中点. (1)求证:MN∥平面 A'ACC'; (2)若二面角 A'-MN-C 为直二面角,求 λ 的值. (1)证明:如图,连接 AB',AC',由已知∠BAC=90°,AB=AC,三棱柱 ABC-A'B'C'为直三棱柱,所以 M 为 AB'的中点. 又因为 N 为 B'C'的中点,所以 MN∥AC'.又 MN⊄平面 A'ACC',AC'⊂平面 A'ACC',因此 MN∥平 面 A'ACC'. (2)解:以 A 为坐标原点,以𝐴𝐵⃗⃗⃗ ,𝐴𝐶⃗⃗ ,𝐴𝐴⃗⃗⃗ '的方向为 x 轴、y 轴、z 轴正方向,建立空间直角坐标系 Axyz,如图所示. 设 AA'=1,则 AB=AC=λ,于是 A(0,0,0),B(λ,0,0),C(0,λ,0),A'(0,0,1),B'(λ,0,1),C'(0,λ,1), 所以 M 𝜆 2 ,0,1 2 ,N 𝜆 2 , 𝜆 2 ,1 . 设 m=(x1,y1,z1)是平面 A'MN 的法向量, 则{ 𝑚·𝐴⃗⃗'⃗𝑀⃗ = 𝜆 2 𝑥1 - 1 2 𝑧1 = 0, 𝑚·𝑀𝑁⃗⃗⃗ = 𝜆 2 𝑦1 + 1 2 𝑧1 = 0, 可取 m=(1,-1,λ). 设 n=(x2,y2,z2)是平面 MNC 的法向量, 则{ 𝑛·𝑁𝐶⃗⃗⃗⃗ = - 𝜆 2 𝑥2 + 𝜆 2 𝑦2 -𝑧2 = 0, 𝑛·𝑀𝑁⃗⃗⃗ = 𝜆 2 𝑦2 + 1 2 𝑧2 = 0, 可取 n=(-3,-1,λ).因为二面角 A'-MN-C 为直二面角,所以 m·n=0,即-3+(-1)×(-1)+λ 2=0,解得 λ=√2(负值舍去)