
1.2空间向量在立体几何中的应用 1.2.1空间中的点、直线与空间向量 1.已知两条不重合直线1和h的方向向量分别为v1=(1,0,-1),V2=(-2,0,2),则h与h的位置关 系是( A.平行 B.相交 C.垂直 D.不确定 解析:v2=-2v1,∴V1∥v2,∴.h1∥2 答案:A 2.己知两向量v1=(2,0,3),V2=(-3,0,2),则以向量v1,V2为方向向量的直线1,2的夹角为() A.90° B.45° C.60° D.30° -6+6 解析:Cos=V3x0, ∴v1⊥V2,.h1h. 答案:A 3.已知A,B,C三点的坐标分别为A(4,1,3),B2,-5,1),C3,7),若AB⊥AC,则1等于() A.28 B.-28 C.14 D.-14 解析:AE=(-2,-6,-2),AC=(-1,6,1-3), .AE.AC=2-36-2(1-3)=0,∴.1=-14 答案D 4.如图,在正方体ABCD-A1B1CD1中,E,F,G,H分别是A41,AB,BB1,BC的中点,则异面直线EF 与GH所成的角等于() A.45° B.60° C.90° D.30° 解析:以D为原点,DA,DC,DD的方向分别为x轴、y轴、z轴正方向,建立空间直角坐标系, 如图所示 设正方体的棱长为1,则E(1,0,2,F(1,20),G(1,12H1,1),即F=(0,2).丽=( 0引oF,0丽孕故选B 答案B 5.(多选题)在正方体ABCD-A1B1C1D1中,E为A1C1的中点,则下列直线与直线CE垂直的是 () A.AC B.BD C.BiD D.A1A 答案BC 6.己知两条异面直线a,b的夹角为80°,a,b分别为直线a,b的方向向量,则 = 答案:80°或100°
1.2 空间向量在立体几何中的应用 1.2.1 空间中的点、直线与空间向量 1.已知两条不重合直线 l1 和 l2 的方向向量分别为 v1=(1,0,-1),v2=(-2,0,2),则 l1 与 l2 的位置关 系是( ) A.平行 B.相交 C.垂直 D.不确定 解析:∵v2=-2v1,∴v1∥v2,∴l1∥l2. 答案:A 2.已知两向量 v1=(2,0,3),v2=(-3,0,2),则以向量 v1,v2 为方向向量的直线 l1,l2 的夹角为( ) A.90° B.45° C.60° D.30° 解析:∵cos= -6+6 √13×√13=0, ∴v1⊥v2,∴l1⊥l2. 答案:A 3.已知 A,B,C 三点的坐标分别为 A(4,1,3),B(2,-5,1),C(3,7,λ),若𝐴𝐵⃗⃗⃗ ⊥ 𝐴𝐶⃗⃗ ,则 λ 等于( ) A.28 B.-28 C.14 D.-14 解析:∵𝐴𝐵⃗⃗⃗ =(-2,-6,-2),𝐴𝐶⃗⃗ =(-1,6,λ-3), ∴𝐴𝐵⃗⃗⃗ · 𝐴𝐶⃗⃗ =2-36-2(λ-3)=0,∴λ=-14. 答案:D 4.如图,在正方体 ABCD-A1B1C1D1 中,E,F,G,H 分别是 AA1,AB,BB1,B1C1 的中点,则异面直线 EF 与 GH 所成的角等于( ) A.45° B.60° C.90° D.30° 解析:以 D 为原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标系, 如图所示. 设正方体的棱长为 1,则 E(1,0,1 2 ),F(1, 1 2 ,0),G(1,1,1 2 ),H( 1 2 ,1,1),即𝐸𝐹⃗⃗ = (0, 1 2 ,- 1 2 ) ,𝐺𝐻⃗ ⃗ = (- 1 2 ,0, 1 2 ),cos= - 1 4 √2 2 × √2 2 =- 1 2 .故选 B. 答案:B 5.(多选题)在正方体 ABCD-A1B1C1D1 中,E 为 A1C1 的中点,则下列直线与直线 CE 垂直的是 ( ) A.AC B.BD C.B1D1 D.A1A 答案:BC 6.已知两条异面直线 a,b 的夹角为 80°,a,b 分别为直线 a,b 的方向向量,则 = . 答案:80°或 100°
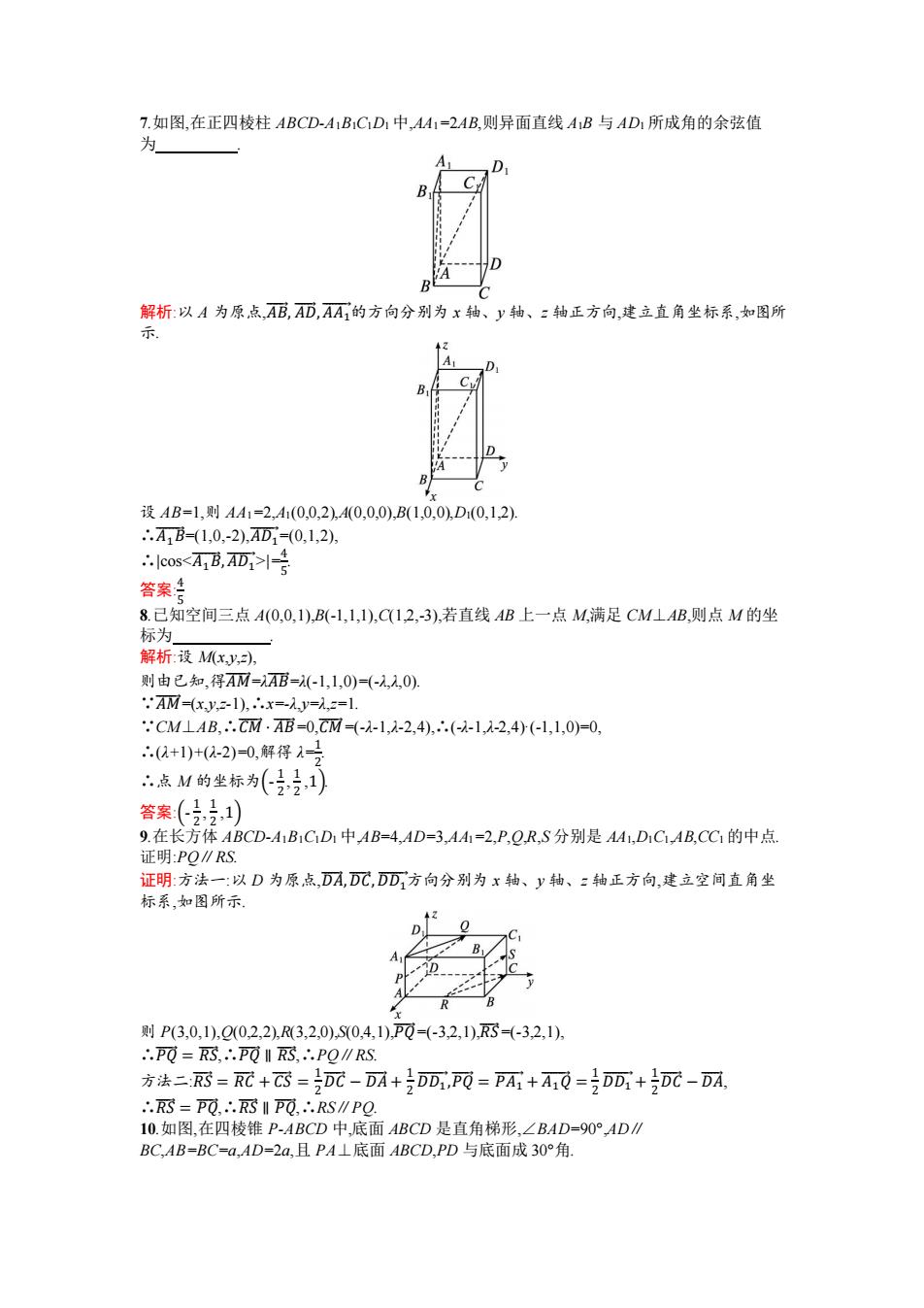
7.如图,在正四棱柱ABCD-A1B1CD1中,A41=2AB,则异面直线AB与AD1所成角的余弦值 为■ D B 解析:以A为原点,AB,AD,AA的方向分别为x轴、y轴、z轴正方向,建立直角坐标系,如图所 示 B B 设AB=1,则AA1=2,A(0,0,2),A(0,0,0),B(1,0,0),D1(0,1,2). .A1B=(1,0,-2),AD=(0,1,2), ∴lcos1号 答案生 8.已知空间三点A(0,0,1),B(-1,1,1),C(1,2,-3),若直线AB上一点M,满足CMLAB,则点M的坐 标为 解析:设Mx,y,), 则由已知,得AM=AB=(-1,1,0)=(-1,1,0) AM=(xy,-l),∴x=-1y=1,2=1. .CMLAB,.CM.AE=0,CM-(-1-1,-2,4),∴.(-1,1-2,4)(-1,1,0)=0, ∴(+1)+0-2)=0,解得1-号 “点M的坐标为(,1) 答案(21) 9.在长方体ABCD-A1B1C1D1中,AB=4,AD=3,A4=2,P,Q,R,S分别是A41,D1C,AB,CC1的中点. 证明:PO∥RS. 证明:方法一:以D为原点,DA,DC,DD方向分别为x轴、y轴、二轴正方向,建立空间直角坐 标系,如图所示 则P(3,0,1),Q0,2,2),R3,2,0),S0,4,1),P0=(-3,2,1),=(-3,2,1) ∴.PO=,∴.P0‖,∴PQ∥S 方法二丽-C+=DC-DA+2DD,P0-PA1+A10=DD+D元-DA .=P0,.IP0,RS∥PQ 10.如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥ BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角
7.如图,在正四棱柱 ABCD-A1B1C1D1 中,AA1=2AB,则异面直线 A1B 与 AD1 所成角的余弦值 为 . 解析:以 A 为原点,𝐴𝐵⃗⃗⃗ , 𝐴𝐷⃗⃗⃗⃗ ,𝐴𝐴1 ⃗⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立直角坐标系,如图所 示. 设 AB=1,则 AA1=2,A1(0,0,2),A(0,0,0),B(1,0,0),D1(0,1,2). ∴𝐴⃗⃗⃗ 1 ⃗⃗𝐵 =(1,0,-2),𝐴𝐷1 ⃗⃗⃗⃗⃗ =(0,1,2), ∴|cos|=4 5 . 答案: 4 5 8.已知空间三点 A(0,0,1),B(-1,1,1),C(1,2,-3),若直线 AB 上一点 M,满足 CM⊥AB,则点 M 的坐 标为 . 解析:设 M(x,y,z), 则由已知,得𝐴𝑀⃗⃗⃗⃗ =λ𝐴𝐵⃗⃗⃗ =λ(-1,1,0)=(-λ,λ,0). ∵𝐴𝑀⃗⃗⃗⃗ =(x,y,z-1),∴x=-λ,y=λ,z=1. ∵CM⊥AB,∴𝐶𝑀⃗⃗⃗ · 𝐴𝐵⃗⃗⃗ =0,𝐶𝑀⃗⃗⃗ =(-λ-1,λ-2,4),∴(-λ-1,λ-2,4)·(-1,1,0)=0, ∴(λ+1)+(λ-2)=0,解得 λ= 1 2 . ∴点 M 的坐标为(- 1 2 , 1 2 ,1). 答案:(- 1 2 , 1 2 ,1) 9.在长方体 ABCD-A1B1C1D1 中,AB=4,AD=3,AA1=2,P,Q,R,S 分别是 AA1,D1C1,AB,CC1 的中点. 证明:PQ∥RS. 证明:方法一:以 D 为原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐 标系,如图所示. 则 P(3,0,1),Q(0,2,2),R(3,2,0),S(0,4,1),𝑃𝑄⃗⃗⃗ =(-3,2,1),𝑅𝑆⃗ =(-3,2,1), ∴𝑃𝑄⃗⃗⃗ = 𝑅𝑆⃗ ,∴𝑃𝑄⃗⃗⃗ ∥ 𝑅𝑆⃗ ,∴PQ∥RS. 方法二:𝑅𝑆⃗ = 𝑅𝐶⃗⃗ +⃗𝐶𝑆⃗⃗ = 1 2 𝐷𝐶⃗⃗⃗ − 𝐷𝐴⃗⃗⃗⃗ + 1 2 𝐷𝐷1 ⃗⃗⃗⃗ ,𝑃𝑄⃗⃗⃗ = 𝑃𝐴1 ⃗⃗⃗⃗⃗ + 𝐴⃗⃗ 1 ⃗𝑄 = 1 2 𝐷𝐷1 ⃗⃗⃗⃗ + 1 2 𝐷𝐶⃗⃗⃗ − 𝐷𝐴⃗⃗⃗⃗ , ∴𝑅𝑆⃗ = 𝑃𝑄⃗⃗⃗ ,∴𝑅𝑆⃗ ∥ 𝑃𝑄⃗⃗⃗ ,∴RS∥PQ. 10.如图,在四棱锥 P-ABCD 中,底面 ABCD 是直角梯形,∠BAD=90°,AD∥ BC,AB=BC=a,AD=2a,且 PA⊥底面 ABCD,PD 与底面成 30°角

(1)若AE⊥PD,E为垂足,求证:BE⊥PD (2)求异面直线AE与CD所成角的大小(用反三角函数表示) (I)证明:,PA⊥底面ABCD,∴PALAB. 又AB⊥AD,AB⊥平面PAD,AB⊥PD 又AE⊥PD,∴PD⊥平面ABE,∴BE⊥PD (2)解:如图,以A为原点,AB,AD,AP所在方向分别为x轴、y轴、:轴正方向,建立空间直角坐 标系,则点C,D的坐标分别为(a,a,0),(0,2a,0) ,PA⊥底面ABCD, ∠PDA是PD与底面ABCD所成的角, ∴.∠PDA=30 于是,在Rt△AED中,由AD=2a,得AE=a. 过点E作EFLAD,叁足为点E在R△AFE中,由ABa,∠EAF-60,°得A-之EF- 0 于是,正=(o,a号a),西-(aa,0 设A正与C而的夹角为0, 则cos0-亚西 AEICD 0(-aj+2a+9a0 0++ (-a2+a2+02 ∴.0=arccos4 ∴.AE与CD所成角的大小为arccos-4
(1)若 AE⊥PD,E 为垂足,求证:BE⊥PD; (2)求异面直线 AE 与 CD 所成角的大小(用反三角函数表示). (1)证明:∵PA⊥底面 ABCD,∴PA⊥AB. 又 AB⊥AD,∴AB⊥平面 PAD,∴AB⊥PD. 又 AE⊥PD,∴PD⊥平面 ABE,∴BE⊥PD. (2)解:如图,以 A 为原点,𝐴𝐵⃗⃗⃗ ,𝐴𝐷⃗⃗⃗⃗ , 𝐴𝑃⃗⃗⃗ 所在方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐 标系,则点 C,D 的坐标分别为(a,a,0),(0,2a,0). ∵PA⊥底面 ABCD, ∴∠PDA 是 PD 与底面 ABCD 所成的角, ∴∠PDA=30°. 于是,在 Rt△AED 中,由 AD=2a,得 AE=a. 过点 E 作 EF⊥AD,垂足为点 F,在 Rt△AFE 中,由 AE=a,∠EAF=60°,得 AF=1 2 a,EF=√3 2 a, ∴E(0,1 2 a, √3 2 a). 于是,𝐴𝐸⃗⃗⃗ = (0, 1 2 𝑎, √3 2 𝑎) , 𝐶𝐷⃗⃗⃗ =(-a,a,0). 设𝐴𝐸⃗⃗⃗ 与𝐶𝐷⃗⃗⃗ 的夹角为 θ, 则 cos θ= 𝐴𝐸⃗⃗⃗⃗⃗ ·𝐶𝐷⃗⃗⃗⃗⃗ |𝐴𝐸⃗⃗⃗⃗⃗ ||𝐶𝐷⃗⃗⃗⃗⃗ | = 0·(-𝑎)+ 1 2 𝑎·𝑎+ √3 2 𝑎·0 √0 2+( 1 2 𝑎) 2 +( √3 2 𝑎) 2 ·√(-𝑎) 2+𝑎2+0 2 = √2 4 , ∴θ=arccos √2 4 , ∴AE 与 CD 所成角的大小为 arccos √2 4