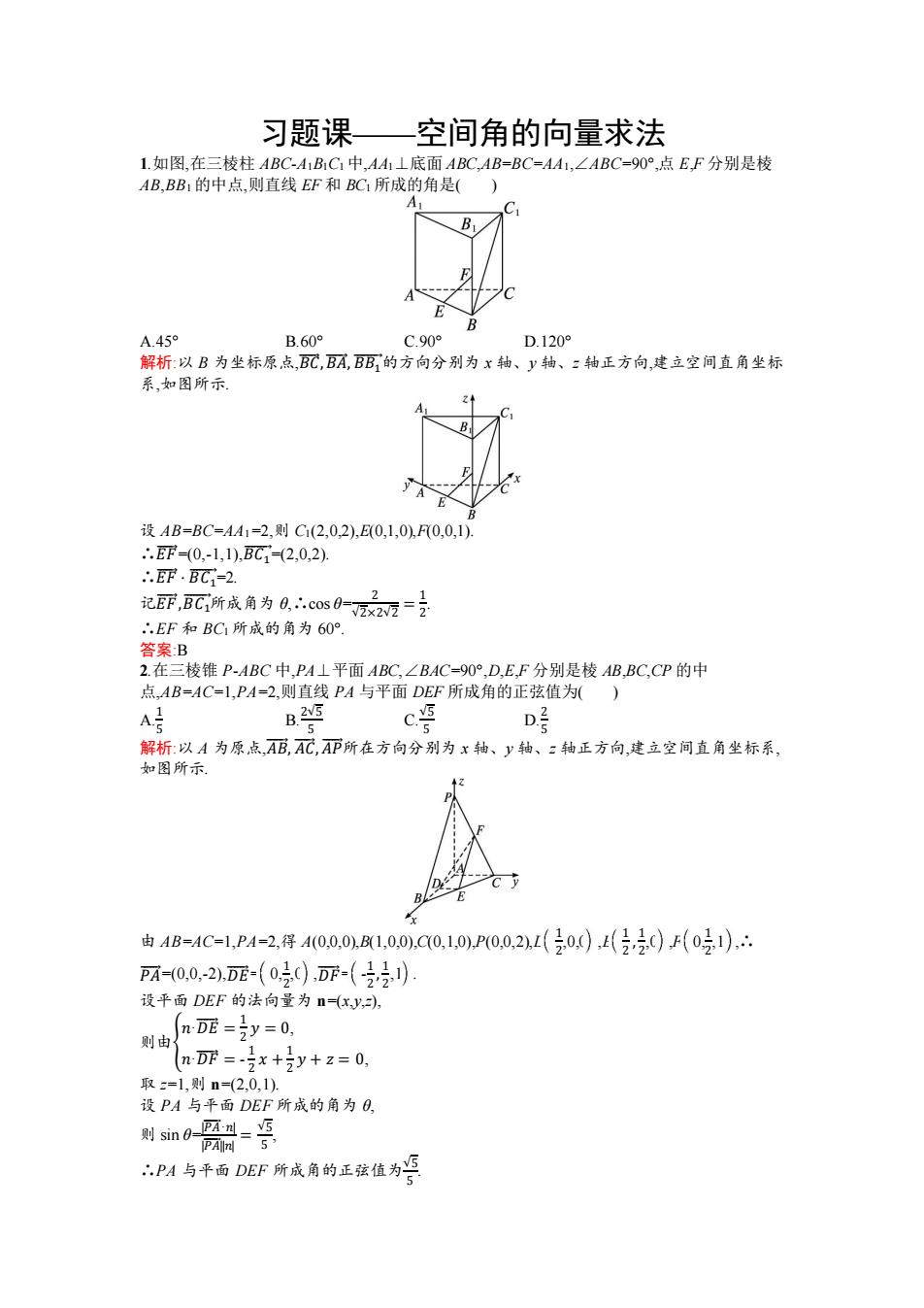
习题课— 空间角的向量求法 1.如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱 AB,BB1的中点,则直线EF和BC1所成的角是() A A.45° B.60° C.90° D.120° 解析:以B为坐标原点,配,BA,BB的方向分别为x轴、y轴、:轴正方向,建立空间直角坐标 系,如图所示 设AB=BC=AA1=2,则C(2,0,2),E(0,1,0),F0,0,1). ∴.EF=(0,-1,1),BC=(2,0,2) ∴.EF.BC=2. 记F,BC所成角为c0s0=z=克 ∴.EF和BC1所成的角为60°. 答案B 2.在三棱锥P-ABC中,PA⊥平面ABC,∠BAC-90°,D,E,F分别是棱AB,BC,CP的中 点,AB=AC-1,PA=2,则直线PA与平面DEF所成角的正弦值为() A时 B25 c D号 解析:以A为原点,AB,AC,AP所在方向分别为x轴、y轴、:轴正方向,建立空间直角坐标系, 如图所示」 由AB=AC=1,PA=2,得A(00,0,B1,00),C0,10),P00,2,L(20,),∠(22C),F(021) pm-00-2,呢-(20),丽-() 设平面DEF的法向量为n=(xy,), nD正-y=0, 则由 nD丽=-x+y+z=0, 取=1,则n=(2,0,1). 设PA与平面DEF所成的角为O, 则sin0-列=5 PAIn 5 ∴PA与平面DEF所成角的正弦值为
习题课——空间角的向量求法 1.如图,在三棱柱 ABC-A1B1C1 中,AA1⊥底面 ABC,AB=BC=AA1,∠ABC=90°,点 E,F 分别是棱 AB,BB1 的中点,则直线 EF 和 BC1 所成的角是( ) A.45° B.60° C.90° D.120° 解析:以 B 为坐标原点,𝐵𝐶⃗⃗⃗ ,𝐵𝐴⃗⃗⃗ , 𝐵𝐵1 ⃗⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标 系,如图所示. 设 AB=BC=AA1=2,则 C1(2,0,2),E(0,1,0),F(0,0,1). ∴𝐸𝐹⃗⃗ =(0,-1,1),𝐵𝐶1 ⃗⃗⃗⃗ =(2,0,2). ∴𝐸𝐹⃗⃗ · 𝐵𝐶1 ⃗⃗⃗⃗ =2. 记𝐸𝐹⃗⃗ ,𝐵𝐶1 ⃗⃗⃗⃗ 所成角为 θ,∴cos θ= 2 √2×2√2 = 1 2 . ∴EF 和 BC1 所成的角为 60°. 答案:B 2.在三棱锥 P-ABC 中,PA⊥平面 ABC,∠BAC=90°,D,E,F 分别是棱 AB,BC,CP 的中 点,AB=AC=1,PA=2,则直线 PA 与平面 DEF 所成角的正弦值为( ) A.1 5 B.2√5 5 C.√5 5 D.2 5 解析:以 A 为原点,𝐴𝐵⃗⃗⃗ , 𝐴𝐶⃗⃗ ,𝐴𝑃⃗⃗⃗ 所在方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标系, 如图所示. 由 AB=AC=1,PA=2,得 A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D 1 2 ,0,0 ,E 1 2 , 1 2 ,0 ,F 0,1 2 ,1 ,∴ 𝑃𝐴⃗⃗⃗ =(0,0,-2),𝐷𝐸⃗⃗⃗⃗ = 0,1 2 ,0 ,𝐷𝐹⃗⃗⃗ = - 1 2 , 1 2 ,1 . 设平面 DEF 的法向量为 n=(x,y,z), 则由{ 𝑛·𝐷𝐸⃗⃗⃗⃗ = 1 2 𝑦 = 0, 𝑛·𝐷𝐹⃗⃗⃗ = - 1 2 𝑥 + 1 2 𝑦 + 𝑧 = 0, 取 z=1,则 n=(2,0,1). 设 PA 与平面 DEF 所成的角为 θ, 则 sin θ= |𝑃𝐴⃗⃗⃗⃗⃗ ·𝑛| |𝑃𝐴⃗⃗⃗⃗⃗ ||𝑛| = √5 5 , ∴PA 与平面 DEF 所成角的正弦值为√5 5

答案C 3.己知四面体O-ABC的各棱长均为1,D是棱OA的中点,则异面直线BD与AC所成角的余 弦值为( A号 B时 D贤 解析:BD=0而-丽=0A-丽,AC=C-0A, ∴Dc=1,且D.元-0-死.0C-m)=月 ∴.cos 解得a=2-3或a=2+V3(舍去),所以AE-2-3. V(2-a)2+5 21 故选D 答案D 5图,等边三角形ABC与正方形ABDE有一公共边AB,二面角CABD的余弦值为号MW 分别是AC,BC的中点,则EM,AN所成角的余弦值为 C 解析:过点C作CO⊥平面ABDE,垂足为O,取AB的中点F,连接CF,OF,OA,OB则∠CFO为 二面角CAB-D的平面角
答案:C 3.已知四面体 O-ABC 的各棱长均为 1,D 是棱 OA 的中点,则异面直线 BD 与 AC 所成角的余 弦值为( ) A.√3 3 B.1 4 C.√3 6 D.√2 8 解析:∵𝐵𝐷⃗ ⃗ = 𝑂𝐷⃗⃗ − 𝑂𝐵⃗⃗⃗⃗ = 1 2 𝑂𝐴⃗⃗⃗ − 𝑂𝐵⃗⃗⃗⃗ ,𝐴𝐶⃗⃗ = ⃗𝑂𝐶⃗⃗ − 𝑂𝐴⃗⃗⃗ , ∴|𝐵𝐷⃗ ⃗ |=√3 2 ,|𝐴𝐶⃗⃗ |=1,且𝐵𝐷⃗ ⃗ · 𝐴𝐶⃗⃗ = 1 2 𝑂𝐴⃗⃗⃗ − 𝑂𝐵⃗⃗⃗⃗ ·(⃗𝑂𝐶⃗⃗ − 𝑂𝐴⃗⃗⃗ )=- 1 4 , ∴cos= ⃗𝐵𝐷⃗⃗⃗⃗⃗ ·𝐴𝐶⃗⃗⃗⃗ | ⃗𝐵𝐷⃗⃗⃗⃗⃗ ||𝐴𝐶⃗⃗⃗⃗ | = - 1 4 √3 2 ×1 =- √3 6 ,故异面直线 BD 与 AC 所成角的余弦值为√3 6 . 答案:C 4.如图,在四棱锥 P-ABCD 中,底面 ABCD 是矩形,PD⊥平面 ABCD,且 PD=AD=1,AB=2,点 E 是线段 AB 上一点,当二面角 P-EC-D 的大小为π 4时,AE=( ) A.1 B.1 2 C.2-√2 D.2-√3 解析:设 AE=a(0≤a≤2),以 D 为坐标原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝑃⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴的正方向, 建立空间直角坐标系 Dxyz,如图所示. 则 D(0,0,0),E(1,a,0),C(0,2,0),P(0,0,1),则𝑃𝐸⃗⃗⃗ =(1,a,-1),𝑃𝐶⃗⃗ =(0,2,-1). 设平面 PEC 的法向量为 m=(x,y,z), 则{ 𝑚·𝑃𝐸⃗⃗⃗ = 𝑥 + 𝑎𝑦-𝑧 = 0, 𝑚·𝑃𝐶⃗⃗ = 2𝑦-𝑧 = 0, 令 y=1,可得 x=2-a,z=2, 则 m=(2-a,1,2),易知平面 DEC 的一个法向量为𝐷𝑃⃗⃗⃗ =(0,0,1), 则|cos|=| 2 √(2-𝑎) 2+5 | = √2 2 ,解得 a=2-√3或 a=2+√3(舍去),所以 AE=2-√3. 故选 D. 答案:D 5.如图,等边三角形 ABC 与正方形 ABDE 有一公共边 AB,二面角 C-AB-D 的余弦值为√3 3 ,M,N 分别是 AC,BC 的中点,则 EM,AN 所成角的余弦值为 . 解析:过点 C 作 CO⊥平面 ABDE,垂足为 O,取 AB 的中点 F,连接 CF,OF,OA,OB,则∠CFO 为 二面角 C-AB-D 的平面角
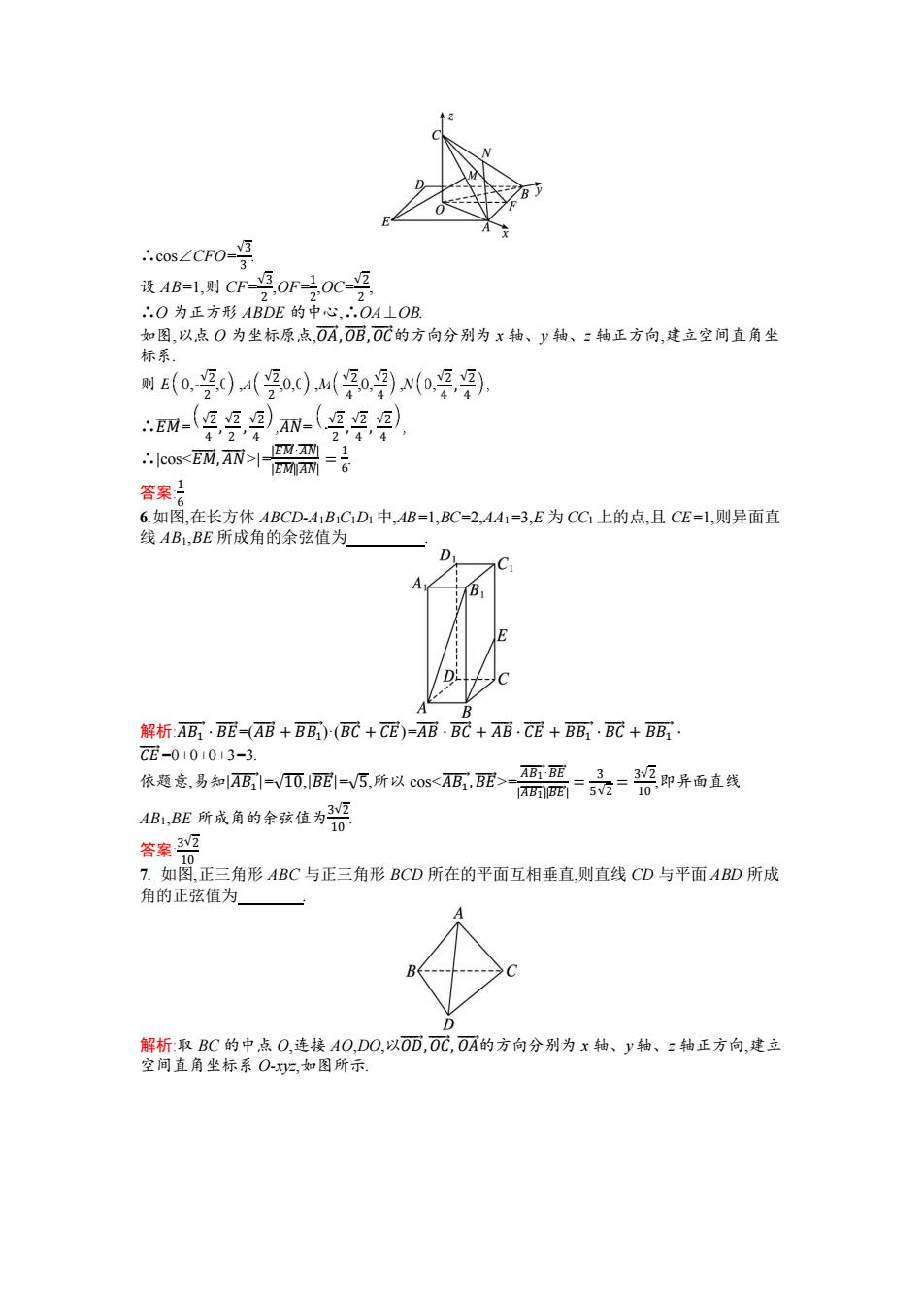
cos∠CFO- 3 设MB1,则CF是oF号oC-9 2 .O为正方形ABDE的中心,.OA⊥OB. 如图,以点O为坐标原点,0A,0丽0配的方向分别为x轴、y轴、z轴正方向,建立空间直角坐 标系 则(0,c)4(o,0)4(0,)No,,) ∴m-999丽-999 2’4’4 成丽圆器 答案 6.如图,在长方体ABCD-A1B1CD1中,AB=1,BC=2,AA1=3,E为CC上的点,且CE-1,则异面直 线AB1,BE所成角的余弦值为 B 解析:AB·BE=(AE+BB)(BC+CE)=AB.B配+AE.CE+BB,BC+BB. CE=0+0+0+3=3. 依题意,易知A-√而,配-5,所以c0s-正 源需-品普中异西直线 AB1,BE所成角的余弦值为 10 答案 10 7.如图,正三角形ABC与正三角形BCD所在的平面互相垂直,则直线CD与平面ABD所成 角的正弦值为 解析:取BC的中点O,连接AO,DO,以O而,OC,OA的方向分别为x轴、y轴、:轴正方向,建立 空间直角坐标系O-xz,如图所示
∴cos∠CFO=√3 3 . 设 AB=1,则 CF=√3 2 ,OF=1 2 ,OC=√2 2 , ∴O 为正方形 ABDE 的中心,∴OA⊥OB. 如图,以点 O 为坐标原点,𝑂𝐴⃗⃗⃗ ,𝑂𝐵⃗⃗⃗⃗ ,⃗𝑂𝐶⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐 标系. 则 E 0,- √2 2 ,0 ,A √2 2 ,0,0 ,M √2 4 ,0,√2 4 ,N 0,√2 4 , √2 4 , ∴𝐸𝑀⃗⃗⃗⃗ = √2 4 , √2 2 , √2 4 ,𝐴𝑁⃗ ⃗ = - √2 2 , √2 4 , √2 4 , ∴|cos|=|𝐸𝑀⃗⃗⃗⃗⃗⃗ · ⃗𝐴𝑁⃗⃗⃗⃗ | |𝐸𝑀⃗⃗⃗⃗⃗⃗ ||⃗𝐴𝑁⃗⃗⃗⃗ | = 1 6 . 答案: 1 6 6.如图,在长方体 ABCD-A1B1C1D1 中,AB=1,BC=2,AA1=3,E 为 CC1 上的点,且 CE=1,则异面直 线 AB1,BE 所成角的余弦值为 . 解析:𝐴𝐵1 ⃗⃗⃗⃗⃗ · 𝐵𝐸⃗⃗⃗ =(𝐴𝐵⃗⃗⃗ + 𝐵𝐵1 ⃗⃗⃗⃗⃗ )·(𝐵𝐶⃗⃗⃗ + 𝐶𝐸⃗⃗ )=𝐴𝐵⃗⃗⃗ · 𝐵𝐶⃗⃗⃗ + 𝐴𝐵⃗⃗⃗ · 𝐶𝐸⃗⃗ + 𝐵𝐵1 ⃗⃗⃗⃗⃗ · 𝐵𝐶⃗⃗⃗ + 𝐵𝐵1 ⃗⃗⃗⃗⃗ · 𝐶𝐸⃗⃗ =0+0+0+3=3. 依题意,易知|𝐴𝐵1 ⃗⃗⃗⃗⃗ |=√10,|𝐵𝐸⃗⃗⃗ |=√5,所以 cos= 𝐴𝐵1 ⃗⃗⃗⃗⃗⃗⃗⃗ ·𝐵𝐸⃗⃗⃗⃗⃗ |𝐴𝐵1 ⃗⃗⃗⃗⃗⃗⃗⃗ ||𝐵𝐸⃗⃗⃗⃗⃗ | = 3 5√2 = 3√2 10 ,即异面直线 AB1,BE 所成角的余弦值为3√2 10 . 答案: 3√2 10 7. 如图,正三角形 ABC 与正三角形 BCD 所在的平面互相垂直,则直线 CD 与平面 ABD 所成 角的正弦值为 . 解析:取 BC 的中点 O,连接 AO,DO,以𝑂𝐷⃗⃗ ,⃗𝑂𝐶⃗⃗ , 𝑂𝐴⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立 空间直角坐标系 O-xyz,如图所示

D 设BC=1,则A(0.0,月),(0,20),c(020),D(0,0),m=(,)BD=(号0)c而=( 皇) 设平面ABD的法向量为n=(xJy,), nm=y+号2=0, 则 n历-x+y=0, 取x=1,则y=-V3,z=1,所以n=(1,V3,1)为平面ABD的一个法向量. c0s_匹,因此直线CD与平面ABD所成角的正弦值为匹 5 答案雪 8.如图,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF-2V3,△ABC是以A为直角顶 点的等腰直角三角形,点P是线段BF上的一点,PF=3. (I)证明:FB⊥平面PAC: (2)求异面直线PC与AB所成的角的余弦值. (I)证明:如图,以A为原点,向量AB,AC,AF的方向分别为x轴、y轴、:轴的正方向建立空间 直角坐标系,则A(0,0,0),B(2,0,0),C(0,2,0),F0,0,23). .BF=VAB2 +AF2-4,PF=3, p号09m-2.0,2w)元-020-30 FE.AC0,∴FB⊥AC FE.AP=0,∴.FB⊥AP .FB⊥AC,FB⊥AP,ACAP=A, .FB⊥平面PAC (2解亚20.0,元(2月记亚与元的失角为8则cos需需=易=兴 9.如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=A41=3
设 BC=1,则 A 0,0,√3 2 ,B 0,- 1 2 ,0 ,C 0,1 2 ,0 ,D √3 2 ,0,0 ,𝐵𝐴⃗⃗⃗ = 0,1 2 , √3 2 ,𝐵𝐷⃗ ⃗ = √3 2 , 1 2 ,0 ,𝐶𝐷⃗⃗⃗ = √3 2 ,- 1 2 ,0 . 设平面 ABD 的法向量为 n=(x,y,z), 则{ 𝑛·𝐵𝐴⃗⃗⃗ = 1 2 𝑦 + √3 2 𝑧 = 0, 𝑛·𝐵𝐷⃗ ⃗ = √3 2 𝑥 + 1 2 𝑦 = 0, 取 x=1,则 y=-√3,z=1,所以 n=(1,-√3,1)为平面 ABD 的一个法向量. cos= √15 5 ,因此直线 CD 与平面 ABD 所成角的正弦值为√15 5 . 答案: √15 5 8.如图,在直二面角 E-AB-C 中,四边形 ABEF 是矩形,AB=2,AF=2√3,△ABC 是以 A 为直角顶 点的等腰直角三角形,点 P 是线段 BF 上的一点,PF=3. (1)证明:FB⊥平面 PAC; (2)求异面直线 PC 与 AB 所成的角的余弦值. (1)证明:如图,以 A 为原点,向量𝐴𝐵⃗⃗⃗ ,𝐴𝐶⃗⃗ ,𝐴𝐹⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴的正方向建立空间 直角坐标系,则 A(0,0,0),B(2,0,0),C(0,2,0),F(0,0,2√3). ∵BF=√𝐴𝐵2 + 𝐴𝐹2=4,PF=3, ∴P 3 2 ,0,√3 2 ,𝐹𝐵⃗⃗⃗ =(2,0,-2√3),𝐴𝐶⃗⃗ =(0,2,0),𝐴𝑃⃗⃗⃗ = 3 2 ,0,√3 2 . ∵𝐹𝐵⃗⃗⃗ · 𝐴𝐶⃗⃗ =0,∴FB⊥AC. ∵𝐹𝐵⃗⃗⃗ · 𝐴𝑃⃗⃗⃗ =0,∴FB⊥AP. ∵FB⊥AC,FB⊥AP,AC∩AP=A, ∴FB⊥平面 PAC. (2)解:∵𝐴𝐵⃗⃗⃗ =(2,0,0),𝑃𝐶⃗⃗ =(- 3 2 ,2,- √3 2 ),记𝐴𝐵⃗⃗⃗ 与𝑃𝐶⃗⃗ 的夹角为 θ,则|cos θ|=|𝐴𝐵⃗⃗⃗⃗⃗ ·𝑃𝐶⃗⃗⃗⃗ | |𝐴𝐵⃗⃗⃗⃗⃗ ||𝑃𝐶⃗⃗⃗⃗ | = |-3| 2√7 = 3√7 14 . 9.如图,在直棱柱 ABCD-A1B1C1D1 中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3

D B (I)证明:AC⊥B1D: (2)求直线B1C1与平面ACD1所成角的正弦值 (1)证明:易知AB,AD,AA1两两垂直. A D C B C 如图,以A为坐标原点,AB,AD,AA的方向分别为x轴、y轴、z轴正方向,建立空间直角坐标 系。 设AB=1,则A(0,0,0),B(1,0,0),B1(10,3),C1,1,0),C(亿,1,3),D(0,3,0),D1(0,3,3).从而B1D=(-1,3,- 3),AC=(1,1,0),BD=-(-1,3,0).因为4C⊥BD,所以AC·BD=-2+3+0=0.解得1=3或1=-V3(舍去) 于是B1D=(-V3,3,-3),AC-(3,1,0)因为AC.B1D=-3+3+0=0,所以AC⊥B1D,即AC⊥BD. (2)解:由(1)知,AD=-(0,3,3),AC=(3,1,0),B1C=(0,1,0) 设n=(是平面ACD,的一个法向量,则nC=V3x+y=0, (n:AD=3y+3z=0 令x=1,则n=(1,-V3,V3).设直线B1C1与平面ACD1所成角为0, 别m0eosn区C需-得-牙即直线B,G与平面4C0,所成角的正弦值为
(1)证明:AC⊥B1D; (2)求直线 B1C1 与平面 ACD1 所成角的正弦值. (1)证明:易知 AB,AD,AA1 两两垂直. 如图,以 A 为坐标原点,𝐴𝐵⃗⃗⃗ ,𝐴𝐷⃗⃗⃗⃗ ,𝐴𝐴1 ⃗⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标 系. 设 AB=t,则 A(0,0,0),B(t,0,0),B1(t,0,3),C(t,1,0),C1(t,1,3),D(0,3,0),D1(0,3,3).从而𝐵⃗⃗ 1 ⃗⃗⃗𝐷 =(-t,3,- 3),𝐴𝐶⃗⃗ =(t,1,0),𝐵𝐷⃗ ⃗ =(-t,3,0).因为 AC⊥BD,所以𝐴𝐶⃗⃗ · 𝐵𝐷⃗ ⃗ =-t 2+3+0=0.解得 t=√3或 t=-√3(舍去). 于是𝐵⃗⃗ 1 ⃗⃗⃗𝐷 =(-√3,3,-3),𝐴𝐶⃗⃗ =(√3,1,0).因为𝐴𝐶⃗⃗ · 𝐵⃗⃗ 1 ⃗⃗⃗𝐷 =-3+3+0=0,所以𝐴𝐶⃗⃗ ⊥ 𝐵⃗⃗ 1 ⃗⃗⃗𝐷 ,即 AC⊥B1D. (2)解:由(1)知,𝐴𝐷1 ⃗⃗⃗⃗⃗ =(0,3,3),𝐴𝐶⃗⃗ =(√3,1,0),𝐵1𝐶1 ⃗⃗⃗⃗⃗ =(0,1,0). 设 n=(x,y,z)是平面 ACD1 的一个法向量,则{ 𝑛·𝐴𝐶⃗⃗ = √3𝑥 + 𝑦 = 0, 𝑛·𝐴𝐷1 ⃗⃗⃗⃗⃗ = 3𝑦 + 3𝑧 = 0. 令 x=1,则 n=(1,-√3,√3).设直线 B1C1 与平面 ACD1 所成角为 θ, 则 sin θ=|cos|=| 𝑛·𝐵1𝐶1 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |𝑛||𝐵1𝐶1 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ | | = √3 √7 = √21 7 ,即直线 B1C1 与平面 ACD1 所成角的正弦值为 √21 7