1.2.4二面角 基础巩固 1.在一个二面角的两个面内,都和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二 面角的余弦值为() A.因 B..vis c D.以上都不对 6 6 解析:设这个二面角为0, 则cos0=0-13224 正 V中9xV+元= 6 则这个二面角的余弦值为匹或匹 6 6 答案:D 2.如图,在正方体ABCD-A1B1CD1中,E,F分别是BB1和DD1的中点,则平面ECF与平面 ABCD的夹角的余弦值为( A号 B c 答案B 3.已知在Rt△ABC中,∠C=90°,∠B=30°,AB=4,D为AB的中点,沿中线将△ACD折起使得 AB=V13,则二面角A-CD-B的大小为() A.60° B.90° C.120 D.150° 答案:C 4.在正方体ABCD-A1B1CD1中,点E为BB1的中点,则平面AED与平面ABCD所成的二面角 的余弦值为( A月 B明 c 吗 解析:以D为坐标原,点,DADC,DD1的方向分别为x轴、y轴、:轴正方向,建立空间直角坐标 系,如图所示 设正方体的棱长为1, 则D0,00)41(1,0,1),1(1,1 ∴DA=(1,0,1),D正=(1,1,》 设平面A1ED的一个法向量为n=(x,Jy,) 则所n=x+2=0 9{D正n=x+y+2z=0, 令x=1,则=1y-2》 n=(1,2-1) 又平面ABCD的一个法向量为DD1=(0,0,1)
1.2.4 二面角 基础巩固 1.在一个二面角的两个面内,都和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二 面角的余弦值为( ) A.√15 6 B.- √15 6 C.√15 3 D.以上都不对 解析:设这个二面角为 θ, 则 cos θ= (0,-1,3)·(2,2,4) √1+9×√4+4+16 = √15 6 , 则这个二面角的余弦值为√15 6 或- √15 6 . 答案:D 2.如图,在正方体 ABCD-A1B1C1D1 中,E,F 分别是 BB1 和 DD1 的中点,则平面 ECF 与平面 ABCD 的夹角的余弦值为( ) A.√3 3 B.√6 3 C.1 3 D.√2 3 答案:B 3.已知在 Rt△ABC 中,∠C=90°,∠B=30°,AB=4,D 为 AB 的中点,沿中线将△ACD 折起使得 AB=√13,则二面角 A-CD-B 的大小为( ) A.60° B.90° C.120° D.150° 答案:C 4.在正方体 ABCD-A1B1C1D1 中,点 E 为 BB1 的中点,则平面 A1ED 与平面 ABCD 所成的二面角 的余弦值为( ) A.- 1 2 B.2 3 C.√3 3 D.√2 2 解析:以 D 为坐标原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐标 系,如图所示. 设正方体的棱长为 1, 则 D(0,0,0),A1(1,0,1),E 1,1,1 2 . ∴𝐷𝐴1 ⃗⃗⃗⃗ =(1,0,1),𝐷𝐸⃗⃗⃗⃗ = 1,1,1 2 . 设平面 A1ED 的一个法向量为 n=(x,y,z). 则{ 𝐷𝐴1 ⃗⃗⃗⃗ ·𝑛 = 𝑥 + 𝑧 = 0, 𝐷𝐸⃗⃗⃗⃗ ·𝑛 = 𝑥 + 𝑦 + 1 2 𝑧 = 0, 令 x=1,则 z=-1,y=- 1 2 , ∴n= 1,- 1 2 ,-1 . 又平面 ABCD 的一个法向量为𝐷𝐷1 ⃗⃗⃗⃗ =(0,0,1)

1=2 又平面A1ED与平面ABCD所成的二面角为锐角, ∴平面AED与平面ABCD所成二面角的余弦值为号 答案B 5.已知四边形ABCD是正方形,E是AB的中点,将△DAE和△CBE分别沿DE,CE折起,使AE 与BE重合,A,B两点重合后记为点P,则二面角PCD-E的大小为() A.30° B.45° C.60° D.90° 解析:取CD的中点F,由二面角定义知∠PFE为其平面角,设PB=a,则EF=2a,in0品=克 ..二面角P-CD-E的大小为30° 答案:A 6.如图,二面角a-1-B的大小是60°,线段ABca,B∈1,AB与1所成的角为30°,则AB与平面B所 成的角的正弦值是」 B 解析:过点A作平面B的垂线,垂足为C,在平面B内过C作I的垂线,垂足为点D,连接AD B D 由三垂线定理可知ADL1,故∠ADC为二面角a-1B的平面角,大小为60 由已知,∠ABD=30°,连接CB,则∠ABC为AB与平面B所成的角. 设AD=2,则AC=V3,AB=AD sin306=4, 六sm4BC-希=年 答案 7.在边长为a的正三角形ABC中,ADLBC于D,沿AD折成二面角BAD-C后,BC0,这时= 面角B-AD-C的大小为 解析:∠BDC就是二面角B-AD-C的平面角. 又BC=BD=DC,国此△BDC为等边三角形,得∠BDC-号故二面角B-AD-C的大小为 答案 8.若正三棱锥的一个侧面的面积与底面积之比为2:3,则它的侧面和底面所成二面角的大小 为■ 答案:60° 9.在长方体ABCD-A1B1C1D1中,AB=4,BC=2,BB1=26,点E为AB的中点,过C1,D,E的平面 交BB1于点F D B B (1)求证:EF∥DC; (2)求二面角C-DE-C的大小 (I)证明:,平面ABB1A1∥平面DCC1D1,平面EFC DO平面AB=EF,平面EFC1Dn平面 DCCID1=DCI
∴cos= -1 √ 9 4 ×√1 =- 2 3 . 又平面 A1ED 与平面 ABCD 所成的二面角为锐角, ∴平面 A1ED 与平面 ABCD 所成二面角的余弦值为2 3 . 答案:B 5.已知四边形 ABCD 是正方形,E 是 AB 的中点,将△DAE 和△CBE 分别沿 DE,CE 折起,使 AE 与 BE 重合,A,B 两点重合后记为点 P,则二面角 P-CD-E 的大小为( ) A.30° B.45° C.60° D.90° 解析:取 CD 的中点 F,由二面角定义知∠PFE 为其平面角.设 PE=a,则 EF=2a,∴sin θ= 𝑎 2𝑎 = 1 2 , ∴二面角 P-CD-E 的大小为 30°. 答案:A 6.如图,二面角 α-l-β 的大小是 60°,线段 AB⊂α,B∈l,AB 与 l 所成的角为 30°,则 AB 与平面 β 所 成的角的正弦值是 . 解析:过点 A 作平面 β 的垂线,垂足为 C,在平面 β 内过 C 作 l 的垂线,垂足为点 D,连接 AD. 由三垂线定理可知 AD⊥l,故∠ADC 为二面角 α-l-β 的平面角,大小为 60°. 由已知,∠ABD=30°,连接 CB,则∠ABC 为 AB 与平面 β 所成的角. 设 AD=2,则 AC=√3,AB= 𝐴𝐷 sin30° =4, ∴sin∠ABC=𝐴𝐶 𝐴𝐵 = √3 4 . 答案: √3 4 7.在边长为 a 的正三角形 ABC 中,AD⊥BC 于 D,沿 AD 折成二面角 B-AD-C 后,BC=1 2 a,这时二 面角 B-AD-C 的大小为 . 解析:∠BDC 就是二面角 B-AD-C 的平面角. 又 BC=BD=DC=1 2 a,因此△BDC 为等边三角形,得∠BDC=π 3 ,故二面角 B-AD-C 的大小为π 3 . 答案: π 3 8.若正三棱锥的一个侧面的面积与底面积之比为 2∶3,则它的侧面和底面所成二面角的大小 为 . 答案:60° 9. 在长方体 ABCD-A1B1C1D1 中,AB=4,BC=2,BB1=2√6,点 E 为 AB 的中点,过 C1,D,E 的平面 交 BB1 于点 F. (1)求证:EF∥DC1; (2)求二面角 C1-DE-C 的大小. (1)证明:∵平面 ABB1A1∥平面 DCC1D1,平面 EFC1D∩平面 A1B=EF,平面 EFC1D∩平面 DCC1D1=DC1

.EF∥DC. (2)解:以D为坐标原点,DA,DC,DD的方向分别为x轴、y轴、:轴正方向,建立空间直角坐 标系,如图所示 则D(0,0,0),E(2,2,0,C1(0,4,2V6),C(0,4,0) 显然平面DEC的一个法向量为n=(0,0,1).设平面CDE的法向量m=(xy,), 则m死=2x+2y=0, (m-DC=4y+2V6z=0 4V6 令y=1,得x1,226=3 m-(1-1 1 /,c0s2延=元 又∈0,网∴号 故二面角C-DE-C的大小为鳄 拓展提高 1.在正四棱锥P-ABCD中,高为1,底边边长为2,则侧面与底面的夹角为() A.60° B.30° C.45° D.无法计算 解析:设O为底面ABCD的中心,E为BC的中点 .PE⊥BC,OE⊥BC, ∴∠PE0即为所求的二面角的平面角,tan∠PE0}l,∴∠PE0=45° 答案C 2.己知Rt△ABC的斜边AB在平面a内,直角顶点C在a内的射影是C,且C唯AB,则△ABC 是() A.直角三角形 B.钝角三角形 C.锐角三角形 D.各种情况都有可能 解析:易知AC<AC,BC<BC,而cOs∠4CB-AC2+BC2AB 2AC'BC .AC2+BC2=AB2,..AC2+BC2<AB2 ∴.cos∠ACB<0,即△ABC为钝角三角形 答案B 3.如图,在正四棱锥P-ABCD中,若△PAC的面积与正四棱锥的侧面面积之和的比为v√6:8,则 侧面与底面所成的二面角的大小为()
∴EF∥DC1. (2)解:以 D 为坐标原点,𝐷𝐴⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗ ,𝐷𝐷1 ⃗⃗⃗⃗ 的方向分别为 x 轴、y 轴、z 轴正方向,建立空间直角坐 标系,如图所示. 则 D(0,0,0),E(2,2,0),C1(0,4,2√6),C(0,4,0). 显然平面 DEC 的一个法向量为 n=(0,0,1).设平面 C1DE 的法向量 m=(x,y,z), 则{ 𝑚·𝐷𝐸⃗⃗⃗⃗ = 2𝑥 + 2𝑦 = 0, 𝑚·𝐷𝐶1 ⃗⃗⃗⃗⃗ = 4𝑦 + 2√6𝑧 = 0. 令 y=-1,得 x=1,z= 4 2√6 = √6 3 , ∴m= 1,-1,√6 3 ,cos= √6 3 2√6 3 = 1 2 . 又∈[0,π],∴= π 3 . 故二面角 C1-DE-C 的大小为π 3 . 拓展提高 1.在正四棱锥 P-ABCD 中,高为 1,底边边长为 2,则侧面与底面的夹角为( ) A.60° B.30° C.45° D.无法计算 解析:设 O 为底面 ABCD 的中心,E 为 BC 的中点, ∵PE⊥BC,OE⊥BC, ∴∠PEO 即为所求的二面角的平面角,tan∠PEO=1 1 =1,∴∠PEO=45°. 答案:C 2.已知 Rt△ABC 的斜边 AB 在平面 α 内,直角顶点 C 在 α 内的射影是 C',且 C'∉AB,则△ABC' 是( ) A.直角三角形 B.钝角三角形 C.锐角三角形 D.各种情况都有可能 解析:易知 AC'<AC,BC'<BC,而 cos∠AC'B=𝐴𝐶' 2+𝐵𝐶' 2 -𝐴𝐵 2 2𝐴𝐶'·𝐵𝐶' , ∵AC2+BC2=AB2 ,∴AC'2+BC'2<AB2 , ∴cos∠AC'B<0,即△ABC'为钝角三角形. 答案:B 3.如图,在正四棱锥 P-ABCD 中,若△PAC 的面积与正四棱锥的侧面面积之和的比为√6∶8,则 侧面与底面所成的二面角的大小为( )
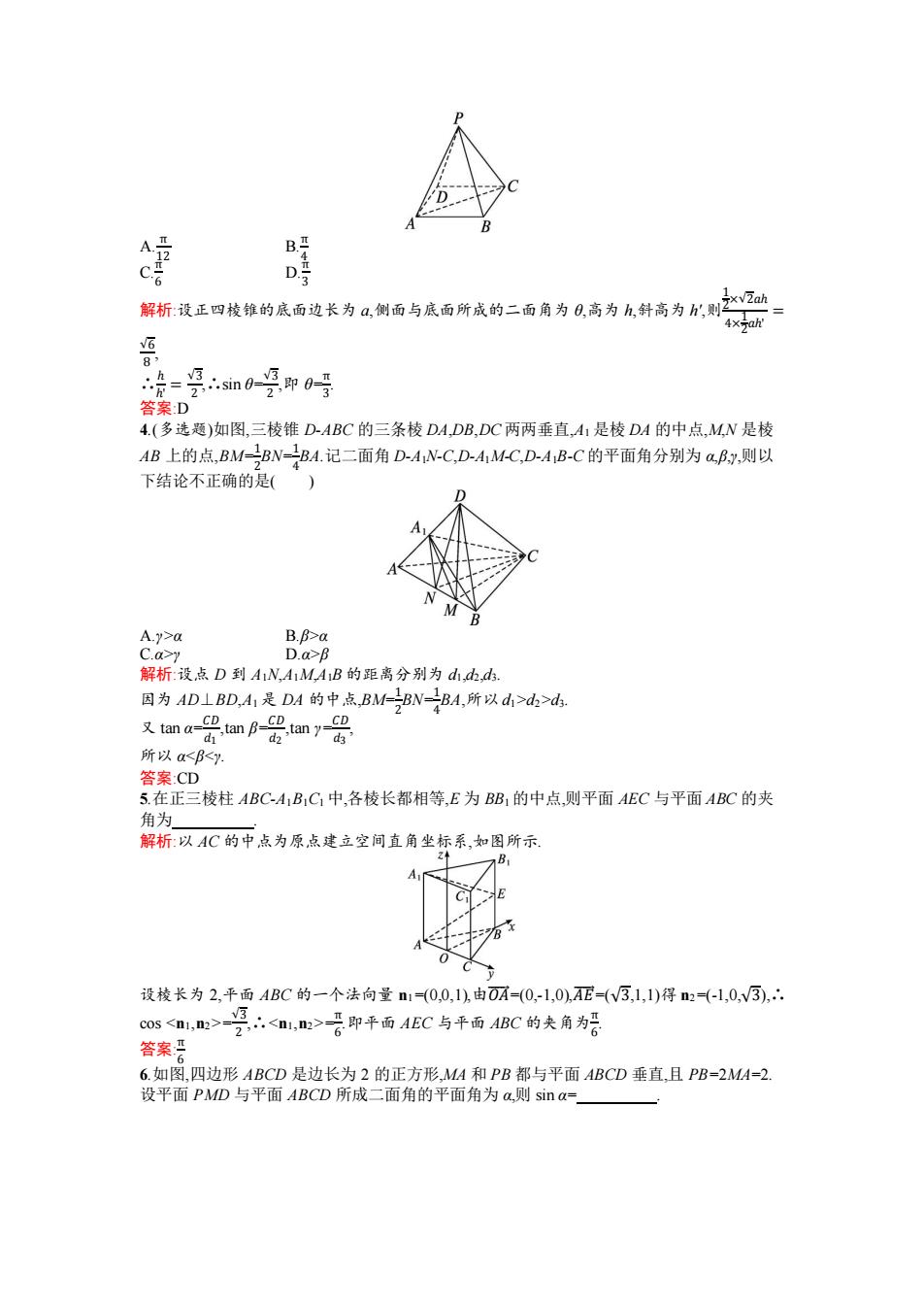
A号 c唔 解析:设正四技维的底面边长为侧面与底面所成的三面角为2高为么斜高为x而 4×2ah 6 8 治=只n0浮即0 2 答案D 4.(多选题)如图,三棱锥D-ABC的三条棱DA,DB,DC两两垂直,A1是棱DA的中点,M,N是棱 AB上的点,BM-BN-BA.记二面角D-4N-C,D-A1M-C,D-AB-C的平面角分别为aF,则以 下结论不正确的是() A A.y>a B.B>a C.a>y D.a-B 解析:设点D到AN,A1M,AB的距离分别为山,山,山. 国为AD LBD,A1是DA的中点,BMBN-BA,所以d>d山>d. 4 又ama器m月号m7号 所以a票即平面AEC与平面ABC的夫角为号 答案君 6.如图,四边形ABCD是边长为2的正方形,MA和PB都与平面ABCD垂直,且PB=2MA=2. 设平面PMD与平面ABCD所成二面角的平面角为a,则sina=
A. π 12 B.π 4 C.π 6 D.π 3 解析:设正四棱锥的底面边长为 a,侧面与底面所成的二面角为 θ,高为 h,斜高为 h',则 1 2 ×√2𝑎ℎ 4× 1 2 𝑎ℎ' = √6 8 , ∴ ℎ ℎ' = √3 2 ,∴sin θ= √3 2 ,即 θ= π 3 . 答案:D 4.(多选题)如图,三棱锥 D-ABC 的三条棱 DA,DB,DC 两两垂直,A1 是棱 DA 的中点,M,N 是棱 AB 上的点,BM=1 2 BN=1 4 BA.记二面角 D-A1N-C,D-A1M-C,D-A1B-C 的平面角分别为 α,β,γ,则以 下结论不正确的是( ) A.γ>α B.β>α C.α>γ D.α>β 解析:设点 D 到 A1N,A1M,A1B 的距离分别为 d1,d2,d3. 因为 AD⊥BD,A1 是 DA 的中点,BM=1 2 BN=1 4 BA,所以 d1>d2>d3. 又 tan α= 𝐶𝐷 𝑑1 ,tan β= 𝐶𝐷 𝑑2 ,tan γ= 𝐶𝐷 𝑑3 , 所以 α= √3 2 ,∴=π 6 .即平面 AEC 与平面 ABC 的夹角为π 6 . 答案: π 6 6.如图,四边形 ABCD 是边长为 2 的正方形,MA 和 PB 都与平面 ABCD 垂直,且 PB=2MA=2. 设平面 PMD 与平面 ABCD 所成二面角的平面角为 α,则 sin α=
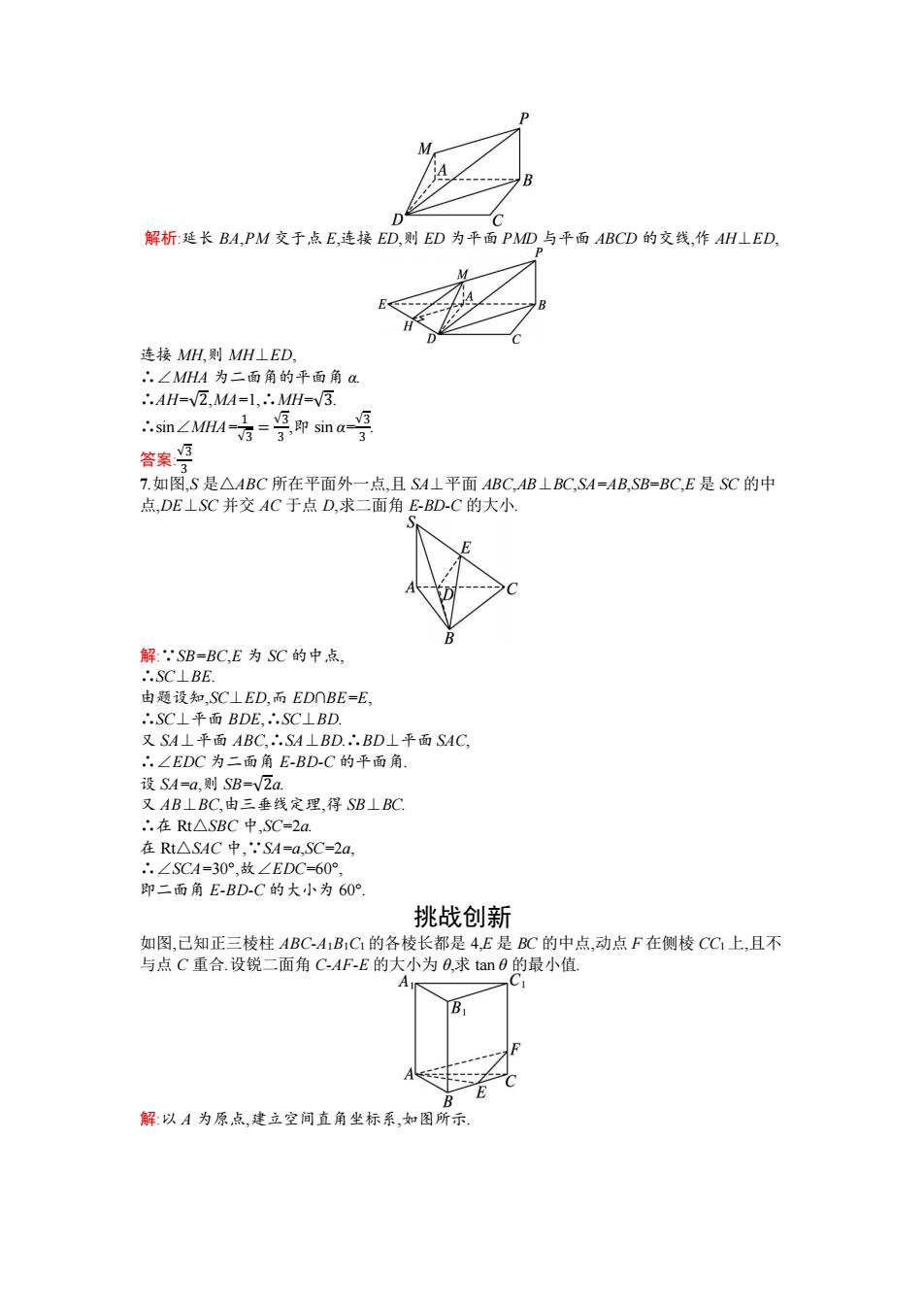
M B D 解析:延长BA,PM交于点E,连接ED,则ED为平面PMD与平面ABCD的交线,作AH⊥ED, M 连接MH,则MH⊥ED, ∴.∠MHA为二面角的平面角a ∴.AH=V2,MA=1,∴.MH=V3 m∠MA-7=9psna-9 3 答案 7.如图,S是△ABC所在平面外一点,且SA⊥平面ABC,AB⊥BC,SA=AB,SB=BC,E是SC的中 点,DE⊥SC并交AC于点D,求二面角EBD-C的大小. 解:SB=BC,E为SC的中点, ∴.SC⊥BE. 由题设知,SC⊥ED,而EDOBE=E, .SC⊥平面BDE,∴.SC⊥BD. 又SA⊥平面ABC,∴.SA⊥BD.∴.BD⊥平面SAC, ∴∠EDC为二面角E-BD-C的平面角. 设SA=a,则SB=√Za. 又AB⊥BC,由三垂线定理,得SB⊥BC ∴.在Rt△SBC中,SC=2a. 在Rt△SAC中,,SA=a,SC=2a ..∠SCA=30°故∠EDC=60° 即二面角E-BD-C的大小为60° 挑战创新 如图,己知正三棱柱ABC-A1B1C的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不 与点C重合.设锐二面角C-AF-E的大小为0,求tan0的最小值. 1 A长- B 解:以A为原点,建立空间直角坐标系,如图所示
解析:延长 BA,PM 交于点 E,连接 ED,则 ED 为平面 PMD 与平面 ABCD 的交线,作 AH⊥ED, 连接 MH,则 MH⊥ED, ∴∠MHA 为二面角的平面角 α. ∴AH=√2,MA=1,∴MH=√3. ∴sin∠MHA= 1 √3 = √3 3 ,即 sin α= √3 3 . 答案: √3 3 7.如图,S 是△ABC 所在平面外一点,且 SA⊥平面 ABC,AB⊥BC,SA=AB,SB=BC,E 是 SC 的中 点,DE⊥SC 并交 AC 于点 D,求二面角 E-BD-C 的大小. 解:∵SB=BC,E 为 SC 的中点, ∴SC⊥BE. 由题设知,SC⊥ED,而 ED∩BE=E, ∴SC⊥平面 BDE,∴SC⊥BD. 又 SA⊥平面 ABC,∴SA⊥BD.∴BD⊥平面 SAC, ∴∠EDC 为二面角 E-BD-C 的平面角. 设 SA=a,则 SB=√2a. 又 AB⊥BC,由三垂线定理,得 SB⊥BC. ∴在 Rt△SBC 中,SC=2a. 在 Rt△SAC 中,∵SA=a,SC=2a, ∴∠SCA=30°,故∠EDC=60°, 即二面角 E-BD-C 的大小为 60°. 挑战创新 如图,已知正三棱柱 ABC-A1B1C1 的各棱长都是 4,E 是 BC 的中点,动点 F 在侧棱 CC1 上,且不 与点 C 重合.设锐二面角 C-AF-E 的大小为 θ,求 tan θ 的最小值. 解:以 A 为原点,建立空间直角坐标系,如图所示

A B 设CF=(0<≤4),则由已知可得A(0,0,0),E(V3,3,0),F(0,4,,易得AE=(3,3,0),AF=(0,4). 设平面AEF的一个法向量为m=(xJy,), 由mL正,mL下可得m正=V3x+3y=0, m:AF=4y +z =0. 取m=(3无,-,4). 又由直三棱柱的性质可取平面AC℉的一个法向量为=(1,0,0),由0为锐角,可得cos 0-匹m=3 mln asin o-t 212+4 所以an0.2i6 1+16 V3A 由0<4,得≥京所以me目+=票故当4,即点F与点C重合时m0取得最小值
设 CF=λ(0<λ≤4),则由已知可得 A(0,0,0),E(√3,3,0),F(0,4,λ),易得𝐴𝐸⃗⃗⃗ =(√3,3,0),𝐴𝐹⃗⃗⃗ =(0,4,λ). 设平面 AEF 的一个法向量为 m=(x,y,z), 由 m⊥𝐴𝐸⃗⃗⃗ ,m⊥𝐴𝐹⃗⃗⃗ 可得{ 𝑚·𝐴𝐸⃗⃗⃗ = √3𝑥 + 3𝑦 = 0, 𝑚·𝐴𝐹⃗⃗⃗ = 4𝑦 + 𝜆𝑧 = 0. 取 m=(√3λ,-λ,4). 又由直三棱柱的性质可取平面 ACF 的一个法向量为 n=(1,0,0),由 θ 为锐角,可得 cos θ= |𝑚·𝑛| |𝑚||𝑛| = √3𝜆 2 √𝜆 2+4 ,sin θ= √𝜆 2+16 2 √𝜆 2+4 , 所以 tan θ= √𝜆 2+16 √3𝜆 = √ 1 3 + 16 3𝜆 2 . 由 0<λ≤4,得 1 𝜆 ≥ 1 4 ,所以 tan θ≥√ 1 3 + 1 3 = √6 3 ,故当 λ=4,即点 F 与点 C1 重合时,tan θ 取得最小值 √6 3