
第一章空间向量与立体几何 1.1空间向量及其运算 1.1.1空间向量及其运算 第1课时空间向量的概念与运算 1.如图,在四面体ABCD中,设G是CD的中点,则A正+(BD+C)等于() A.AD B.BG C.CD D.AG 解析A正+(B丽+B配)=正+B配-AC. 答案D 2.如图,四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点若 AB=a,AD=b,AA1=c,则C1M可以表示为( A.a+b+zc B.a-b+c C.-jab-c D.za+zb+c 解析:四棱柱ABCD-A1B1C1D1的底面是平行四边形,M是AC与BD的交点, ∴CM=C1C+CW=A1A-2E+AD)=-ca+b)=会-b-c 答案C 3.在四面体O-ABC中,OA=a,O丽=b,O元=c,D为BC的中点,E为AD的中点,则O尼=() A.za-zb+ic B.a-zb+zc Ca+ib+c D.ia+zb+ie 解析0正=O+A正=0i+AD=0丽+2×2(丽+AC)-0丽+(O-0i+0配- 0M0丽+0丽+0配=a+b+c 答案:C
第一章 空间向量与立体几何 1.1 空间向量及其运算 1.1.1 空间向量及其运算 第 1 课时 空间向量的概念与运算 1.如图,在四面体 ABCD 中,设 G 是 CD 的中点,则𝐴𝐵⃗⃗⃗ + 1 2 (𝐵𝐷⃗ ⃗ + 𝐵𝐶⃗⃗⃗ )等于( ) A.𝐴𝐷⃗⃗⃗⃗ B.𝐵𝐺⃗⃗⃗ C.𝐶𝐷⃗⃗⃗ D.𝐴𝐺⃗⃗⃗ 解析:𝐴𝐵⃗⃗⃗ + 1 2 (𝐵𝐷⃗ ⃗ + 𝐵𝐶⃗⃗⃗ )=𝐴𝐵⃗⃗⃗ + 𝐵𝐺⃗⃗⃗ = 𝐴𝐺⃗⃗⃗ . 答案:D 2.如图,四棱柱 ABCD-A1B1C1D1 的底面是平行四边形,M 是 AC 与 BD 的交点.若 𝐴𝐵⃗⃗⃗ =a,𝐴𝐷⃗⃗⃗⃗ =b,𝐴𝐴1 ⃗⃗⃗⃗⃗ =c,则𝐶⃗⃗ 1 ⃗⃗𝑀⃗ 可以表示为( ) A.a+b+ 1 2 c B.- 1 2 a- 1 2 b+c C.- 1 2 a- 1 2 b-c D.1 2 a+ 1 2 b+c 解析:∵四棱柱 ABCD-A1B1C1D1 的底面是平行四边形,M 是 AC 与 BD 的交点, ∴𝐶⃗⃗ 1 ⃗⃗𝑀⃗ = 𝐶⃗⃗ 1 ⃗𝐶 + 𝐶𝑀⃗⃗⃗ = 𝐴⃗⃗⃗ 1 ⃗𝐴⃗ − 1 2 (𝐴𝐵⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ )=-c- 1 2 (a+b)=- 1 2 a- 1 2 b-c. 答案:C 3.在四面体 O-ABC 中,𝑂𝐴⃗⃗⃗ =a,𝑂𝐵⃗⃗⃗⃗ =b,⃗𝑂𝐶⃗⃗ =c,D 为 BC 的中点,E 为 AD 的中点,则𝑂𝐸⃗⃗⃗ =( ) A.1 2 a- 1 4 b+ 1 4 c B.a- 1 2 b+ 1 2 c C.1 2 a+ 1 4 b+ 1 4 c D.1 4 a+ 1 2 b+ 1 4 c 解析:𝑂𝐸⃗⃗⃗ = 𝑂𝐴⃗⃗⃗ + 𝐴𝐸⃗⃗⃗ = 𝑂𝐴⃗⃗⃗ + 1 2 𝐴𝐷⃗⃗⃗⃗ = 𝑂𝐴⃗⃗⃗ + 1 2 × 1 2 (𝐴𝐵⃗⃗⃗ + 𝐴𝐶⃗⃗ )=𝑂𝐴⃗⃗⃗ + 1 4 (𝑂𝐵⃗⃗⃗⃗ − 𝑂𝐴⃗⃗⃗ + ⃗𝑂𝐶⃗⃗ − 𝑂𝐴⃗⃗⃗ )= 1 2 𝑂𝐴⃗⃗⃗ + 1 4 𝑂𝐵⃗⃗⃗⃗ + 1 4 ⃗𝑂𝐶⃗⃗ = 1 2 a+ 1 4 b+ 1 4 c. 答案:C

4.如图,在正方体ABCD-A1B1CD1中,点M,N分别是面对角线A1B与B1D1的中点.若 DA=a,D元-=b,DD=c,则MN=( ) A B A.(c+b-a) B.(a+b-c) C(a-e) D.c-a) 解析:MN=MA+A1D1+D1N, A B=AB-AA DC-DD =b-c, ∴MA-241-b-c .ADi--DA--a.D:N=DA+DC)-(a+b), ..MN--b-c)-a+i(a+b)--a+zc-7(c-a). 答案D 5.(多选题)下列命题是假命题的是() A方向相反的两个向量是相反向量 B.若向量a,b满足|a>bl,且a,b同向,则a>b C.不相等的两个空间向量的模必不相等 D.对于任何向量a,b,必有a+blsa+bl 解析:对于A:长度相等,且方向相反的两个向量是相反向量,故A是假命题:对于B:向量是不 能比较大小的,故B是假命题:对于C:不相等的两个空间向量的模也可以相等,故C是假命 题:D是真命题 答案:ABC 6.化简AB-AC+BC-BD-DA= 解析:AB-AC+BC-BD-DA=AE+BC+CA+AD+DB=AC+CA+AD+DE=AB. 答案AB 7.在正方体ABCD-A1B1CD1中,向量表达式AB-C而+BC-DA的化简结果为 解析:AB-C而+B配-DA-(AE+BC)-(C而+DA=AC-CA-2AC. 答案:2AC 8.如图,已知在四面体A-BCD中,AB=a-2c,CD=5a+6b-8c,对角线AC,BD的中点分别为E,F,则 EF- (用向量a,b,c表示) 解析:设G为BC的中点,连接EG,FG
4.如图,在正方体 ABCD-A1B1C1D1 中,点 M,N 分别是面对角线 A1B 与 B1D1 的中点.若 𝐷𝐴⃗⃗⃗⃗ =a,𝐷𝐶⃗⃗⃗ =b,𝐷𝐷1 ⃗⃗⃗⃗ =c,则𝑀𝑁⃗⃗⃗ =( ) A.1 2 (c+b-a) B.1 2 (a+b-c) C.1 2 (a-c) D.1 2 (c-a) 解析:∵𝑀𝑁⃗⃗⃗ = 𝑀𝐴1 ⃗⃗⃗ ⃗ + 𝐴1𝐷1 ⃗⃗⃗⃗ ⃗ + 𝐷⃗⃗ 1 ⃗𝑁⃗ , 𝐴⃗⃗⃗ 1 ⃗⃗𝐵 = 𝐴𝐵⃗⃗⃗ − 𝐴𝐴1 ⃗⃗⃗⃗⃗ = 𝐷𝐶⃗⃗⃗ − 𝐷𝐷1 ⃗⃗⃗⃗ =b-c, ∴𝑀𝐴1 ⃗⃗⃗ ⃗ =- 1 2 𝐴⃗⃗⃗ 1 ⃗⃗𝐵 =- 1 2 (b-c). ∵𝐴1𝐷1 ⃗⃗⃗⃗ ⃗ =-𝐷𝐴⃗⃗⃗⃗ =-a,𝐷⃗⃗ 1 ⃗𝑁⃗ = 1 2 (𝐷𝐴⃗⃗⃗⃗ + 𝐷𝐶⃗⃗⃗ )= 1 2 (a+b), ∴𝑀𝑁⃗⃗⃗ =- 1 2 (b-c)-a+ 1 2 (a+b)=- 1 2 a+ 1 2 c= 1 2 (c-a). 答案:D 5.(多选题)下列命题是假命题的是( ) A.方向相反的两个向量是相反向量 B.若向量 a,b 满足|a|>|b|,且 a,b 同向,则 a>b C.不相等的两个空间向量的模必不相等 D.对于任何向量 a,b,必有|a+b|≤|a|+|b| 解析:对于 A:长度相等,且方向相反的两个向量是相反向量,故 A 是假命题;对于 B:向量是不 能比较大小的,故 B 是假命题;对于 C:不相等的两个空间向量的模也可以相等,故 C 是假命 题;D 是真命题. 答案:ABC 6.化简𝐴𝐵⃗⃗⃗ − 𝐴𝐶⃗⃗ + 𝐵𝐶⃗⃗⃗ − 𝐵𝐷⃗ ⃗ − 𝐷𝐴⃗⃗⃗⃗ = . 解析:𝐴𝐵⃗⃗⃗ − 𝐴𝐶⃗⃗ + 𝐵𝐶⃗⃗⃗ − 𝐵𝐷⃗ ⃗ − 𝐷𝐴⃗⃗⃗⃗ = 𝐴𝐵⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ + 𝐶𝐴⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐵⃗ ⃗ = 𝐴𝐶⃗⃗ + 𝐶𝐴⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ + 𝐷𝐵⃗ ⃗ = 𝐴𝐵⃗⃗⃗ . 答案:𝐴𝐵⃗⃗⃗ 7.在正方体 ABCD-A1B1C1D1 中,向量表达式𝐴𝐵⃗⃗⃗ − 𝐶𝐷⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ − 𝐷𝐴⃗⃗⃗⃗ 的化简结果为 . 解析:𝐴𝐵⃗⃗⃗ − 𝐶𝐷⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ − 𝐷𝐴⃗⃗⃗⃗ =(𝐴𝐵⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ )-(𝐶𝐷⃗⃗⃗ + 𝐷𝐴⃗⃗⃗⃗ )=𝐴𝐶⃗⃗ − 𝐶𝐴⃗⃗ =2𝐴𝐶⃗⃗ . 答案:2𝐴𝐶⃗⃗ 8.如图,已知在四面体 A-BCD 中,𝐴𝐵⃗⃗⃗ =a-2c,𝐶𝐷⃗⃗⃗ =5a+6b-8c,对角线 AC,BD 的中点分别为 E,F,则 𝐸𝐹⃗⃗ = (用向量 a,b,c 表示). 解析:设 G 为 BC 的中点,连接 EG,FG
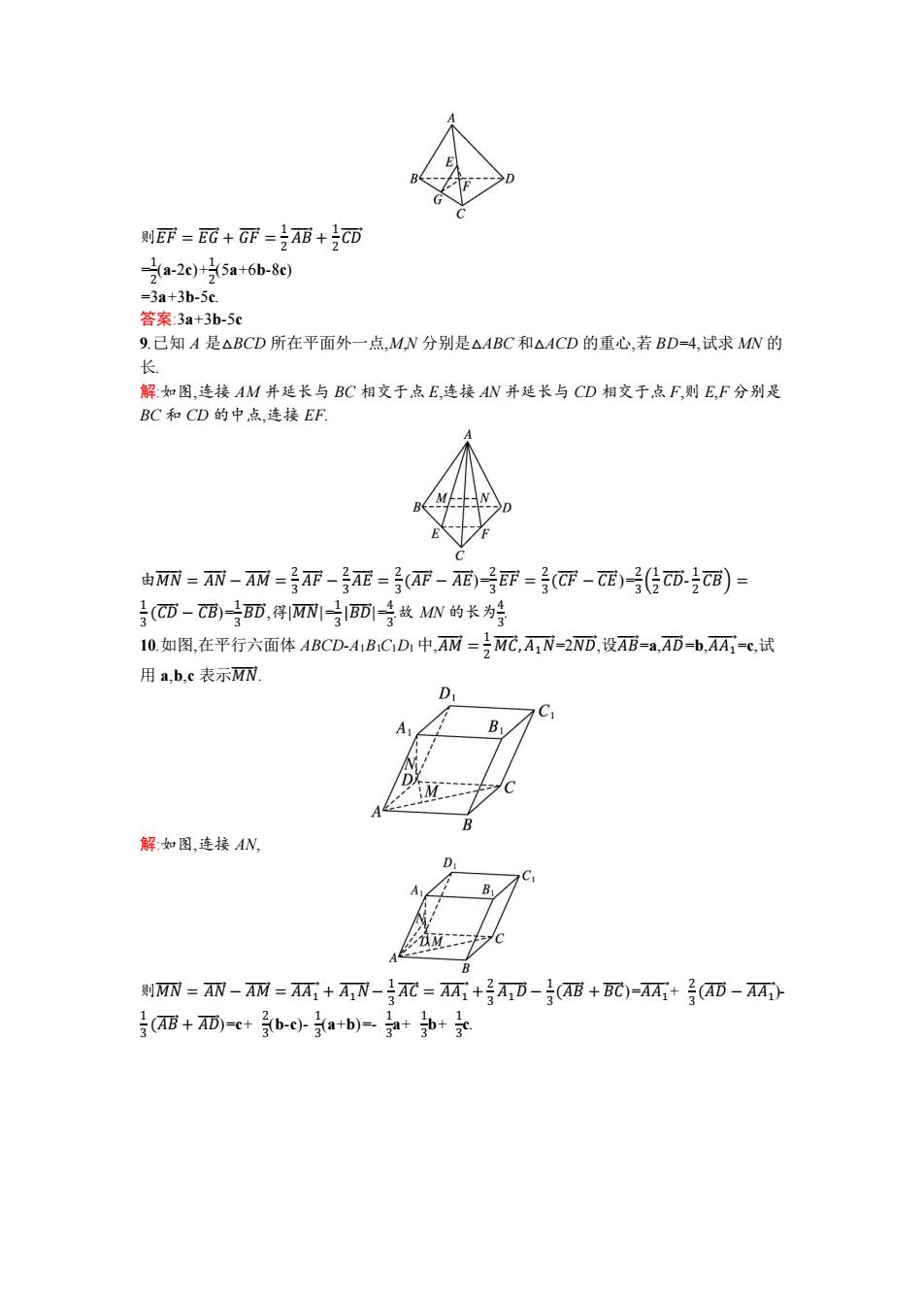
则乎-元+乎-丽+而 2a-2o)+25a+6b-8o) =3a+3b-5c 答案:3a+3b-5c 9.已知A是△BCD所在平面外一点,M,N分别是△ABC和△ACD的重心,若BD=4,试求MN的 长 解:如图,连接AM并延长与BC相交于点E,连接AN并延长与CD相交于点F,则E,F分别是 BC和CD的中点,连接EF 由M=AN-AM-子F-A正-子(征-A正)子F=CF-C)(而丽)= 而-®)D,得ND手故MN的长为等 10.如图,在平行六面体ABCD-A1B1CD1中,A-2MC,A1N-2ND,设A正=a,AD-b,AA=c,试 用a,b,c表示MN 解如图,连接AN, 则M=N-丽=不+A1N-C=瓜+号AD-丽+C)=环+子而- 3(a丽+D)=c+3b-c)-a+b)=+b+c
则𝐸𝐹⃗⃗ = 𝐸𝐺⃗⃗⃗ + 𝐺𝐹⃗⃗ = 1 2 𝐴𝐵⃗⃗⃗ + 1 2 𝐶𝐷⃗⃗⃗ = 1 2 (a-2c)+ 1 2 (5a+6b-8c) =3a+3b-5c. 答案:3a+3b-5c 9.已知 A 是△BCD 所在平面外一点,M,N 分别是△ABC 和△ACD 的重心,若 BD=4,试求 MN 的 长. 解:如图,连接 AM 并延长与 BC 相交于点 E,连接 AN 并延长与 CD 相交于点 F,则 E,F 分别是 BC 和 CD 的中点,连接 EF. 由𝑀𝑁⃗⃗⃗ = 𝐴𝑁⃗ ⃗ − 𝐴𝑀⃗⃗⃗⃗ = 2 3 𝐴𝐹⃗⃗⃗ − 2 3 𝐴𝐸⃗⃗⃗ = 2 3 (𝐴𝐹⃗⃗⃗ − 𝐴𝐸⃗⃗⃗ )= 2 3 𝐸𝐹⃗⃗ = 2 3 (𝐶𝐹⃗⃗ − 𝐶𝐸⃗⃗ )= 2 3 ( 1 2 𝐶𝐷⃗⃗⃗ - 1 2 𝐶𝐵⃗⃗⃗ ) = 1 3 (𝐶𝐷⃗⃗⃗ − 𝐶𝐵⃗⃗⃗ )= 1 3 𝐵𝐷⃗ ⃗ ,得|𝑀𝑁⃗⃗⃗ |=1 3 |𝐵𝐷⃗ ⃗ |=4 3 .故 MN 的长为4 3 . 10.如图,在平行六面体 ABCD-A1B1C1D1 中,𝐴𝑀⃗⃗⃗⃗ = 1 2 𝑀𝐶 ⃗⃗⃗ ,𝐴⃗⃗ 1 ⃗𝑁⃗ =2𝑁𝐷⃗⃗⃗ ,设𝐴𝐵⃗⃗⃗ =a,𝐴𝐷⃗⃗⃗⃗ =b,𝐴𝐴1 ⃗⃗⃗⃗⃗ =c,试 用 a,b,c 表示𝑀𝑁⃗⃗⃗ . 解:如图,连接 AN, 则𝑀𝑁⃗⃗⃗ = 𝐴𝑁⃗ ⃗ − 𝐴𝑀⃗⃗⃗⃗ = 𝐴𝐴1 ⃗⃗⃗⃗⃗ + 𝐴⃗⃗ 1 ⃗𝑁⃗ − 1 3 𝐴𝐶⃗⃗ = 𝐴𝐴1 ⃗⃗⃗⃗⃗ + 2 3 𝐴⃗⃗ 1 ⃗𝐷⃗ − 1 3 (𝐴𝐵⃗⃗⃗ + 𝐵𝐶⃗⃗⃗ )=𝐴𝐴1 ⃗⃗⃗⃗⃗ + 2 3 (𝐴𝐷⃗⃗⃗⃗ − 𝐴𝐴1 ⃗⃗⃗⃗⃗ )- 1 3 (𝐴𝐵⃗⃗⃗ + 𝐴𝐷⃗⃗⃗⃗ )=c+ 2 3 (b-c)- 1 3 (a+b)=- 1 3 a+ 1 3 b+ 1 3 c