
全程设计 第十一章立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱
第十一章立体几何初步 11.1 空间几何体 11.1.3 多面体与棱柱

课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解多面体的定义及其分类 2.理解棱柱的定义和结构特征, 3.掌握棱柱的分类 4.体会数学抽象的过程,加强直观想象、数学运算能力的培养
导航 课标定位素养阐释 1.了解多面体的定义及其分类. 2.理解棱柱的定义和结构特征. 3.掌握棱柱的分类. 4.体会数学抽象的过程,加强直观想象、数学运算能力的培养

导航 课前·基础认知 一、多面体 【问题思考】 1.在前面我们接触过长方体、正方体、棱柱、棱锥和棱台,它 们有什么共同点? 提示:它们都是由多个平面多边形围成的封闭几何体
导航 课前·基础认知 一、多面体 【问题思考】 1.在前面我们接触过长方体、正方体、棱柱、棱锥和棱台,它 们有什么共同点? 提示:它们都是由多个平面多边形围成的封闭几何体

导航 2.填空: ()构成多面体的基本元素 多面体是由若干个多边形所围成的封闭几何体. 多面体的面 围成多面体的各个 称为多面体的面 多面体的棱 两个面的公共边称为多面体的棱 多面体的 棱与棱的 称为多面体的顶点 顶点
导航 2.填空: (1)构成多面体的基本元素 多面体是由若干个平面多边形所围成的封闭几何体

导月 一个多面体中,连接同一面上两个顶点的线段, 多面体的 如果不是多面体的,就称其为多面体的面对 对角线 角线;连接 两个顶点的线段称为 多面体的体对角线 (2)凸多面体 把多面体的任意一个面延展为平面,如果其余的各面都在这 个平面的,那么称这样的多面体为凸多面体
导航 (2)凸多面体 把多面体的任意一个面延展为平面,如果其余的各面都在这 个平面的同一侧,那么称这样的多面体为凸多面体
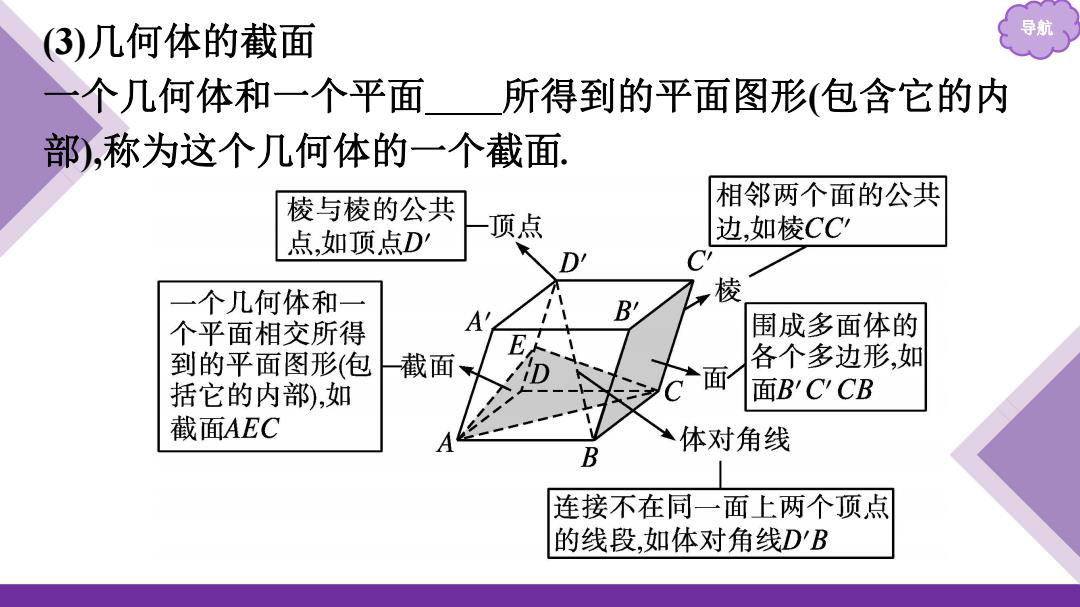
3)几何体的截面 导 一个几何体和一个平面 所得到的平面图形(包含它的内 部,称为这个几何体的一个截面 棱与棱的公共 相邻两个面的公共 点,如顶点D' 顶点 边,如棱CC 个几何体和一 棱 个平面相交所得 A 围成多面体的 到的平面图形(包 一截面 各个多边形,如 括它的内部),如 面 面BC'CB 截面AEC 体对角线 B 连接不在同一面上两个顶点 的线段,如体对角线D'B
导航 (3)几何体的截面 一个几何体和一个平面相交所得到的平面图形(包含它的内 部),称为这个几何体的一个截面

导航 (4)多面体的分类 多面体至少有4个面.多面体可以按照围成它的面的来命 名.可称为四面体、五面体、六面体等 (⑤)多面体的表面积 多面体 面的面积之和称为多面体的表面积(或全面积)
导航 (4)多面体的分类 多面体至少有4个面.多面体可以按照围成它的面的个数来命 名.可称为四面体、五面体、六面体等. (5)多面体的表面积 多面体所有面的面积之和称为多面体的表面积(或全面积)

导航 3.做一做:下列实物不能近似看成多面体的是( A.钻石 B.粉笔盒C篮球D.金字塔 解析:钻石、粉笔盒、金字塔都可以近似看成由若干个平面 多边形所围成的封闭几何体,所以它们都能近似看成多面体 篮球的表面不是平面多边形,故不能近似看成多面体, 答案:C
导航 3.做一做:下列实物不能近似看成多面体的是( ). A.钻石 B.粉笔盒 C.篮球 D.金字塔 解析:钻石、粉笔盒、金字塔都可以近似看成由若干个平面 多边形所围成的封闭几何体,所以它们都能近似看成多面体. 篮球的表面不是平面多边形,故不能近似看成多面体. 答案:C

导航 二、棱柱 【问题思考】 1棱柱中,至少有几组平面互相平行? 提示:一组
导航 二、棱柱 【问题思考】 1.棱柱中,至少有几组平面互相平行? 提示:一组