
全程设计 复习课 第1课时 解三角形
复习课 第1课时 解三角形

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破
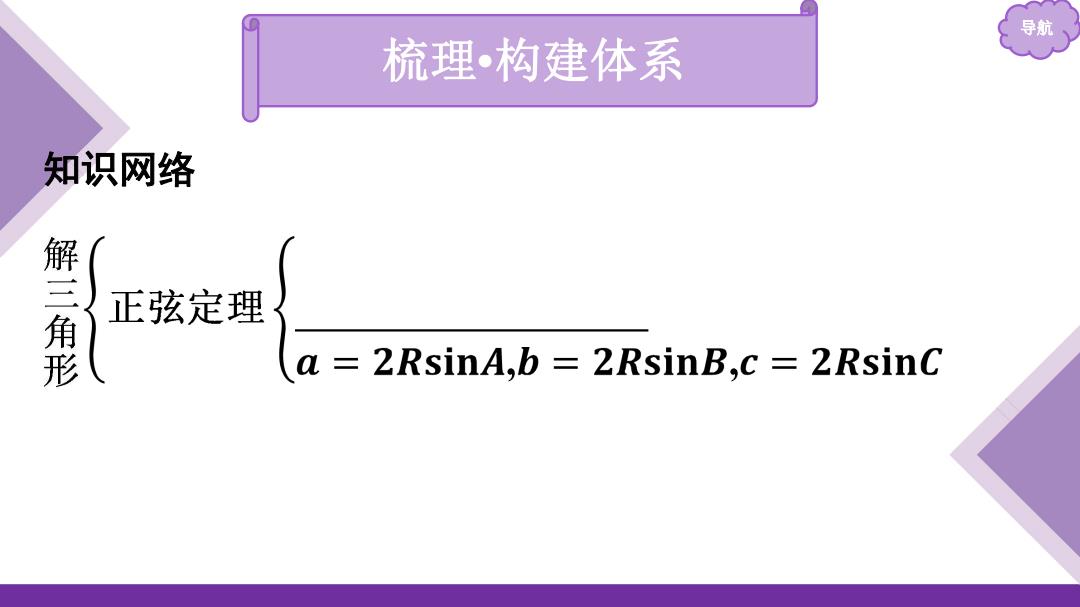
导航 梳理•构建体系 知识网络 三 正弦定理 形 a 2RsinA,b =2RsinB,c 2RsinC
导航 梳理•构建体系 知识网络
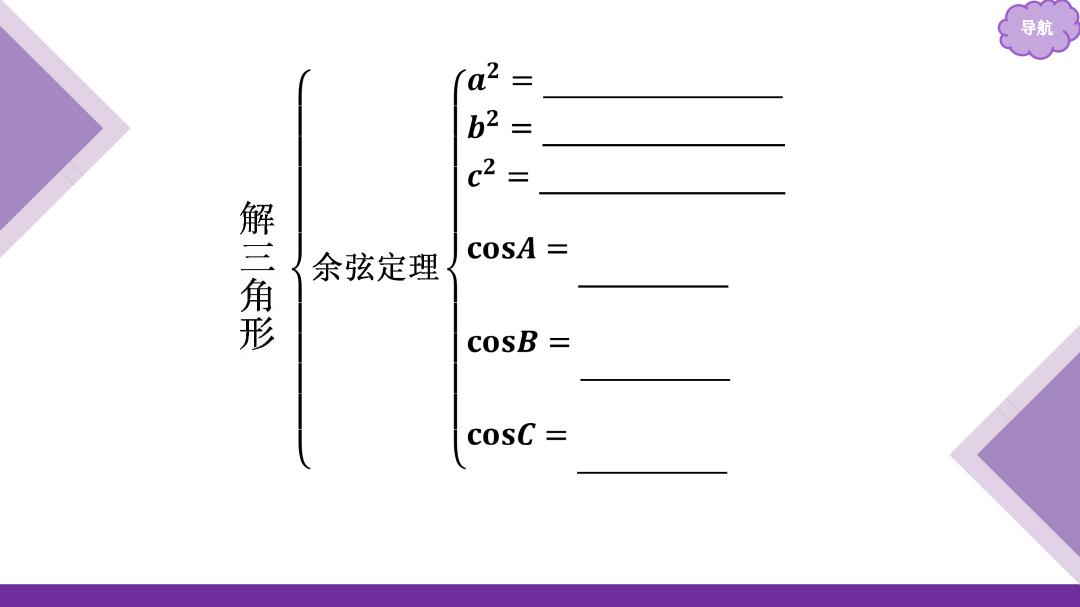
导航 b2 == 解三角形 cosA 三 余弦定理 cosB
导航

导航 距离 解三角形 正弦定理、余弦定理的应用{ 高度 角度 数学探究活动—得到不可达两点之间的距离
导航

导航 要点梳理 1.正弦定理的内容是什么? 提示:在△BC中, b sinB sinC' 2.余弦定理的内容是什么? 提示:在△ABC中,2=b2+c2-2bcc0sA,b2=a2+c2-2acc0sB,c2=2+b2- 2bc 2ac 2ab
导航 要点梳理 1.正弦定理的内容是什么? 2.余弦定理的内容是什么?

导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“V”,错误 的画“X” (1)正弦定理在钝角三角形中可能不成立(X) (2)若2+b2>c2,则△ABC为锐角三角形.(X) 3)解三角形时,只能用一次正弦或余弦定理(×) (4)在三角形中求角时,利用余弦定理不易产生增解(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√” ,错误 的画“×” . (1)正弦定理在钝角三角形中可能不成立.( ) (2)若a2+b2>c 2 ,则△ABC为锐角三角形.( ) (3)解三角形时,只能用一次正弦或余弦定理.( ) (4)在三角形中求角时,利用余弦定理不易产生增解.( ) × × × √

导航 归纳核心突破 专题整合 专题一应用正弦定理、 余弦定理解三角形 【例1】已知△ABC三个顶点的直角坐标分别为 A3,4),B(0,0),C(c,0). (1)若AB·AC=0,求c的值; (2)若c=5,求sinA的值, 分析:(1)根据向量数量积运算列方程求C;2)用正弦定理、余 弦定理求解
导航 归纳•核心突破 专题整合 专题一 应用正弦定理、余弦定理解三角形 【例1】 已知△ABC三个顶点的直角坐标分别为 A(3,4),B(0,0),C(c,0). (2)若c=5,求sin A的值. 分析:(1)根据向量数量积运算列方程求c;(2)用正弦定理、余 弦定理求解

导航 1)解法一:.A(3,4),B(0,0),C(C,0), AB=(-3,4),AC=(c-3,-4). 由AB.AC=0, 得(-3)×(c-3)+(-4)×(-4)=0. 解行行
导航

导航、 解法二:.'A(3,4),B(0,0),C(C,0), .,1AB12=32+42=25,AC2=(c-3)2+42,1BC2=c2 :AB.AC=0,∴.AB⊥AC .△ABC为直角三角形 由勾股定理,得AB+HAC=BC2. 即2-25+le-341,得c25
导航