
5.3.3 古典概型 基础巩固 1.下列随机试验的数学模型属于古典概型的是( A在一定的条件下,种一粒种子,它可能发芽,也可能不发芽 B.在平面直角坐标系内,从横坐标和纵坐标都为整数的所有点中任取一个点 C.某射手射击一次,可能命中0环、1环、2环、…、10环 D.四名同学用抽签的方法选一人去参加一个座谈会 答案D 2.四条线段的长度分别是1,3,5,7,从这四条线段中任取三条,则所取出的三条线段 能构成一个三角形的概率为() A号 B时 c D 解析:从四条长度各异的线段中任取一条,每条被取出的可能性均相等,所以该问 题属于古典概型.又所有样本点包括(1,3,5),(1,3,7),(1,5,7),(3,5,7),共4种,而能构成 三角形的样本点只有(3,5,7)一种,所以所取出的三条线段能构成一个三角形的概 率是P- 答案:A 3.在5张卡片上分别写上数字1,2,3,4,5,然后将它们混合后,再任意排成一行,则得 到的五位数能被2或5整除的概率是( ) A.0.2 B.0.4 C.0.6 D.0.8 解析:一个五位数能否被5整除关键看其个位数字,而由1,2,3,4,5组成的五位数 中,1,2,3,4,5出现在个位是等可能的.所以个位数字的样本空间2={1,2,3,4,5},“能 被2或5整除”这一事件中含有样本,点2,4,5所求概率为3=0.6.故选C 答案C 4.从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是 () A B.1 好 Di 解析:从1,2,3,4中任取2个不同的数有以下6种情 况(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满足取出的2个数之差的绝对值为2的有 (1,32,4),故所求概率是号= 答案B
5.3.3 古典概型 基础巩固 1.下列随机试验的数学模型属于古典概型的是( ) A.在一定的条件下,种一粒种子,它可能发芽,也可能不发芽 B.在平面直角坐标系内,从横坐标和纵坐标都为整数的所有点中任取一个点 C.某射手射击一次,可能命中 0 环、1 环、2 环、……、10 环 D.四名同学用抽签的方法选一人去参加一个座谈会 答案:D 2.四条线段的长度分别是 1,3,5,7,从这四条线段中任取三条,则所取出的三条线段 能构成一个三角形的概率为( ) A. 1 4 B. 1 3 C. 1 2 D. 2 5 解析:从四条长度各异的线段中任取一条,每条被取出的可能性均相等,所以该问 题属于古典概型.又所有样本点包括(1,3,5),(1,3,7),(1,5,7),(3,5,7),共 4 种,而能构成 三角形的样本点只有(3,5,7)一种,所以所取出的三条线段能构成一个三角形的概 率是 P=1 4 . 答案:A 3.在 5 张卡片上分别写上数字 1,2,3,4,5,然后将它们混合后,再任意排成一行,则得 到的五位数能被 2 或 5 整除的概率是( ) A.0.2 B.0.4 C.0.6 D.0.8 解析:一个五位数能否被 5 整除关键看其个位数字,而由 1,2,3,4,5 组成的五位数 中,1,2,3,4,5 出现在个位是等可能的.所以个位数字的样本空间 Ω={1,2,3,4,5},“能 被 2 或 5 整除”这一事件中含有样本点 2,4,5,所求概率为3 5 =0.6.故选 C. 答案:C 4.从 1,2,3,4 中任取 2 个不同的数,则取出的 2 个数之差的绝对值为 2 的概率是 ( ) A. 1 2 B. 1 3 C. 1 4 D. 1 6 解析:从 1,2,3,4 中任取 2 个不同的数有以下 6 种情 况:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满足取出的 2 个数之差的绝对值为 2 的有 (1,3),(2,4),故所求概率是2 6 = 1 3 . 答案:B

5.在第1,3,4,5,8路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车), 有一名乘客等候第4路或第8路汽车.假定当时各路汽车首先到站的可能性相等 则首先到站正好是这名乘客所需乘的汽车的概率等于( ) A号 B . 解析:由题知,在该问题中,基本事件总数为5,“一名乘客等车”这一事件包含2个 基本事件,故所求概率为P号 答案D 6.从集合{a,b,c,d,e}的所有子集中任取一个,这个集合恰好是集合{a,b,c}的子集的 概率是( A.1 B时 c 解析:集合{a,b,c,d,e}的所有子集有2=32个,集合{a,b,c}的所有子集有23=8个,故 所求概率为是= 答案:C 7.掷一个均匀的骰子,骰子落地时朝上的面的点数是3的倍数的概率是 解析:梯骰子的结果共有6种,其中是3的倍数的结果有2种,故所求概率为后= 答案 8.从1,2,3,4,5,6这六个数中,不放回地任取两个数,两个数都是偶数的概率是 解析:样本点共有15个,它们是 (1,2),1,3),1,4),1,5),(1,6),(2,3),(2,4).(2,5),(2,6),3,4),(3,5),(3,6).(4,5),(4,6),(5,6),其中 两个数都是偶数的有2,4),2,6.4,6,共3个,故P=品=目 答案 9.四张卡片上分别写有数字1,2,3,4,从这四张卡片中随机抽取2张,则取出的2张 卡片上的数字之和为奇数的概率为 解析:由题意知,样本空间2={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},记“取出的2张卡 片上的数字之和为奇数”为事件A,则A={1,21,4.2,3)(6,4},故P4A)-g= 答案号 10.依据闯关游戏规则,请你探究图中闯关游戏的奥秘:要求每次同时按下左边和 右边各1个按钮(按钮分别标记为左1,左2,右1,右2),其中按下某些按钮可以使 灯泡点亮若点亮灯泡则闯关成功:否则,闯关失败 99 98 ()用列表的方法表示所有可能的按按钮方式
5.在第 1,3,4,5,8 路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车), 有一名乘客等候第 4 路或第 8 路汽车.假定当时各路汽车首先到站的可能性相等, 则首先到站正好是这名乘客所需乘的汽车的概率等于( ) A. 1 2 B. 2 3 C. 3 5 D. 2 5 解析:由题知,在该问题中,基本事件总数为 5,“一名乘客等车”这一事件包含 2 个 基本事件,故所求概率为 P=2 5 . 答案:D 6.从集合{a,b,c,d,e}的所有子集中任取一个,这个集合恰好是集合{a,b,c}的子集的 概率是( ) A.1 B. 1 2 C. 1 4 D. 1 8 解析:集合{a,b,c,d,e}的所有子集有 2 5=32 个,集合{a,b,c}的所有子集有 2 3=8 个,故 所求概率为 8 32 = 1 4 . 答案:C 7.掷一个均匀的骰子,骰子落地时朝上的面的点数是 3 的倍数的概率是 . 解析:掷骰子的结果共有 6 种,其中是 3 的倍数的结果有 2 种,故所求概率为2 6 = 1 3 . 答案: 1 3 8.从 1,2,3,4,5,6 这六个数中,不放回地任取两个数,两个数都是偶数的概率是 . 解析:样本点共有 15 个,它们是 (1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),其中 两个数都是偶数的有(2,4),(2,6),(4,6),共 3 个,故 P= 3 15 = 1 5 . 答案: 1 5 9.四张卡片上分别写有数字 1,2,3,4,从这四张卡片中随机抽取 2 张,则取出的 2 张 卡片上的数字之和为奇数的概率为 . 解析:由题意知,样本空间 Ω={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},记“取出的 2 张卡 片上的数字之和为奇数”为事件 A,则 A={(1,2),(1,4),(2,3),(3,4)},故 P(A)= 4 6 = 2 3 . 答案: 2 3 10.依据闯关游戏规则,请你探究图中闯关游戏的奥秘:要求每次同时按下左边和 右边各 1 个按钮(按钮分别标记为左 1,左 2,右 1,右 2),其中按下某些按钮可以使 灯泡点亮.若点亮灯泡,则闯关成功;否则,闯关失败. (1)用列表的方法表示所有可能的按按钮方式;

(2)若只有两个1号按钮同时按下才能点亮灯泡,试求闯关成功的概率 解(1)所有可能的按钮方式列表如下: 右1 右2 左1 (左1,右1) (左1,右2) 左2 (左2,右1) (左2,右2) 2)若只有两个1号按钮同时按下才能点亮灯泡,则P(间关成功)子 11.某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同 小球的抽奖箱中,每次取出一个球,记下编号后放回,连续取两次.若取出的两个小 球编号相加之和等于6则中一等奖:若等于5,则中二等奖:若等于4或3,则中三等 奖 (1)求中三等奖的概率: (2)求中奖的概率 解:设“中三等奖”为事件A,“中奖”为事件B,从四个小球中有放回地取两个,有 (0,0).(0,1).(0,2),0,3),(1,0),(1,1),(1,2).(1,3),(2,0),(2,1),(2,2),2,3).3,0),(3,1),(3,2),(3,3) ,共16种不同的结果 (1)取出的两个小球编号相加之和等于4或3的取法有 (1,3),2,23,1),0,3),1,22,1,3,0),共7种结果,则中三等奖的概率为P4品 (2)由(1)知两个小球编号相加之和等于3或4的取法有7种:两个小球编号相加之 和等于5的取法有2种(2,3),(3,2)两个小球编号相加之和等于6的取法有1 种(3,3) 故中奖的概率为P心®)=昌 16 12.(1)从含有两件正品a,b和一件次品c的3件产品中每次任取一件,取出后不放 回,连续取两次,求取出的两件产品中恰有一件次品的概率, (2)将(1)中条件“取出后不放回”改为每次取出后放回”其余不变,再求取出的两件 产品中恰有一件次品的概率 解(I)样本空间2={(a,b),(a,c,b,c),b,a),(c,a,(c,b)},其中(a,b)中的a表示第一次 取出的产品,b表示第二次取出的产品,2中有6个基本事件,它们的出现都是等 可能的,事件A=“取出的两件产品中,恰好有一件次品”包含4个基本事件,则 PMF名= (2)有放回地连续取两件,样本空间 2={(a,a),(a,b),(a,c,b,b),b,a),b,c,(c,c),(c,a),(c,b)}中共9个等可能的基本事件,事 件B=“恰有一件次品”包含4个基本事件,则PB)=。 拓展提高 1.欲寄出两封信,现有两个邮箱供选择,则两封信都投到同一个邮箱的概率是 ()
(2)若只有两个 1 号按钮同时按下才能点亮灯泡,试求闯关成功的概率. 解:(1)所有可能的按钮方式列表如下: 右 1 右 2 左 1 (左 1,右 1) (左 1,右 2) 左 2 (左 2,右 1) (左 2,右 2) (2)若只有两个 1 号按钮同时按下才能点亮灯泡,则 P(闯关成功)= 1 4 . 11.某商场举行购物抽奖促销活动,规定每位顾客从装有编号为 0,1,2,3 四个相同 小球的抽奖箱中,每次取出一个球,记下编号后放回,连续取两次.若取出的两个小 球编号相加之和等于 6,则中一等奖;若等于 5,则中二等奖;若等于 4 或 3,则中三等 奖. (1)求中三等奖的概率; (2)求中奖的概率. 解:设“中三等奖”为事件 A,“中奖”为事件 B,从四个小球中有放回地取两个,有 (0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3) ,共 16 种不同的结果. (1)取出的两个小球编号相加之和等于 4 或 3 的取法有 (1,3),(2,2),(3,1),(0,3),(1,2),(2,1),(3,0),共 7 种结果,则中三等奖的概率为 P(A)= 7 16 . (2)由(1)知两个小球编号相加之和等于 3 或 4 的取法有 7 种;两个小球编号相加之 和等于 5 的取法有 2 种:(2,3),(3,2);两个小球编号相加之和等于 6 的取法有 1 种:(3,3). 故中奖的概率为 P(B)= 7+2+1 16 = 5 8 . 12.(1)从含有两件正品 a,b 和一件次品 c 的 3 件产品中每次任取一件,取出后不放 回,连续取两次,求取出的两件产品中恰有一件次品的概率; (2)将(1)中条件“取出后不放回”改为“每次取出后放回”其余不变,再求取出的两件 产品中恰有一件次品的概率. 解:(1)样本空间 Ω={(a,b),(a,c),(b,c),(b,a),(c,a),(c,b)},其中(a,b)中的 a 表示第一次 取出的产品,b 表示第二次取出的产品,Ω 中有 6 个基本事件,它们的出现都是等 可能的,事件 A=“取出的两件产品中,恰好有一件次品”包含 4 个基本事件,则 P(A)= 4 6 = 2 3 . (2)有放回地连续取两件,样本空间 Ω={(a,a),(a,b),(a,c),(b,b),(b,a),(b,c),(c,c),(c,a),(c,b)}中共 9 个等可能的基本事件,事 件 B=“恰有一件次品”包含 4 个基本事件,则 P(B)= 4 9 . 拓展提高 1.欲寄出两封信,现有两个邮箱供选择,则两封信都投到同一个邮箱的概率是 ( )

号 时 c D 解析:可记两封信为1,2,两个邮箱为甲、乙,则寄出两封信,有两个邮箱供选择,有 以下几种结果 1放在甲中,而2放在乙中2放在甲中,而1放在乙中;1,2均放在甲中;1,2均放在 乙中 由上可知,两封信都投到同一个邮箱的结果数为2 所以,两封信都授到同一个邮箱的概率为 答案:A 2.从所有3位正整数中任取一个数,则此数以2为底的对数也是正整数的概率为 () A宏 B.1 c D.以上全不对 '300 解析:三位的正整数共有900个,若以2为底的对数也是正整数(设为),则 100≤2≤99,解得n=7,89,共3个故P=品=00 答案B 3.有一对年轻夫妇给他们12个月大的婴儿拼排3块分别写有20“12”和中国” 的字块.如果婴儿能够排成2012中国”或者“中国2012”,那么他们就给婴 儿奖励.假设婴儿能将字块挨着正排,则这个婴儿能得到奖励的概率是() A B时 ci D 解析:3块字块的排法为2012中国”,20中国12”,“1220中国”,“12 中国20”,“中国2012”,“中国1220”,共6种,婴儿能得到奖励的情况有2 种,故所求概率P2= 答案B 4将一个各个面上涂有颜色的正方体锯成27个同样大小的小正方体,从这些小正 方体中任取1个,则恰有两面涂有颜色的概率是() A B房 c p 解析:共有27个小正方体,每条棱的中间位置上有一个是两个面涂有颜色的小正 方体,共有12个,所以P号=号 答案D 5.若以连续掷两次均匀的骰子分别得到的点数m,n作为点P的坐标,则点P满足 x2+y2≤16的概率是 解析:连续掷两次均匀的骰子,得到点数m,n记作P(m,n),共有36种情况,其中点 P(m,n)满足x2+y2≤16的有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),共8种情况 所以P品=子 36
A. 1 2 B. 1 4 C. 3 4 D. 3 8 解析:可记两封信为 1,2,两个邮箱为甲、乙,则寄出两封信,有两个邮箱供选择,有 以下几种结果: 1 放在甲中,而 2 放在乙中;2 放在甲中,而 1 放在乙中;1,2 均放在甲中;1,2 均放在 乙中. 由上可知,两封信都投到同一个邮箱的结果数为 2. 所以,两封信都投到同一个邮箱的概率为1 2 . 答案:A 2.从所有 3 位正整数中任取一个数,则此数以 2 为底的对数也是正整数的概率为 ( ) A. 1 225 B. 1 300 C. 1 450 D.以上全不对 解析:三位的正整数共有 900 个,若以 2 为底的对数也是正整数(设为 n),则 100≤2 n≤999,解得 n=7,8,9,共 3 个,故 P= 3 900 = 1 300 . 答案:B 3.有一对年轻夫妇给他们 12 个月大的婴儿拼排 3 块分别写有“20”“12”和“中国” 的字块.如果婴儿能够排成“20 12 中国”或者“中国 20 12”,那么他们就给婴 儿奖励.假设婴儿能将字块挨着正排,则这个婴儿能得到奖励的概率是( ) A. 1 2 B. 1 3 C. 1 4 D. 1 6 解析:3 块字块的排法为“20 12 中国”,“20 中国 12”,“12 20 中国”,“12 中国 20”,“中国 20 12”,“中国 12 20”,共 6 种,婴儿能得到奖励的情况有 2 种,故所求概率 P=2 6 = 1 3 . 答案:B 4.将一个各个面上涂有颜色的正方体锯成 27 个同样大小的小正方体,从这些小正 方体中任取 1 个,则恰有两面涂有颜色的概率是( ) A. 4 27 B. 2 9 C. 1 3 D. 4 9 解析:共有 27 个小正方体,每条棱的中间位置上有一个是两个面涂有颜色的小正 方体,共有 12 个,所以 P=12 27 = 4 9 . 答案:D 5.若以连续掷两次均匀的骰子分别得到的点数 m,n 作为点 P 的坐标,则点 P 满足 x 2+y2≤16 的概率是 . 解析:连续掷两次均匀的骰子,得到点数 m,n 记作 P(m,n),共有 36 种情况,其中点 P(m,n)满足 x 2+y2≤16 的有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),共 8 种情况, 所以 P= 8 36 = 2 9

答案号 6.有20张卡片,每张卡片上分别标有两个连续的自然数k,k+1,其中k=0,1,2,…,19 从这20张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取 到标有9,10的卡片,则卡片上两个数的各位数字之和为9+1+0=10)不小于14”为 事件A,则P(A)=」 解析:从这20张卡片中任取一张,有 (0,1),(1,2),(2,3),(3,4),(4,5),(5,6),(6,7,(7,8),(8,9),(9,10),(10,11),(11,12),(12,13),13,14) ,(14,15),(15,16),(16,17),(17,18),(18,19),(19,20),共有20个样本点.卡片上两个数的 各位数字之和不小于14的样本点有(7,8),(8,9),(16,17),(17,18),(18,19),共5个,则 PA)品= 答案 7.某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表 (单位:人): 是否参加书法社团 是否参加演讲社团 参加书法社团 未参加书法社团 参加演讲社团 未参加演讲社团 30 (1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率: (2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学 A1,A2,A3,A4,A5,3名女同学B1,B2,B3.现从这5名男同学和3名女同学中各随机选 1人,求A1被选中且B1未被选中的概率 解(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人,故至少参 加上述一个社团的共有45-30=15(人),所以从该班随机选1名同学,该同学至少参 加上迷一个社团的概率为P=号 45 (2)从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的样本 点有 (A1,B1),(A1,B2),(A1,B3,(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2)(A3,B3,(A4,B1),(A4,B 2),(A4,B3),(A5,B1),(A5,B2),(A5,B3),共15个 根据题意,这些基本事件的出现是等可能的 事件“A1被选中且B1未被选中”所包含的基本事件有(A1,B2),(A1,B3),共2个 国此A被选中且B1未被选中的概率为P=号 挑战创新 某产品的三个质量指标分别为x,y,,用综合指标S=x+y+z评价该产品的等级若 S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量 指标列表如下:
答案: 2 9 6.有 20 张卡片,每张卡片上分别标有两个连续的自然数 k,k+1,其中 k=0,1,2,…,19. 从这 20 张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取 到标有 9,10 的卡片,则卡片上两个数的各位数字之和为 9+1+0=10)不小于 14”为 事件 A,则 P(A)= . 解析:从这 20 张卡片中任取一张,有 (0,1),(1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8),(8,9),(9,10),(10,11),(11,12),(12,13),(13,14) ,(14,15),(15,16),(16,17),(17,18),(18,19),(19,20),共有 20 个样本点.卡片上两个数的 各位数字之和不小于 14 的样本点有(7,8),(8,9),(16,17),(17,18),(18,19),共 5 个,则 P(A)= 5 20 = 1 4 . 答案: 1 4 7.某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表 (单位:人): 是否参加演讲社团 是否参加书法社团 参加书法社团 未参加书法社团 参加演讲社团 8 5 未参加演讲社团 2 30 (1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率; (2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学 A1,A2,A3,A4,A5,3 名女同学 B1,B2,B3.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求 A1 被选中且 B1 未被选中的概率. 解:(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有 30 人,故至少参 加上述一个社团的共有 45-30=15(人),所以从该班随机选 1 名同学,该同学至少参 加上述一个社团的概率为 P=15 45 = 1 3 . (2)从这 5 名男同学和 3 名女同学中各随机选 1 人,其一切可能的结果组成的样本 点有 (A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B 2),(A4,B3),(A5,B1),(A5,B2),(A5,B3),共 15 个. 根据题意,这些基本事件的出现是等可能的. 事件“A1 被选中且 B1 未被选中”所包含的基本事件有(A1,B2),(A1,B3),共 2 个. 因此 A1 被选中且 B1 未被选中的概率为 P= 2 15 . 挑战创新 某产品的三个质量指标分别为 x,y,z,用综合指标 S=x+y+z 评价该产品的等级.若 S≤4,则该产品为一等品.现从一批该产品中,随机抽取 10 件产品作为样本,其质量 指标列表如下:
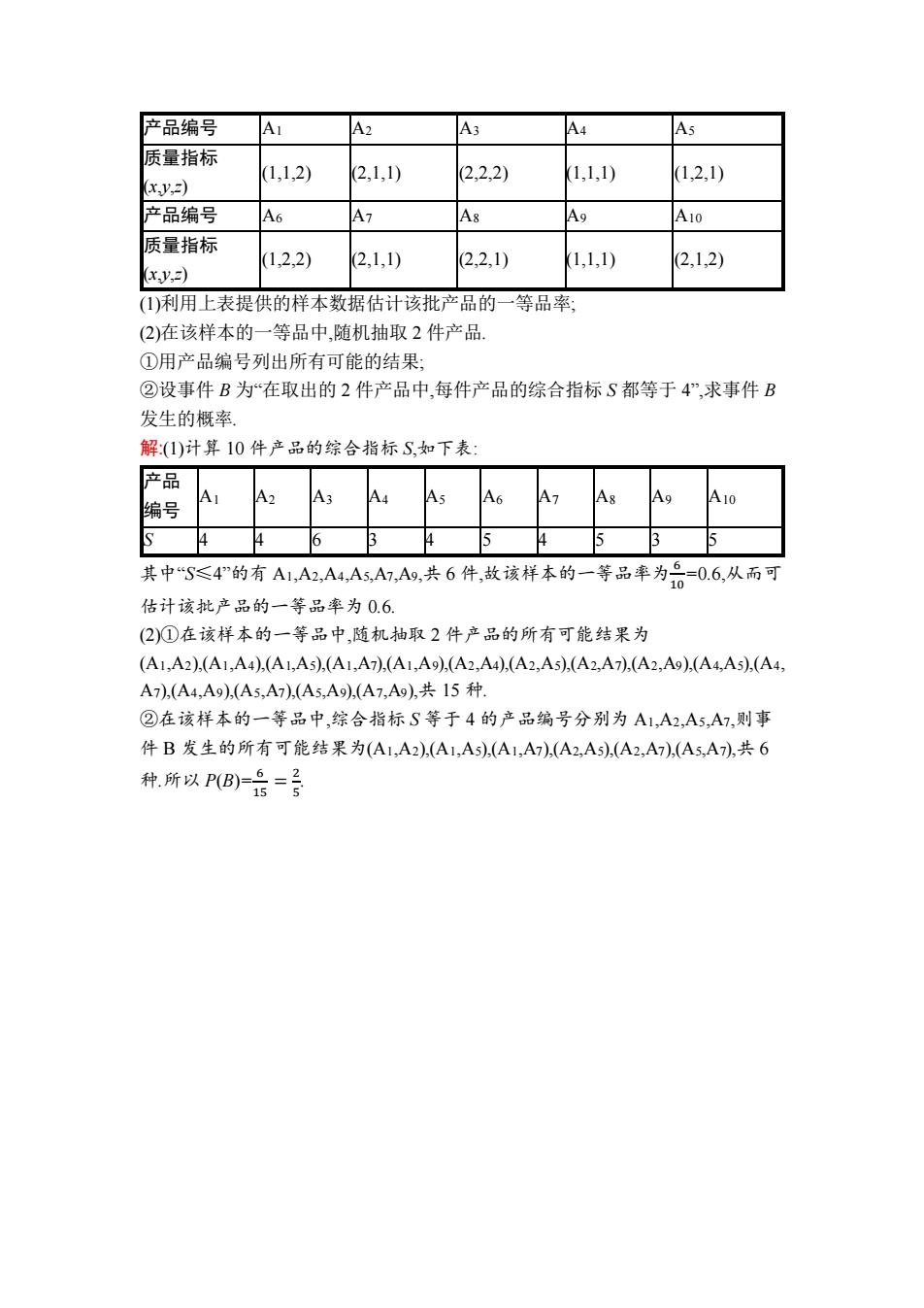
产品编号 A1 A2 A3 A4 A5 质量指标 1,1,2) (2,1,1) 2,2,2) (1,1,1) (1,2,1) y,2) 产品编号 A6 1A7 A8 A9 A10 质量指标 1,2,2) (2,1,1) (2,2,1) 1,1,1) (2,1,2) x,) (I)利用上表提供的样本数据估计该批产品的一等品率 (2)在该样本的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果: ②设事件B为在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B 发生的概率 解(1)计算10件产品的综合指标S,如下表: 产品 A6 A10 编号 S 其中“S≤4”的有A1,A2,A4,A5,A7,Ag,共6件,故该样本的一等品率为6=0.6,从而可 10 估计该批产品的一等品率为0.6. (2)①在该样本的一等品中,随机抽取2件产品的所有可能结果为 (A1,A2),(A1,A4),(A1,A5,(A1,A7),(A1,A9),(A2,A4),(A2,A5),(A2,A7),(A2,A9),(A4,A5,(A4, A7),(A4,A9),(A5,A7),(A5,A9),(A7,Ag),共15种 ②在该样本的一等品中,综合指标S等于4的产品编号分别为A1,A2,A5,A7,则事 件B发生的所有可能结果为(A1,A2),(A1,A5),(A1,A7),(A2,A5),(A2,A7),(A5,A7),共6 种,所以PB品=手
产品编号 A1 A2 A3 A4 A5 质量指标 (x,y,z) (1,1,2) (2,1,1) (2,2,2) (1,1,1) (1,2,1) 产品编号 A6 A7 A8 A9 A10 质量指标 (x,y,z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2) (1)利用上表提供的样本数据估计该批产品的一等品率; (2)在该样本的一等品中,随机抽取 2 件产品. ①用产品编号列出所有可能的结果; ②设事件 B 为“在取出的 2 件产品中,每件产品的综合指标 S 都等于 4”,求事件 B 发生的概率. 解:(1)计算 10 件产品的综合指标 S,如下表: 产品 编号 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 S 4 4 6 3 4 5 4 5 3 5 其中“S≤4”的有 A1,A2,A4,A5,A7,A9,共 6 件,故该样本的一等品率为 6 10 =0.6,从而可 估计该批产品的一等品率为 0.6. (2)①在该样本的一等品中,随机抽取 2 件产品的所有可能结果为 (A1,A2),(A1,A4),(A1,A5),(A1,A7),(A1,A9),(A2,A4),(A2,A5),(A2,A7),(A2,A9),(A4,A5),(A4, A7),(A4,A9),(A5,A7),(A5,A9),(A7,A9),共 15 种. ②在该样本的一等品中,综合指标 S 等于 4 的产品编号分别为 A1,A2,A5,A7,则事 件 B 发生的所有可能结果为(A1,A2),(A1,A5),(A1,A7),(A2,A5),(A2,A7),(A5,A7),共 6 种.所以 P(B)= 6 15 = 2 5