
全程设计 复习课 第2课时 复数
复习课 第2课时 复数

梳理•构建体系 归纳核心突破
梳理•构建体系 归纳•核心突破

导航 梳理构建体系 复数的实部 和虚部 复数的实数: 复数的概念之=a+bi(a,b∈R) 分类 虚数:,当a=0时,为纯虚数 复数相等:a+bi=c+di(a,b,c,d∈R),当且仅当a=c,b=d 数 复数之=a十bi(a,b∈R)与复平面内的点 建立了一一对应关系 复数的几 复数之=a+bi(a,b∈R)与复平面内的向量 建立了一一对应关系 何意义 复数之=a十bi(a,b∈R)的模:|z|= 复数之=a+bi(a,b∈R)的共轭复数:
导航 梳理•构建体系

导航 加法:(a+bi)+(c+di)= (a,b,c,d∈R), 复数的加、减运算 几何意义:复数的加法可以按照向量的加法来进行 复 及其几何意义 减法:(a+bi)-(c+di)= (a,b,,d∈R), 复数的四 几何意义:复数的减法可以按照向量的减法来进行 数 则运算 复数的乘、 乘法:(a十bi)(c+di)= (a,b,c,d∈R) 除运算 除法:(a+bi)÷(c+di)= (a,b,c,d∈R,且c+di≠0)
导航

导航 以x轴正半轴为始边、 为终边的一个角 辐角 复数的三 辐角主值:在 内的辐角,记作 角形式 三角表示:任何一个非零复数之=a十bi(a,b∈R)都可以表示成 复 ·复数的 的形式 三角形式 数 乘法:r1(cos01+isin01)Xr2(cos02+isin02)= 及其运算 复数三角形式 的乘、除运算 r (cos 01+isin 01) 除法:r2(cos0e+isin0:) (r2 (cos 02+isin 02)0)
导航

要点梳理 导 1复数的有关概念有哪些?请完成下表 内容 意义 备注 一 般地,当a与b都是实数 任意一个复数都由它的实 时,称a+bi为复数.复数一 部与虚部唯一确定,虚部为 复数 般用小写字母z表示,即= 0的复数实际上是一个实 的概 ①(a,b∈R),其中② 数.特别地,称虚部不为0 称为z的实部,③称为乙 的复数为虚数,称实部为0 的虚部 的虚数为纯虚数 复数 a+bi=c+di(a,b,c,d∈R)←→④ 相等
要点梳理 导航 1.复数的有关概念有哪些?请完成下表
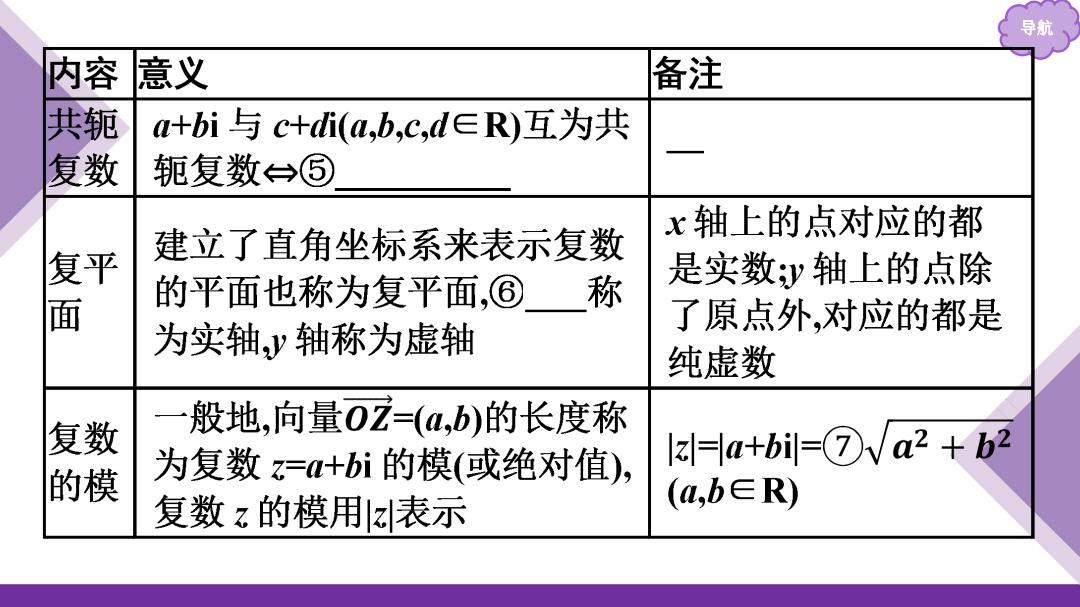
导航 内容 意义 备注 共轭 a+bi与c+di(a,b,c,d∈R)互为共 复数 轭复数→⑤ x轴上的点对应的都 建立了直角坐标系来表示复数 复平 的平面也称为复平面,⑥ 称 是实数y轴上的点除 了原点外,对应的都是 为实轴y轴称为虚轴 纯虚数 复数 般地,向量0Z=(a,b)的长度称 的模 为复数z=a+bi的模(或绝对值): lk=a+bi=⑦Va2+b2 复数z的模用z表示 (a,b∈R)
导航

导航 2.复数的几何意义是什么? 提示:复数集与平面直角坐标系的点集之间是一一对应的,复 数集与平面直角坐标系中以O为始点的向量组成的集合也是 一一对应的
导航 2.复数的几何意义是什么? 提示:复数集与平面直角坐标系的点集之间是一一对应的,复 数集与平面直角坐标系中以O为始点的向量组成的集合也是 一一对应的
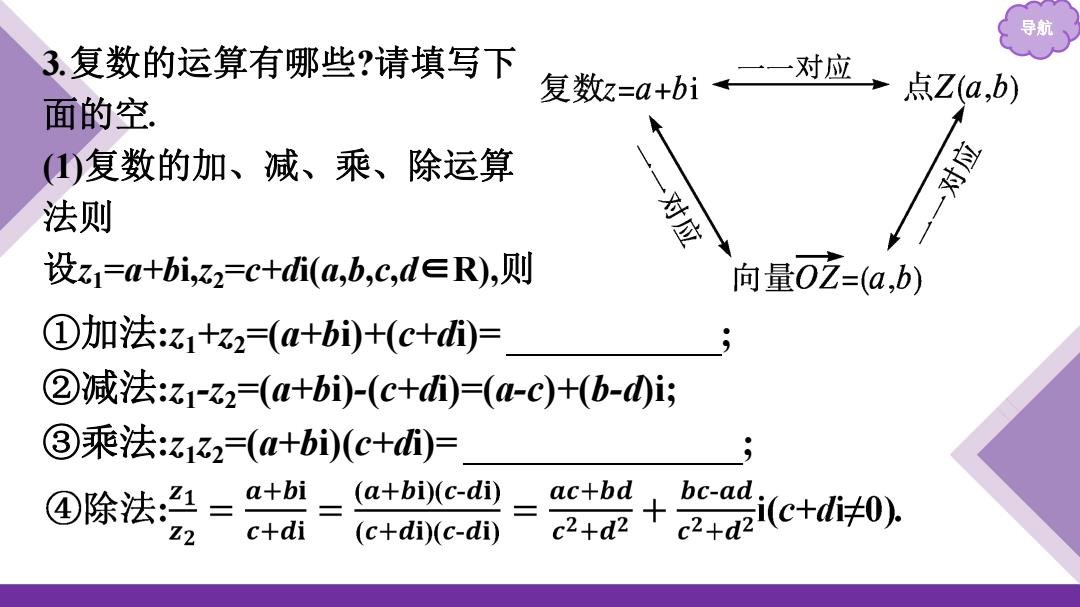
3.复数的运算有哪些?请填写下 面的空 复数z=a+b1二一对应 +点Z(a,b) ()复数的加、减、乘、除运算 对应 法则 对应 设z1=+biz2=c+di(a,b,C,d∈R),则 向量0Z=(a,b) ①加法:z1+z2=(a+bi)+(c+)= ②减法:z1z2=(a+bi)-(c+d)=(a-c)+(b-)i ③乘法:z12=(a+bi)(c+)= ④除法:1= a+bi (a+bi)(c-di) ac+bd bc-ad Z2 c+di (c+di)(c-di) c2+d2+ c2+2i(c+di40)
导航 3.复数的运算有哪些?请填写下 面的空. (1)复数的加、减、乘、除运算 法则 设z1=a+bi,z2=c+di(a,b,c,d∈R),则 ①加法:z1+z2=(a+bi)+(c+di)= (a+c)+(b+d)i ; ②减法:z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i; ③乘法:z1z2=(a+bi)(c+di)= (ac-bd)+(ad+bc)i ;

导 (2)复数加法的运算律 复数的加法满足交换律与结合律,即对任意复数z1,23,有 Z1+z2=2十z1,(亿1+z2)+73=71+(亿2+73) (3)复数加、减法的几何意义 ①复数加法的几何意义 如果复数z1,2所对应的向量分别为0Z,0Z2,则当0Z与0Z2不 共线时,以OZ1和OZ2为两条邻边作平行四边形OZZZ2,则 所对应的向量就是0Z
导航 (2)复数加法的运算律 复数的加法满足交换律与结合律,即对任意复数z1 ,z2 ,z3 ,有 z1+z2=z2+z1 ,(z1+z2)+z3=z1+(z2+z3). (3)复数加、减法的几何意义 ①复数加法的几何意义