
第六章平面向量初步 6.1平面向量及其线性运算 6.1. 1向量的概念 课后·训练提升 1.下列说法正确的是( A.向量必须用有向线段来表示 B.表示一个向量的有向线段是唯一的 C.有向线段AB和BA是同一向量 D.有向线段AB和BA的长度相等 答案D 2.若数轴上点A,B分别对应-1,2,则向量AB的长度是() A.-1 B.2 c.1 D.3 解析:AB=-1-2=3. 答案D 3.若AB=ADL,且BA=CD,则四边形ABCD的形状为() A.平行四边形B.矩形 C.菱形 D等腰梯形 解析:,BA=CD,.BA=CD,且AB∥CD, .四边形ABCD为平行四边形.又AB=AD, ∴.四边形ABCD为菱形. 答案:C 4.已知向量a,b是两个非零向量,A0,B0分别是与a,b同方向的单位向量,则以下 各式正确的是() A.AO=BO B.AO=BOAO=OB C.A0=OBD.AO与B0的长度相等 解析:单位向量的长度都为1. 答案D 5.如图,在圆0中,向量0B,0C,A0是(
第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.1 向量的概念 课后· 1.下列说法正确的是( ) A.向量必须用有向线段来表示 B.表示一个向量的有向线段是唯一的 C.有向线段𝐴𝐵⃗⃗⃗⃗⃗ 和𝐵𝐴⃗⃗⃗⃗⃗ 是同一向量 D.有向线段𝐴𝐵⃗⃗⃗⃗⃗ 和𝐵𝐴⃗⃗⃗⃗⃗ 的长度相等 答案:D 2.若数轴上点 A,B 分别对应-1,2,则向量𝐴𝐵⃗⃗⃗⃗⃗ 的长度是( ) A.-1 B.2 C.1 D.3 解析:|𝐴𝐵⃗⃗⃗⃗⃗ |=|-1-2|=3. 答案:D 3.若|𝐴𝐵⃗⃗⃗⃗⃗ |=|𝐴𝐷⃗⃗⃗⃗⃗ |,且𝐵𝐴⃗⃗⃗⃗⃗ = 𝐶𝐷⃗⃗⃗⃗⃗ ,则四边形 ABCD 的形状为( ) A.平行四边形 B.矩形 C.菱形 D.等腰梯形 解析:∵𝐵𝐴⃗⃗⃗⃗⃗ = 𝐶𝐷⃗⃗⃗⃗⃗ ,∴|𝐵𝐴⃗⃗⃗⃗⃗ |=|𝐶𝐷⃗⃗⃗⃗⃗ |,且 AB∥CD, ∴四边形 ABCD 为平行四边形.又|𝐴𝐵⃗⃗⃗⃗⃗ |=|𝐴𝐷⃗⃗⃗⃗⃗ |, ∴四边形 ABCD 为菱形. 答案:C 4.已知向量 a,b 是两个非零向量,𝐴𝑂⃗⃗⃗⃗⃗ , 𝐵𝑂⃗⃗⃗⃗⃗ 分别是与 a,b 同方向的单位向量,则以下 各式正确的是( ) A.𝐴𝑂⃗⃗⃗⃗⃗ = 𝐵𝑂⃗⃗⃗⃗⃗ B.𝐴𝑂⃗⃗⃗⃗⃗ = 𝐵𝑂⃗⃗⃗⃗⃗ 或𝐴𝑂⃗⃗⃗⃗⃗ = 𝑂𝐵⃗⃗⃗⃗⃗ C.𝐴𝑂⃗⃗⃗⃗⃗ = 𝑂𝐵⃗⃗⃗⃗⃗ D.𝐴𝑂⃗⃗⃗⃗⃗ 与𝐵𝑂⃗⃗⃗⃗⃗ 的长度相等 解析:单位向量的长度都为 1. 答案:D 5.如图,在圆 O 中,向量𝑂𝐵⃗⃗⃗⃗⃗ ,𝑂𝐶⃗⃗⃗⃗ ,𝐴𝑂⃗⃗⃗⃗⃗ 是( )

A有相同起点的向量 B.共线向量 C.模相等的向量 D.相等的向量 答案:C 6.如图,已知小正方形的边长为1,向量BA,BC的长度分别是 解析:根据题图易得BA=V32+5Z=V34,BC1=V32+2z=V13. 答案34,√13 7.己知a,b是任意两个向量,下列条件: ①a=b;②lal=lb:③a与b的方向相反;④a=0或b=0:⑤a与b都是单位向量 其中,使向量a与b平行的有 (只填序号) 解析:根据平行向量的定义可知①③④均能得到a∥b. 答案:①③④ 8.己知A,B,C是不共线的三点,向量m与向量AB是平行向量,与BC是共线向量,则 m= 解析:,AB与BC不平行,而m∥AB,且m∥BC, ∴.m=0 答案:0 9.如图,四边形ABCD为正方形,△BCE为等腰直角三角形,则 D (I)图中与AB共线的向量有 (2)图中与AB相等的向量有 (3)图中与AB的模相等的向量有 个 (4)图中与EC相等的向量是 解析(1).AE∥CD,.与AB共线的向量有CD,DC,BA,BE,EB,AE,EA,共7个 (2)由正方形ABCD和等腰直角三角形BCE知,AB=DC=BE (3)线段AD,DC,CB,BE,AB的长都相等,每一条线段可以产生两个模相等的向量,除 去向量AB,共有2×5-1=9(个(4)易证得DC一BE,.四边形CDBE是平行四边形, ..EC-BD.:.EC BD
A.有相同起点的向量 B.共线向量 C.模相等的向量 D.相等的向量 答案:C 6.如图,已知小正方形的边长为 1,向量𝐵𝐴⃗⃗⃗⃗⃗ , 𝐵𝐶⃗⃗⃗⃗ 的长度分别是 . 解析:根据题图易得|𝐵𝐴⃗⃗⃗⃗⃗ |=√3 2 + 5 2 = √34,|𝐵𝐶⃗⃗⃗⃗ |=√3 2 + 2 2 = √13. 答案:√34, √13 7.已知 a,b 是任意两个向量,下列条件: ①a=b;②|a|=|b|;③a 与 b 的方向相反;④a=0 或 b=0;⑤a 与 b 都是单位向量. 其中,使向量 a 与 b 平行的有 .(只填序号) 解析:根据平行向量的定义可知①③④均能得到 a∥b. 答案:①③④ 8.已知 A,B,C 是不共线的三点,向量 m 与向量𝐴𝐵⃗⃗⃗⃗⃗ 是平行向量,与𝐵𝐶⃗⃗⃗⃗ 是共线向量,则 m= . 解析:∵𝐴𝐵⃗⃗⃗⃗⃗ 与𝐵𝐶⃗⃗⃗⃗ 不平行,而 m∥𝐴𝐵⃗⃗⃗⃗⃗ ,且 m∥𝐵𝐶⃗⃗⃗⃗ , ∴m=0. 答案:0 9.如图,四边形 ABCD 为正方形,△BCE 为等腰直角三角形,则 (1)图中与𝐴𝐵⃗⃗⃗⃗⃗ 共线的向量有 个; (2)图中与𝐴𝐵⃗⃗⃗⃗⃗ 相等的向量有 个; (3)图中与𝐴𝐵⃗⃗⃗⃗⃗ 的模相等的向量有 个; (4)图中与𝐸𝐶⃗⃗⃗⃗ 相等的向量是 . 解析:(1)∵AE∥CD,∴与𝐴𝐵⃗⃗⃗⃗⃗ 共线的向量有𝐶𝐷⃗⃗⃗⃗⃗ ,𝐷𝐶⃗⃗⃗⃗⃗ ,𝐵𝐴⃗⃗⃗⃗⃗ , 𝐵𝐸⃗⃗⃗⃗ ,𝐸𝐵⃗⃗⃗⃗ , 𝐴𝐸⃗⃗⃗⃗ , 𝐸𝐴⃗⃗⃗⃗ ,共 7 个; (2)由正方形 ABCD 和等腰直角三角形 BCE 知,𝐴𝐵⃗⃗⃗⃗⃗ = 𝐷𝐶⃗⃗⃗⃗⃗ = 𝐵𝐸⃗⃗⃗⃗ ; (3)线段 AD,DC,CB,BE,AB 的长都相等,每一条线段可以产生两个模相等的向量,除 去向量𝐴𝐵⃗⃗⃗⃗⃗ ,共有 2×5-1=9(个);(4)易证得 DC BE,∴四边形 CDBE 是平行四边形, ∴EC BD,∴𝐸𝐶⃗⃗⃗⃗ = 𝐵𝐷⃗⃗⃗⃗
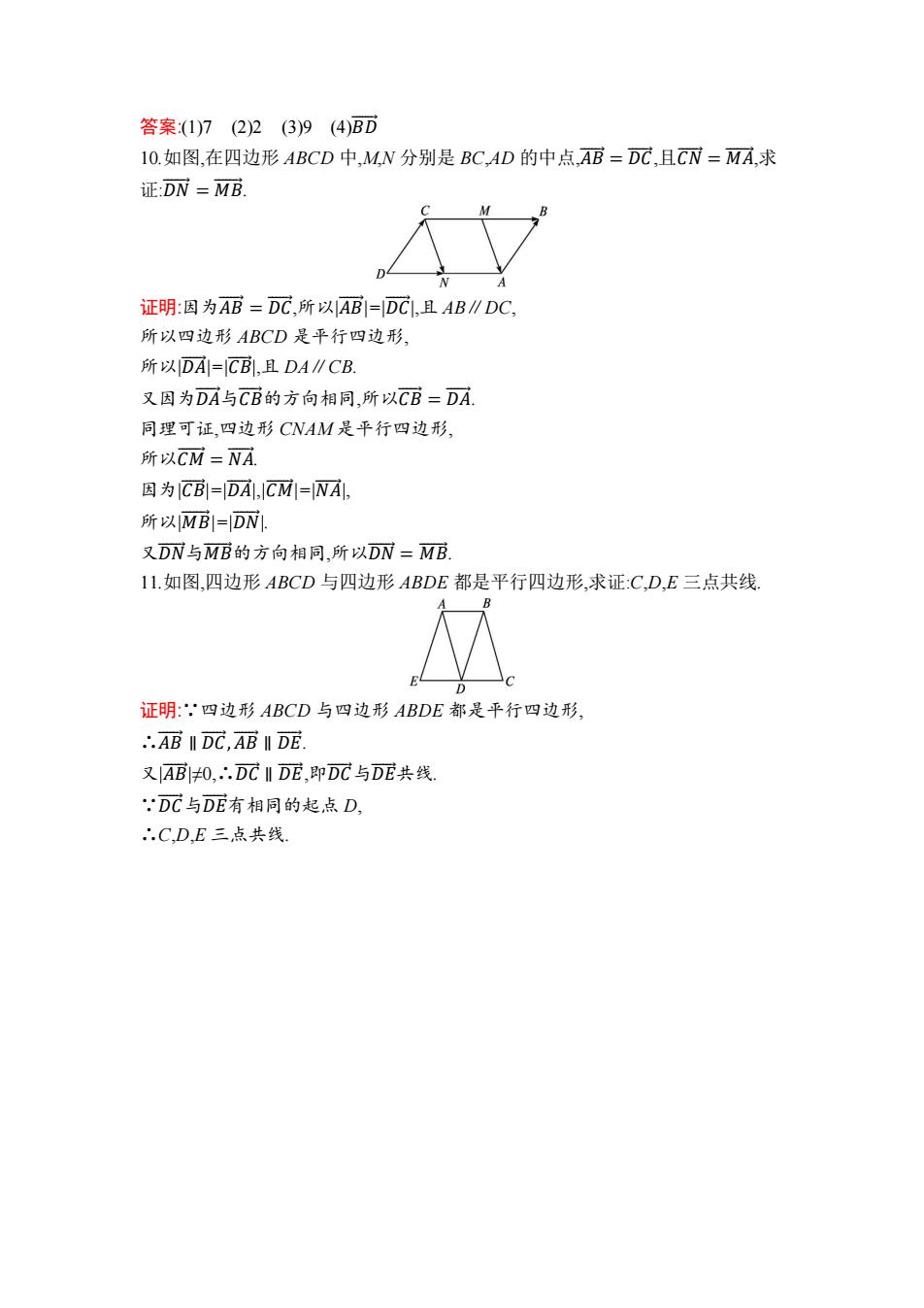
答案:(1)7(2)2(3)9(4)BD 10.如图,在四边形ABCD中,MN分别是BC,AD的中点,AB=DC,且CN=MA,求 证:DN=MB 证明:因为AB=DC,所以AB=DC,且AB∥DC, 所以四边形ABCD是平行四边形, 所以DA=CBL,且DA∥CB. 又因为DA与CB的方向相同,所以CB=DA 同理可证,四边形CNAM是平行四边形, 所以CM=NA 因为CB=DA,CM=NA, 所以MB=DN 又DN与MB的方向相同,所以DN=MB 11.如图,四边形ABCD与四边形ABDE都是平行四边形,求证:C,D,E三点共线 证明:,四边形ABCD与四边形ABDE都是平行四边形, ..AB II DC,AB II DE. 又AB0,.DC II DE,即DC与DE共线. DC与DE有相同的起点D, C,D,E三点共线
答案:(1)7 (2)2 (3)9 (4)𝐵𝐷⃗⃗⃗⃗ 10.如图,在四边形 ABCD 中,M,N 分别是 BC,AD 的中点,𝐴𝐵⃗⃗⃗⃗⃗ = 𝐷𝐶⃗⃗⃗⃗⃗ ,且𝐶𝑁⃗⃗⃗⃗⃗ = 𝑀𝐴 ⃗⃗⃗⃗⃗⃗ ,求 证:𝐷𝑁⃗⃗⃗⃗⃗ = 𝑀𝐵 ⃗⃗⃗⃗⃗⃗ . 证明:因为𝐴𝐵⃗⃗⃗⃗⃗ = 𝐷𝐶⃗⃗⃗⃗⃗ ,所以|𝐴𝐵⃗⃗⃗⃗⃗ |=|𝐷𝐶⃗⃗⃗⃗⃗ |,且 AB∥DC, 所以四边形 ABCD 是平行四边形, 所以|𝐷𝐴⃗⃗⃗⃗⃗ |=|𝐶𝐵⃗⃗⃗⃗ |,且 DA∥CB. 又因为𝐷𝐴⃗⃗⃗⃗⃗ 与𝐶𝐵⃗⃗⃗⃗ 的方向相同,所以𝐶𝐵⃗⃗⃗⃗ = 𝐷𝐴⃗⃗⃗⃗⃗ . 同理可证,四边形 CNAM 是平行四边形, 所以𝐶𝑀⃗⃗⃗⃗⃗ = 𝑁𝐴⃗⃗⃗⃗ . 因为|𝐶𝐵⃗⃗⃗⃗ |=|𝐷𝐴⃗⃗⃗⃗⃗ |,|𝐶𝑀⃗⃗⃗⃗⃗ |=|𝑁𝐴⃗⃗⃗⃗ |, 所以|𝑀𝐵 ⃗⃗⃗⃗⃗⃗ |=|𝐷𝑁⃗⃗⃗⃗⃗ |. 又𝐷𝑁⃗⃗⃗⃗⃗ 与𝑀𝐵 ⃗⃗⃗⃗⃗⃗ 的方向相同,所以𝐷𝑁⃗⃗⃗⃗⃗ = 𝑀𝐵 ⃗⃗⃗⃗⃗⃗ . 11.如图,四边形 ABCD 与四边形 ABDE 都是平行四边形,求证:C,D,E 三点共线. 证明:∵四边形 ABCD 与四边形 ABDE 都是平行四边形, ∴𝐴𝐵⃗⃗⃗⃗⃗ ∥ 𝐷𝐶⃗⃗⃗⃗⃗ , 𝐴𝐵⃗⃗⃗⃗⃗ ∥ 𝐷𝐸⃗⃗⃗⃗⃗ . 又|𝐴𝐵⃗⃗⃗⃗⃗ |≠0,∴𝐷𝐶⃗⃗⃗⃗⃗ ∥ 𝐷𝐸⃗⃗⃗⃗⃗ ,即𝐷𝐶⃗⃗⃗⃗⃗ 与𝐷𝐸⃗⃗⃗⃗⃗ 共线. ∵𝐷𝐶⃗⃗⃗⃗⃗ 与𝐷𝐸⃗⃗⃗⃗⃗ 有相同的起点 D, ∴C,D,E 三点共线