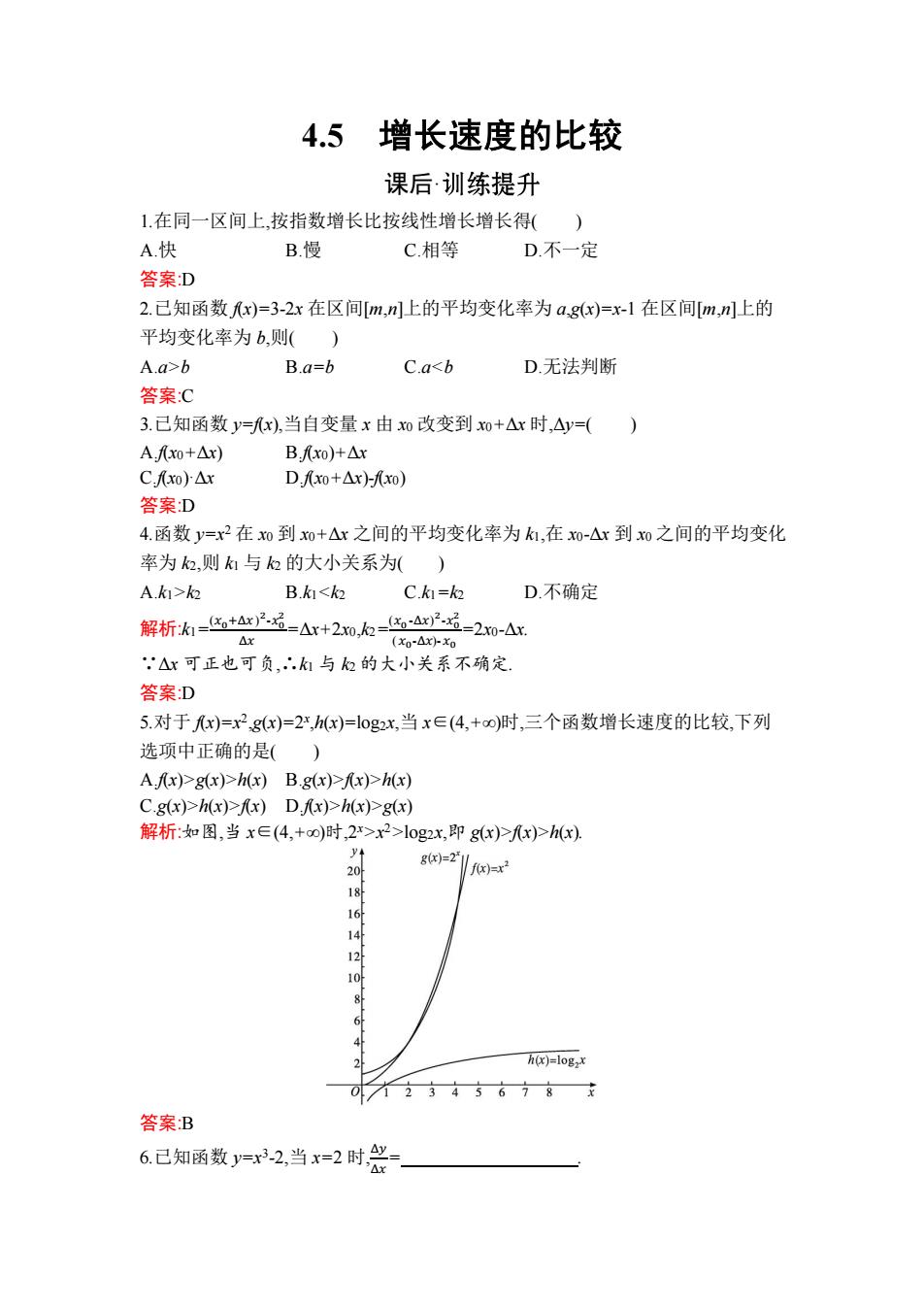
4.5 增长速度的比较 课后·训练提升 1.在同一区间上,按指数增长比按线性增长增长得( A.快 B.慢 C相等 D不一定 答案D 2.己知函数x)=3-2x在区间[m,n川上的平均变化率为a,g(x)=x-1在区间[m,n川上的 平均变化率为b,则( A.a>b B.a=b C.a2 B.kg(x)>h(x)B.g(x)Ax)>h(x) C.g(x)h(x)Ax)D.Ax)>h(x)>g(x) 解析:如图,当x∈(4,+oo)时,2r>x2>log2x,即gx)>x)>h(x) y g6c)=21l x)x 18 16 14 12 h(x)=log2x 答案B 6.己知函数y=x3-2,当x=2时,g= Ax
4.5 增长速度的比较 课后· 1.在同一区间上,按指数增长比按线性增长增长得( ) A.快 B.慢 C.相等 D.不一定 答案:D 2.已知函数 f(x)=3-2x 在区间[m,n]上的平均变化率为 a,g(x)=x-1 在区间[m,n]上的 平均变化率为 b,则( ) A.a>b B.a=b C.ak2 B.k1g(x)>h(x) B.g(x)>f(x)>h(x) C.g(x)>h(x)>f(x) D.f(x)>h(x)>g(x) 解析:如图,当 x∈(4,+∞)时,2x>x2>log2x,即 g(x)>f(x)>h(x). 答案:B 6.已知函数 y=x3 -2,当 x=2 时, Δ𝑦 Δ𝑥 =

解析:,△y=(2+△x)3-2-(23-2) =(2+△x)2(2+△x-8 =[4+4△x+(△x)2]2+△x)-8 =12△x+6(△x)2+(△x)3 .义=12+6△x+(△x2 △x 答案:(△x)P+6△x+12 7.经过研究,某个婴儿从出生到第24个月的体重变化图象如图所示,那么该婴儿 体重的平均变化率 较大.(填“第一年”或“第二年) Aw/kg 14.25------ 11.25 3.75 12 24阴 解析:由题图可知,第一年该婴儿体重的平均变化率为425375=0.625, 12-0 第二年该婴儿体重的平均变化率 为425-1125=0.25,又0.625>0.25,所以第一年的平均变化率较大 24-12 答案第一年 8.圆的面积S与其半径r的关系是S=πr2,r∈(0,+o,试求r∈[1,1+△r](△>0)时,S 的平均变化率 解:当r∈[1,1+△时, 圆面积S的平均变化率为g=1+Ar2严=+mAr+rn=2元+元△y Ar △r △T 9.已知函数x)=x+三分别计算x)在自变量x从1变到2和从3变到5时的平均 变化率,并判断在哪个区间上函数值变化得较快 解自变量x从1变到2时,函数)的平均变化率为2L=21+”= 21 1 2 自变量x从3变到5时,函数)的平均变化率为⑤@=5+(3+ 5-3 2 2= 15 国为<若所以函数)=x+在自变量x从3变到5时函数值变化得较快
解析:∵Δy=(2+Δx) 3 -2-(23 -2) =(2+Δx) 2 (2+Δx)-8 =[4+4·Δx+(Δx) 2 ](2+Δx)-8 =12·Δx+6(Δx) 2+(Δx) 3 , ∴ Δ𝑦 Δ𝑥 =12+6·Δx+(Δx) 2 . 答案:(Δx) 2+6Δx+12 7.经过研究,某个婴儿从出生到第 24 个月的体重变化图象如图所示,那么该婴儿 体重的平均变化率 较大.(填“第一年”或“第二年”) 解析:由题图可知,第一年该婴儿体重的平均变化率为11.25-3.75 12-0 =0.625, 第二年该婴儿体重的平均变化率 为 14.25-11.25 24-12 =0.25,又 0.625>0.25,所以第一年的平均变化率较大. 答案:第一年 8.圆的面积 S 与其半径 r 的关系是 S=πr 2 ,r∈(0,+∞),试求 r∈[1,1+Δr](Δr>0)时,S 的平均变化率. 解:当 r∈[1,1+Δr]时, 圆面积 S 的平均变化率为Δ𝑆 Δ𝑟 = π(1+Δ𝑟) 2 -π Δ𝑟 = π+2π·Δ𝑟+(Δ𝑟) 2π-π Δ𝑟 =2π+πΔr. 9.已知函数 f(x)=x+1 𝑥 ,分别计算 f(x)在自变量 x 从 1 变到 2 和从 3 变到 5 时的平均 变化率,并判断在哪个区间上函数值变化得较快. 解:自变量 x 从 1 变到 2 时,函数 f(x)的平均变化率为𝑓(2)-𝑓(1) 2-1 = 2+ 1 2 -(1+1) 1 = 1 2 ; 自变量 x 从 3 变到 5 时,函数 f(x)的平均变化率为𝑓(5)-𝑓(3) 5-3 = 5+ 1 5 -(3+ 1 3 ) 2 = 14 15 . 因为1 2 < 14 15 ,所以函数 f(x)=x+1 𝑥在自变量 x 从 3 变到 5 时函数值变化得较快