
全程设计 第1课时 两角和与差的正弦
第1课时 两角和与差的正弦

导航 课标定位素养阐释 1.能用两角和(差)的余弦公式及诱导公式导出两角和(差)的 正弦公式。 2.能利用公式解决简单的化简、求值等问题 3.加强逻辑推理、数学运算能力的培养
导航 课标定位 素养阐释 1.能用两角和(差)的余弦公式及诱导公式导出两角和(差)的 正弦公式. 2.能利用公式解决简单的化简、求值等问题. 3.加强逻辑推理、数学运算能力的培养

课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 两角和与差的正弦 【问题思考】 1.“sin(a+)=sina+sinp”对任意a,B成立吗? 提示:不成立 2.你能用a,B的三角函数表示sin(a+)吗? 提示:sin(a+f)=-cosE-(a+B)-cos(2a-l -cos(-)cos B+sin)sin B-sin acos Bcos asin B
导航 课前·基础认知 一、两角和与差的正弦 【问题思考】 1. “sin(α+β)=sin α+sin β”对任意α,β成立吗? 提示:不成立. 2.你能用α,β的三角函数表示sin(α+β)吗?

3.填表:两角和与差的正弦公式 导航、 名称 简记符号 公 式 使用条件 两角和 sin(a+B)= 的正弦 Sa+B ap∈R 两角差 sin(o-β= 的正弦 Sa-B ap∈R 4.做一做:(1)sin75°= (2)sin62°c0s2°-c0s62°sin2°= 答案62e
导航 3.填表:两角和与差的正弦公式 4.做一做:(1)sin 75° = ; (2)sin 62°cos 2°-cos 62°sin 2° =

导航 二、辅助角公式 【问题思考】 1.式子“sinx+cosx”能否化为Asin(x+p)的形式? 提示:能,sinx+cosx=V2sin(x+) 2.填空:fx)=asin x+bc0sx=Va2+b2sin(x+0)(a,b不同时为0), 共mi
导航 二、辅助角公式 【问题思考】 1.式子“sin x+cos x”能否化为Asin(x+φ)的形式?
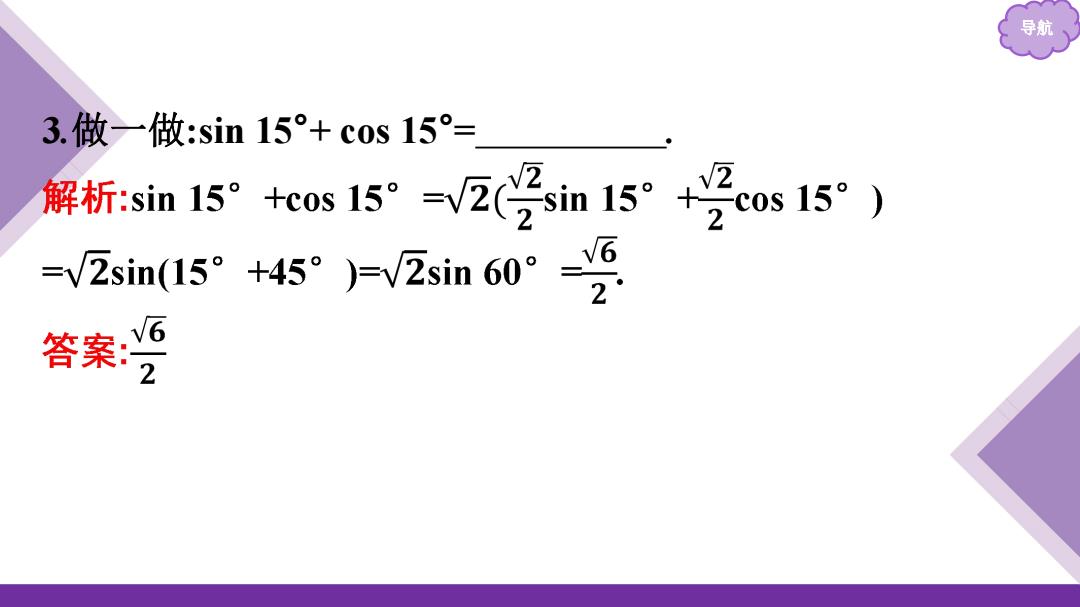
导航 3.做一做:sin15°+c0s15°= 解析sin15°0s15-V2受in15°+竖cos15) -V2sin(s”+45°)=v2sin60°_5 答案
导航 3.做一做:sin 15°+ cos 15°=

导 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (1)两角和与差的正弦公式中的角a,是任意的.( (2)存在a,∈R,使得sin(a-)=sina-sinP成立.() (3)对于任意a,B∈R,sin(a+p)=sina+sin都不成立.( (4)sin54°cos24°-sin36°sin24°=sin30°.(√)
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√” ,错 误的画“×” . (1)两角和与差的正弦公式中的角α,β是任意的.( √ ) (2)存在α,β∈R,使得sin(α-β)=sin α-sin β成立.( √ ) (3)对于任意α,β∈R,sin(α+β)=sin α+sin β都不成立.( × ) (4)sin 54°cos 24°-sin 36°sin 24° =sin 30° .( √ )

导航 课堂·重难突破 探究一给角求值问题 【例1】求值:(1)cos44°sin14°-sin44°cos14°; (2)(tan10°-V3)xcos10° sin50° 解原式=sin(14°-4°)户in(-30°)sin30°=号 (2)原式=(tan10°-tan60°)os10 sin10° sin60 c0s10° sin50° c0s10° c0S60° sin50° sin(-50°) c0S10° =-2. c0s10°c0s60°sin50°
导航 课堂·重难突破 探究一 给角求值问题 【例1】 求值:(1)cos 44°sin 14°-sin 44°cos 14°;

导期 反思感悟 1.含有非特殊角的三角求值问题,往往要按先整体、后局部的 原则.若整体可应用三角公式则整体变形,否则先各局部变形. 2.解决此类问题的一般途径有将非特殊角化为特殊角的和 (差)形式,化为正负相消的项消项求值,化简分子、分母的形 式进行约分等
导航 反思感悟 1.含有非特殊角的三角求值问题,往往要按先整体、后局部的 原则.若整体可应用三角公式则整体变形,否则先各局部变形. 2.解决此类问题的一般途径有将非特殊角化为特殊角的和 (差)形式,化为正负相消的项消项求值,化简分子、分母的形 式进行约分等