
全程设计 第2课时 两角和与差的正)
第2课时 两角和与差的正切

导航 课标定位素养阐释 1.能推导出两角和与差的正切公式 2.掌握两角和与差的正切公式及变形. 3.能利用公式进行简单的求值、化简等. 4加强逻辑推理能力和数学运算能力的培养
导航 课标定位 素养阐释 1.能推导出两角和与差的正切公式. 2.掌握两角和与差的正切公式及变形. 3.能利用公式进行简单的求值、化简等. 4.加强逻辑推理能力和数学运算能力的培养

课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航、 课前·基础认知 两角和与差的正切 【问题思考】 l.tan(a+p),tan(a-)能否用tana,tanP表示? 提示:能
导航 课前·基础认知 两角和与差的正切 【问题思考】 1.tan(α+β),tan(α-β)能否用tan α,tan β表示? 提示:能
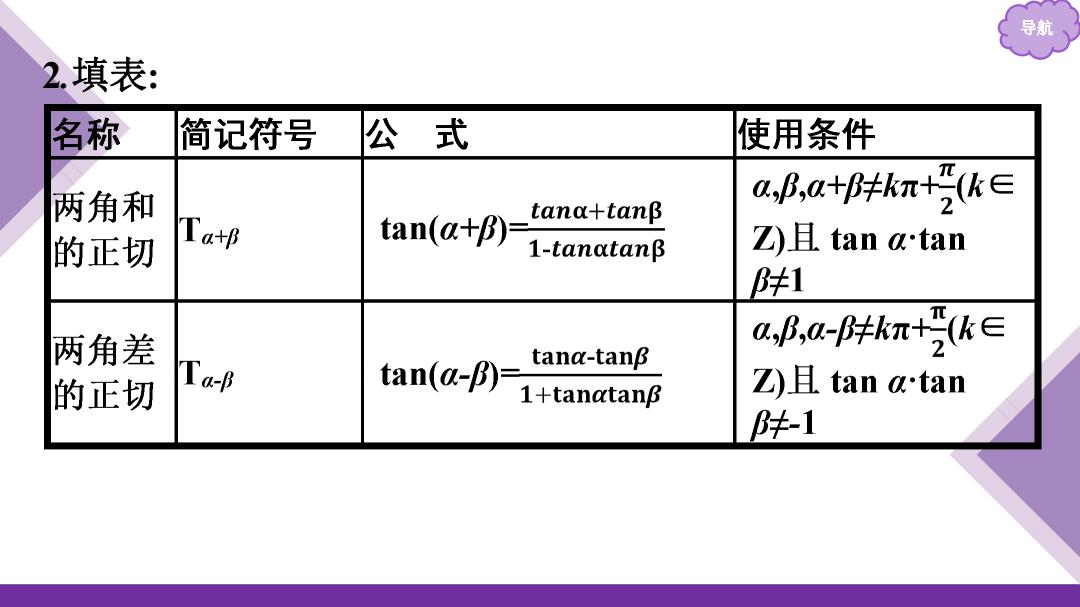
导航 2填表: 名称 简记符号 公式 使用条件 两角和 a,B,a+胖kπ+k∈ ana+tanβ 的正切 Ta+B tan(a+B)- -tanatanβ Z)且tan atan 1 两角差 a,B,a-km+k∈ 的正切 Ta-B tan(a-B)- tana-tanβ 1+tanatanB Z)且tan a'tan ≠-1
导航 2.填表:

导航 3.做一做:(1)tan15°= (2 tan15°-1 tan15°+1 答案:(12-V3(2号
导航

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” (1)存在a,B∈R,使tan(a+)=tana+tanB成立.( (2)对任意aB∈R,an(a+0 tancitanp 都成立.( 1-tanatanB 3ta(a+明na2等价于tan tan -tan(a+B)(1-tan atan B).( (④tan(+罗)可根据公式tan(a+直接展开.(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√” ,错 误的画“×”

导航 课堂·重难突破 探究一给角求值问题 【例1】求下列各式的值. (1)v3tan75° V3+tan75。; (2)tan23°+tan37°+v3tan23°tan37°. 分析:(1)将特殊值转化为特殊角的正切,逆用公式求解;(2)利 用tan(a+)的变形公式求解
导航 课堂·重难突破 探究一 给角求值问题 【例1】 求下列各式的值. 分析:(1)将特殊值转化为特殊角的正切,逆用公式求解;(2)利 用tan(α+β)的变形公式求解

导航 、1-V3tan75° 解:(13+tan75° tan75o 1+an75 127560-7s") =tan(-45°)=-tan45°=-1. (2):tan(23°+37°)=tan60° 0a=V3 .tan23°+tan37°=V3(1-tan23°tan37°), .:原式=V3(1-tan23°tan37°)+v3tan23°tan37°=3
导航

导航 反思感悟 在同一式子中,同时出现ana+tanB(tana-tan)和tan atan阝, 可应用tan(a+)或tan(a-)的变形公式求解
导航 反思感悟 在同一式子中,同时出现tan α+tan β(tan α-tan β)和tan αtan β, 可应用tan(α+β)或tan(α-β)的变形公式求解