
全程设计 7.4 数学建模活动:周期现象的描述
7.4 数学建模活动: 周期现象的描述

导航 课标定位 素养阐释 1.了解常见的周期现象. 2.能借助于合适的仪器,采集数据,建立数学模型,分析研究周 期现象 3.加强数据分析、数学运算、逻辑分析能力的培养
导航 课标定位 素养阐释 1.了解常见的周期现象. 2.能借助于合适的仪器,采集数据,建立数学模型,分析研究周 期现象. 3.加强数据分析、数学运算、逻辑分析能力的培养

导月 数学建模 完整的数学建模活动一般要经历选题、开题、做题、结题四 个过程 1选题是指根据要求选定合适的研究对象的过程 2.开题是指讨论与确定建模步骤的过程. 3.做题是指按照讨论的步骤进行实际建模的过程 4.结题是指总结与交流的过程
导航 一、数学建模 完整的数学建模活动一般要经历选题、开题、做题、结题四 个过程. 1.选题是指根据要求选定合适的研究对象的过程. 2.开题是指讨论与确定建模步骤的过程. 3.做题是指按照讨论的步骤进行实际建模的过程. 4.结题是指总结与交流的过程

二、建立数学模型解决实际问题 导航 【例题】[发现问题,提出问题] 一个地区在不同日子中白昼的时长是不同的,下表是某地一 年中10天测量的白昼时长统计表(时间近似到0.1h). 日期 1月 2月 B月 4月 5月 6月 8月 9月 10月 12月 1日 28日 21日 27日 6日 21日 13日 20日 25日 21日 日期位 置编号 59 180 117 126 172 225 263 298 355 x 白昼时 长yh 5.6 10.2 12.4 16.4 17.3 19.4 16.4 12.4 8.5 5.4
导航 二、建立数学模型解决实际问题 【例题】 [发现问题,提出问题] 一个地区在不同日子中白昼的时长是不同的,下表是某地一 年中10天测量的白昼时长统计表(时间近似到0.1 h). 日期 1月 1日 2月 28日 3月 21日 4月 27日 5月 6日 6月 21日 8月 13日 9月 20日 10月 25日 12月 21日 日期位 置编号 x 1 59 80 117 126 172 225 263 298 355 白昼时 长y/h 5.6 10.2 12.4 16.4 17.3 19.4 16.4 12.4 8.5 5.4
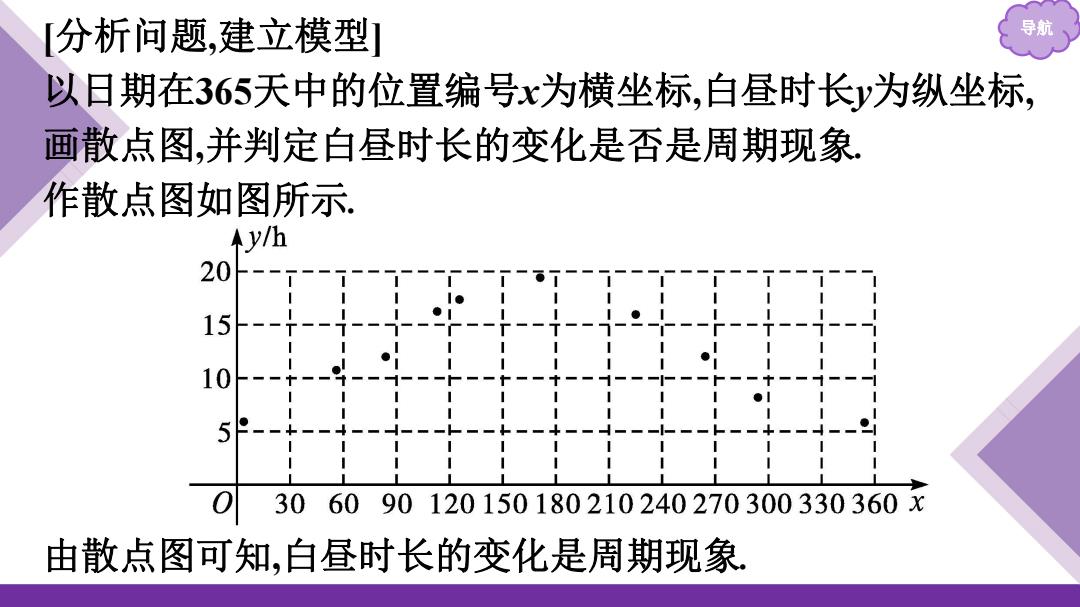
[分析问题,建立模型] 以日期在365天中的位置编号x为横坐标,白昼时长y为纵坐标, 画散点图,并判定白昼时长的变化是否是周期现象, 作散点图如图所示 Ay/h 20 15 10 5 30 6090120150180210240270300330360x 由散点图可知,白昼时长的变化是周期现象
导航 [分析问题,建立模型] 以日期在365天中的位置编号x为横坐标,白昼时长y为纵坐标, 画散点图,并判定白昼时长的变化是否是周期现象. 作散点图如图所示. 由散点图可知,白昼时长的变化是周期现象

建立模型,分析求解 估计该地区一年中有多少天白昼时长大于15.9h;估计该地区 明年6月21日的白昼时长是多少 解:因为从4月27日至8月13日的白昼时长都超过15.9h,所以 该地区一年中白昼时长超过15.9h的大约有 4+31+30+31+13=109(天). 该地区明年6月21日白昼时长约是19.4h
导航 [建立模型,分析求解] 估计该地区一年中有多少天白昼时长大于15.9 h;估计该地区 明年6月21日的白昼时长是多少. 解:因为从4月27日至8月13日的白昼时长都超过15.9 h,所以 该地区一年中白昼时长超过15.9 h的大约有 4+31+30+31+13=109(天). 该地区明年6月21日白昼时长约是19.4 h

导期 反思感悟 周期现象的判断方法有: ()定义法.即利用周期现象的定义进行判断,判断的关键是看 现象是不是周期性地重复出现. (2)图象法.即画出图象(大多为散点图),从图象的变化规律中 判断是不是周期现象 3)特例法.当否定某现象不具有周期现象时,也可列举出一个 特殊数、特殊位置、特殊情况等
导航 反思感悟 周期现象的判断方法有: (1)定义法.即利用周期现象的定义进行判断,判断的关键是看 现象是不是周期性地重复出现. (2)图象法.即画出图象(大多为散点图),从图象的变化规律中 判断是不是周期现象. (3)特例法.当否定某现象不具有周期现象时,也可列举出一个 特殊数、特殊位置、特殊情况等

【变式训练】游乐场中的摩天轮逆时针匀速旋转,其中心0 距地面是40.5m,半径是40m,若你从最低点处登上摩天轮,则 你与地面的距离将随时间变化,5min后到达最高点.在你登上 摩天轮时开始计时,请解答下列问题. ()能求出你与地面的距离y与时间t的函数解析式吗? (2)当你登上摩天轮8min后,你与地面的距离是多少? (3)当你第1次距地面30.5m时,用了多少时间? (4)当你第4次距地面30.5m时,用了多少时间? 分析:因为从最低点到最高点的变换具有周期性,所以可以用 y=Asin(ωt什p)+b作为函数模型
导航 【变式训练】 游乐场中的摩天轮逆时针匀速旋转,其中心O 距地面是40.5 m,半径是40 m.若你从最低点处登上摩天轮,则 你与地面的距离将随时间变化,5 min后到达最高点.在你登上 摩天轮时开始计时,请解答下列问题. (1)能求出你与地面的距离y与时间t的函数解析式吗? (2)当你登上摩天轮8 min后,你与地面的距离是多少? (3)当你第1次距地面30.5 m时,用了多少时间? (4)当你第4次距地面30.5 m时,用了多少时间? 分析:因为从最低点到最高点的变换具有周期性,所以可以用 y=Asin(ωt+φ)+b作为函数模型

解:(1)如图,O是摩天轮轮心,作ON垂直地面于点N,交摩天轮 于点P,ON=40.5m,OP=40m.由题意可知,当=0时,你登上摩天 轮,位于点P,经过tmin,旋转到点P1处,点P到地面的距离为 PM.作PQ⊥OP于点Q. 因为人从最低点旋转到最高点需5min, 所以摩天轮的旋转速度为Frad/min, 经过1时摩天轮炭转的角度是导rad,即∠P0N骨rad 由图不难看出y=P1M=ON-OQ=40.5-OP1c0s∠P1O9 =40.5-40c0sg=40.5+40sin(gt-2) 函数J=40sin(t)+40.5即为所求函数的解析式
解 导航 :(1)如图,O是摩天轮轮心,作ON垂直地面于点N,交摩天轮 于点P,ON=40.5 m,OP=40 m.由题意可知,当t=0时,你登上摩天 轮,位于点P,经过t min,旋转到点P1处,点P1到地面的距离为 P1M=y.作P1Q⊥OP于点Q

导航 2)令t8,得=40sin(得×8- +40.5≈28.1, 即登上摩天轮8min后与地面的距离约为28.1m. ③)令Jy=30.5,得40sin(写t-)-10, 即c0s=0.25,得2.1, 即你第1次距地面30.5m时,用了约2.1min. (4)你第4次距地面30.5m时,用了20-2.1=17.9(min)
导航