
全程设计 习题果一一三角函数的求值问题
习题课——三角函数的求值问题

导航 课标定位素养阐释 1.掌握三角函数的有关公式及其变形 2.能灵活应用公式解决三角函数的求值问题 3.加强逻辑推理能力和数学运算能力的培养
导航 课标定位 素养阐释 1.掌握三角函数的有关公式及其变形. 2.能灵活应用公式解决三角函数的求值问题. 3.加强逻辑推理能力和数学运算能力的培养

课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 常用的公式或变形 【问题思考】 1.填空:(1)1+c0s= ,1-c0s0a= (2)1+sin a-(sin+cos ,I-sin a-(sin cos a (3)tan sina 2-1+c0s@ 1-cosa sing
导航 课前·基础认知 常用的公式或变形 【问题思考】
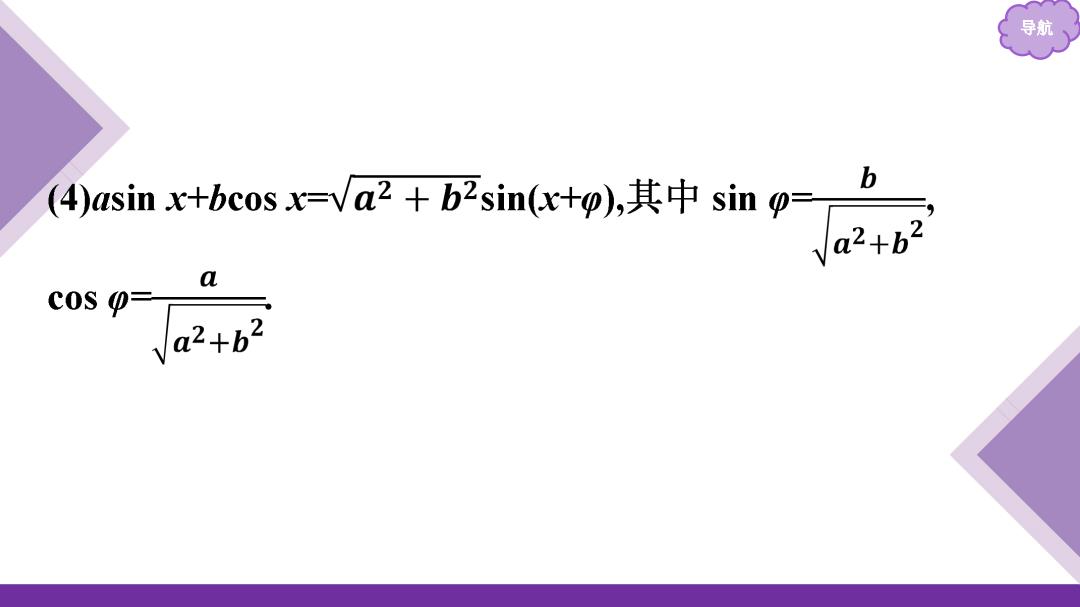
导航 4asin+bes.x-va+bsin6wT其巾sin2+ b a cos p= Ya2+b2
导航

导航 2.做一做:(1)sin15°.Vos15°= (2)若a终边上一点P(-1,2),则cos2a-3 sin acos a= 解析:(0原式=2in15°号cs15°)片2sn(15°60°) =-2sin45°=.V2. (2)由题意知,tana=-2, cos?a-3sin acos acos2a-3sinacosa = 1-3tang 1-3×(-2) 7 sin2a+cos2a tan2a+1 (-2)2+1 答案:()-V2(2号
导航 2.做一做:(1)sin 15°- cos 15°= ; (2)若α终边上一点P(-1,2),则cos2α-3sin αcos α=

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”, 0若ana号则sinu青cosa( 2)若a∈(π2x,则L-co+-sin( 2 3)当5<03os0君时sin9=( (4)公式asin+bcos x=Va2+b2sin(+p)中,p的取值与a,b的 值有关.()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√” ,错 误的画“×”

导航 课堂·重难突破 探究一给角求值问题 【例1】求值:(1 2sin235°-1 cos10°-V3sin10°y V3 1 (2 cos10°-sin170° 分析:应用公式,转化为特殊角的三角函数求值或将非特殊角 消去
导航 课堂·重难突破 探究一 给角求值问题 分析:应用公式,转化为特殊角的三角函数求值或将非特殊角 消去

导月 解:(1)原式 2sin235°-1 -C0s70° 1 2(2cos10°-号sin10 2c0s70° 2 (2)原式= 3 1 V3sin10°-cos10° c0s10° sin10° sin10°cos10° 2sin(10°-30° 2= -2sin20° 二-4. 23in20 1 sin20 反思感悟 解给角求值问题,就是想方设法将非特殊角转化为特殊角或 将非特殊角消去,从而达到化简求值的目的.求解时应灵活选 用三角公式,同时注意公式的正用、逆用和变形应用
导航 反思感悟 解给角求值问题,就是想方设法将非特殊角转化为特殊角或 将非特殊角消去,从而达到化简求值的目的.求解时应灵活选 用三角公式,同时注意公式的正用、逆用和变形应用

导航 【变式训练1】求值:2sin47°-v3sin17° c0s17° 解:原式=2xsin47°-sin17°cos30° c0S17 -2xsin(17°+30°)sin17°cos30° C0S17° =2sin30°=1
导航