
全程设计 8.1.2 向量数量积的运算律
8.1.2 向量数量积的运算律

导航 课标定位 素养阐释 1.掌握向量数量积的运算律 2.能根据运算律解决一些向量数量积的运算问题 3.加强逻辑推理能力和数学运算能力的培养」
导航 课标定位 素养阐释 1.掌握向量数量积的运算律. 2.能根据运算律解决一些向量数量积的运算问题. 3.加强逻辑推理能力和数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 向量数量积的运算律 【问题思考】 1.实数的乘法运算满足交换律、结合律和分配律,向量的数量 积运算中,是否也有类似的性质? 提示:有
导航 课前·基础认知 向量数量积的运算律 【问题思考】 1.实数的乘法运算满足交换律、结合律和分配律,向量的数量 积运算中,是否也有类似的性质? 提示:有
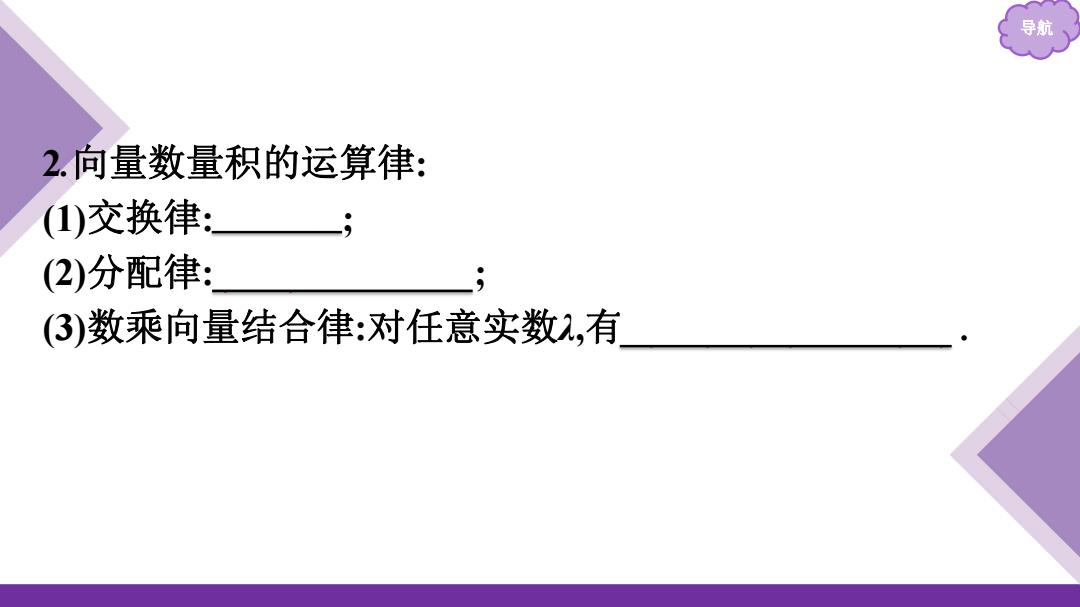
导航 2.向量数量积的运算律: (1)交换律: (2)分配律: (3)数乘向量结合律:对任意实数2,有
导航 2.向量数量积的运算律: (1)交换律:a·b=b·a; (2)分配律:(a+b)·c=a·c+b·c; (3)数乘向量结合律:对任意实数λ,有λ(a·b)=(λa)·b=a·(λb)

导航 3.做一做:已知点A,B,C满足AB=3,BC=4,CA=5,则AB BC+BC.CA+CA·AB的值是( A.-25 B.25 C.-24 D.24 解析:由已知,AB2+BC2=CA2,.:AB⊥BC .·原式=0+CA(AB+BC)=CA·AC=-CA2=-25. 答案:A
导航 答案:A

导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X”. (1)无论a,b是何向量,ab与ba必相等.( (2)1al2-lb12=(a+b)(a-b).( (3)(ab)c=a(bc).()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√” ,错 误的画“×” . (1)无论a,b是何向量,a·b与b·a必相等.( √ ) (2)|a|2-|b|2=(a+b)·(a-b).( √ ) (3)(a·b)·c=a·(b·c).( × )

导航 课堂·重难突破 探究一向量数量积运算律的应用 【例1】已知a与b的夹角0=150°,且al=3,b=4,求(a+b)(a-2b) 分析:根据向量数量积的运算律求解即可. 解:(a+b)(a-2b)=a2-ab-2b2 -a2-allblcos 0-2 b2 =9-3X4Xc0s150°-2X42 =-23+6V3
导航 课堂·重难突破 探究一 向量数量积运算律的应用 【例1】 已知a与b的夹角θ=150° ,且|a|=3,|b|=4,求(a+b)·(a-2b). 分析:根据向量数量积的运算律求解即可. 解:(a+b)·(a-2b)=a2-a·b-2b2 =|a|2-|a||b|cos θ-2|b|2 =9-3×4×cos 150°-2×42

了延伸探究 导航 在本例中,求a+2b的值. 解:,1a+2b2=(a+2b)2=a2+4b2+4ab =32+4X42+4X3X4Xc0s150° =9+64-24V3=73-24V3, la+2b=73-24v3. 反思感悟 根据数量积的运算律,向量的加、减与数量积的混合运算类 似于多项式的乘法运算
导航 在本例中,求|a+2b|的值. 解:∵|a+2b|2=(a+2b) 2=a2+4b2+4a·b =32+4×42+4×3×4×cos 150° 反思感悟 根据数量积的运算律,向量的加、减与数量积的混合运算类 似于多项式的乘法运算

导航 【变式训练1】已知a=4,b=5,且向量a与b的夹角为60°,则 2a+3b)(3a-2b)= 解析:(2a+3b)(3a-2b)=6a2+5ab-6b2 =6X16+5X4X5X2-6X25=-4. 答案:-4
导航 【变式训练1】 已知|a|=4,|b|=5,且向量a与b的夹角为60° ,则 (2a+3b)·(3a-2b)= . 解析:(2a+3b)·(3a-2b)=6a2+5a·b-6b2 =6×16+5×4×5× -6×25=-4. 答案:-4