
全程设计 8.2.3 倍角公式
8.2.3 倍角公式

导月 课标定位 素养阐释 1.理解二倍角公式的推导过程,知道倍角公式与和角公式之间 的内在联系 2.掌握二倍角的正弦、余弦、正切公式,并能运用这些公式进 行简单的恒等变换 3.加强数学运算、逻辑推理能力的培养
导航 课标定位 素养阐释 1.理解二倍角公式的推导过程,知道倍角公式与和角公式之间 的内在联系. 2.掌握二倍角的正弦、余弦、正切公式,并能运用这些公式进 行简单的恒等变换. 3.加强数学运算、逻辑推理能力的培养
课前·基础认知 课堂·重难突破 随堂训练 规范解答
规 范 解 答 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 倍角公式 【问题思考】 1.用a的三角函数如何表示sin2a,cos2a,tan2a? 提示:将2a看作a+α,利用两角和的三角公式展开整理即可.如 cos 2a=cos(a+a)=cos acos a-sin asin a=cos2a-sin2a
导航 课前·基础认知 倍角公式 【问题思考】 1.用α的三角函数如何表示sin 2α,cos 2α,tan 2α? 提示:将2α看作α+α,利用两角和的三角公式展开整理即可.如 cos 2α=cos(α+α)=cos αcos α-sin αsin α=cos 2α-sin2α

导航、 2填表 (1)倍角公式: 记 法 公 式 sin 2a= Cia cos 2a= 2tana T2a tan 2a= 1-tan2a
导航 2.填表. (1)倍角公式:

导航 (2)公式变形: ① 变形 cos 2a= sin2a= 1-cos 2a 2 cos 2a=cos2a-sin2a 变形 1+cos 2a cos 2a= cos2a= 2 1 sin acos a-zsin 2a,cos a= in2a sina ③1±sin2a=
导航 (2)公式变形: ① ③1±sin 2α= (sin α±cos α) 2
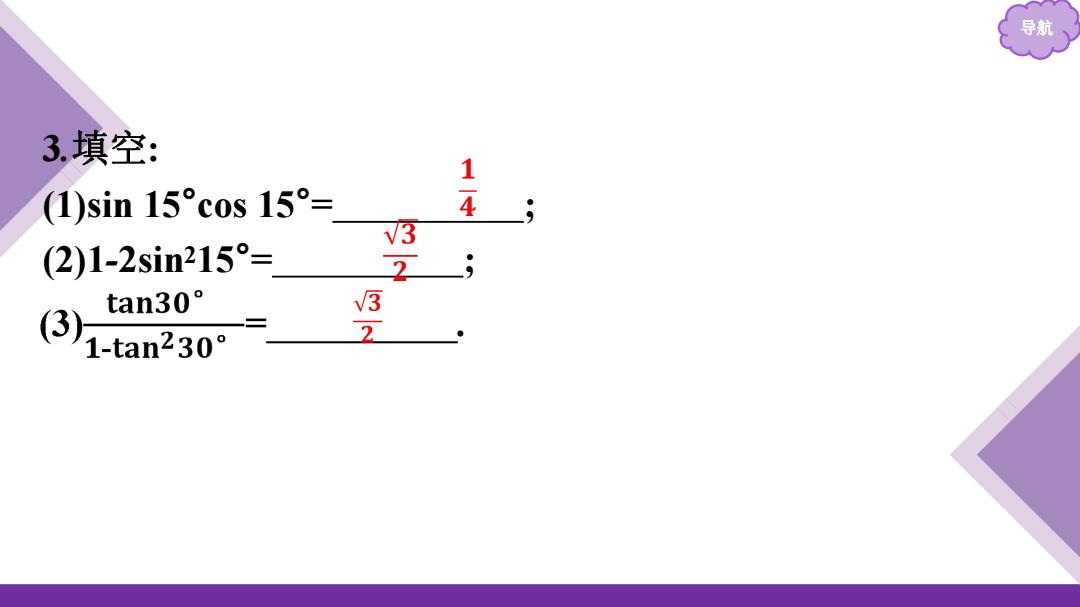
导航 3填空: 1 (1)sin15°cos15°= 4 V3 (2)1-2sin215°= 2 tan30° 3 (3 -三 1-tan230° 2
导航 3.填空: (1)sin 15°cos 15°= ; (2)1-2sin215°= ;

导 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错 误的画“X” ()二倍角的正弦、余弦、正切公式的适用范围是任意角. (2)存在角a,使得sin2a=2sina成立.( 2tana (3)对任意角a,总有tan2a=1-tan2a .( (4)不存在角a,使c0s2=2c0sa.()
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√” ,错 误的画“×” . (1)二倍角的正弦、余弦、正切公式的适用范围是任意角. ( × ) (2)存在角α,使得sin 2α=2sin α成立.( √ ) (3)对任意角α,总有tan 2α= .( × ) (4)不存在角α,使cos 2α=2cos α.( × )

导航 课堂·重难突破 探究一给角求值 【例1】求下列各式的值. 2tan150° (0 1-tan2150° (2)sin10°sin30°sin50°sin70°; (3) in50°(1+v3tan10°)+cos20° sin80°√1+c0s20°
导航 课堂·重难突破 探究一 给角求值 【例1】 求下列各式的值

导航 分析:(1)逆用二倍角的正切公式求解.(2)先将sin10°sin30°sin 50°sin70°变换为 ni0co2年将9、分母都乘 c0s10°,反复逆用二倍角的正弦公式即可得解.(3)先切化弦,再 综合应用和角、差角公式及二倍角公式求解
导航 分析:(1)逆用二倍角的正切公式求解.(2)先将sin 10°sin 30°sin 50°sin 70°变换为 ,再将分子、分母都乘 cos 10° ,反复逆用二倍角的正弦公式即可得解.(3)先切化弦,再 综合应用和角、差角公式及二倍角公式求解