
全程设计 习题果一一三角函数的性质与图象
习题课——三角函数的性质与图象

导航 课标定位 素养阐释 1.能画出y=sinx,y=cosx,y=tan x.y=Asin(wx+p)(A≠0)的图象. 2.掌握图象的变换规律及函数的性质. 3.能根据三角函数的图象及性质解决一些简单问题 4加强直观想象、逻辑推理能力和数学运算能力的培养
导航 课标定位 素养阐释 1.能画出y=sin x,y=cos x,y=tan x,y=Asin(ωx+φ)(A≠0)的图象. 2.掌握图象的变换规律及函数的性质. 3.能根据三角函数的图象及性质解决一些简单问题. 4.加强直观想象、逻辑推理能力和数学运算能力的培养
课前·基础认知 课堂·重难突破 随堂训练 思想方法
思 想 方 法 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 函数y=sinx,y=cosK,y=tanx的性质与图象 【问题思考】 1.填空:(山函数=tanx的定义域为[xx≠km+2,k∈Z为 (2)函数y=sinx,y=cosx的值域为 (3)y=cosx的单调递减区间是 y=tanx的单 调递增区间是 ,周期是; (4)函数y=tanx的图象对称轴,其对称中心的坐标为
导航 课前·基础认知 一、函数y=sin x,y=cos x,y=tan x的性质与图象 【问题思考】

导航 2.做一做:(1)若函数y=3cosx的周期为,则实数a为 (2)函数y=M-2sinx的最小值为 (3)函数y=tanx满足tanx≤0的单调递增区间为 答案:()±4(2)M-23km-2,kπ(k∈Z☑
导航 2.做一做:(1)若函数y=-3cos ax的周期为 ,则实数a为 ; (2)函数y=M-2sin x的最小值为 ; (3)函数y=tan x满足tan x≤0的单调递增区间为

二、Jy=Asin(ox+p)+k(或y=Ac0s(wx+p)+k,A,w,p,k∈R且 A,0≠0)的图象 【问题思考】 1.填空:(1)用五点法”作y=Asin(wx+p)+k的图象时,令wx+p 取的五个值依次为_受-受一 3π (2)通过变换由y=cosx的图象作y=Acos(ωx+p)+k的图象时, 若平移的量为个单位,则为先 变换后 变换。 2.做一做:将=c0s(2x的图象向_平移个单位,得到 y=cos2x的图象
导航 二、y=Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k,A,ω,φ,k∈R且 A,ω≠0)的图象 【问题思考】

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√,错误 的画6×”. (1)函数y=tanx-1有最小值无最大值.( (2)若函数=3c0s(2ax+)的周期为元,则a=1.( (3)可以用“五点法”作函数y=V2c0s(6+3)的简图.( (4)将y=sin(x+)的图象向左平移g个单位得到y=sinx的图 象(
导航

导航 课堂·重难突破 探究一作三角函数的图象 【例1】已知函数f)-V2sin(2ωx+)(w>0)的最小正周 期为π (1)求ω的值;(2)用“五点法”作出fx)的图象 分析:()利用了求0的值:2)按“五点法”的作图步骤进行
导航 课堂·重难突破 探究一 作三角函数的图象 【例1】 已知函数 (ω>0)的最小正周 期为π. (1)求ω的值;(2)用“五点法”作出f(x)的图象

导航 解:0器l 2)由()加,w)-V2sin(2x+星), 列表: π 3π 5π 7π 8 8 8 8 8 2.+ 元 3π 0 元 2元 4 2 2 fx) 0 V2 0 -V2 0
导航
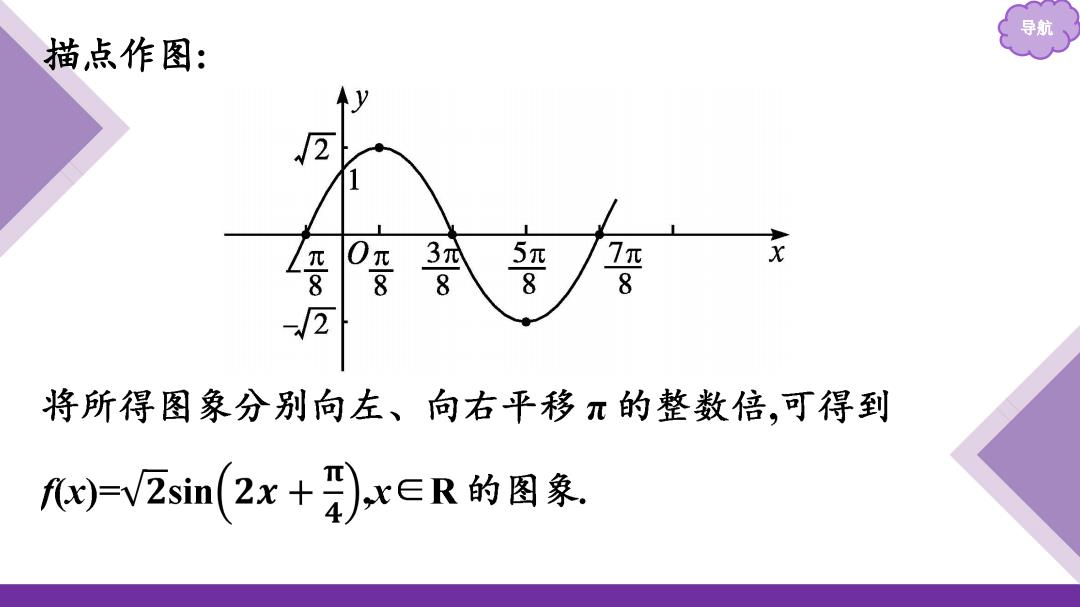
导航 描点作图: 3元 妥 x 8 将所得图象分别向左、向右平移π的整数倍,可得到 9-V2sin(2x+),x∈R的图象
导航 描点作图: