
全程设计 第九章 解三角形 9.2 正弦定理与余弦定理的应用理
第九章 解三角形 9.2 正弦定理与余弦定理的应用理
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解实际问题中有关的名称、术语 2.会建立实际应用题的三角形模型,并能运用正弦定理、余弦 定理解决问题 3.加强直观想象、逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.了解实际问题中有关的名称、术语. 2.会建立实际应用题的三角形模型,并能运用正弦定理、余弦 定理解决问题. 3.加强直观想象、逻辑推理和数学运算能力的培养

导 课前·基础认知 实际应用问题中有关的名称、术语 【问题思考】 1.甲身高2m,他站在离旗杆底部20m的M处,此时他看旗杆的 顶端A的仰角为60°,由此能否求得旗杆的高度? 提示:能如图, 旗杆高OA=OB+AB =2+20Xtan60° =2+20W3(m). W160 M
导航 课前·基础认知 实际应用问题中有关的名称、术语 【问题思考】 1.甲身高2 m,他站在离旗杆底部20 m的M处,此时他看旗杆的 顶端A的仰角为60° ,由此能否求得旗杆的高度? 提示:能.如图, 旗杆高OA=OB+AB =2+20×tan 60° =2+20 (m 𝟑 )
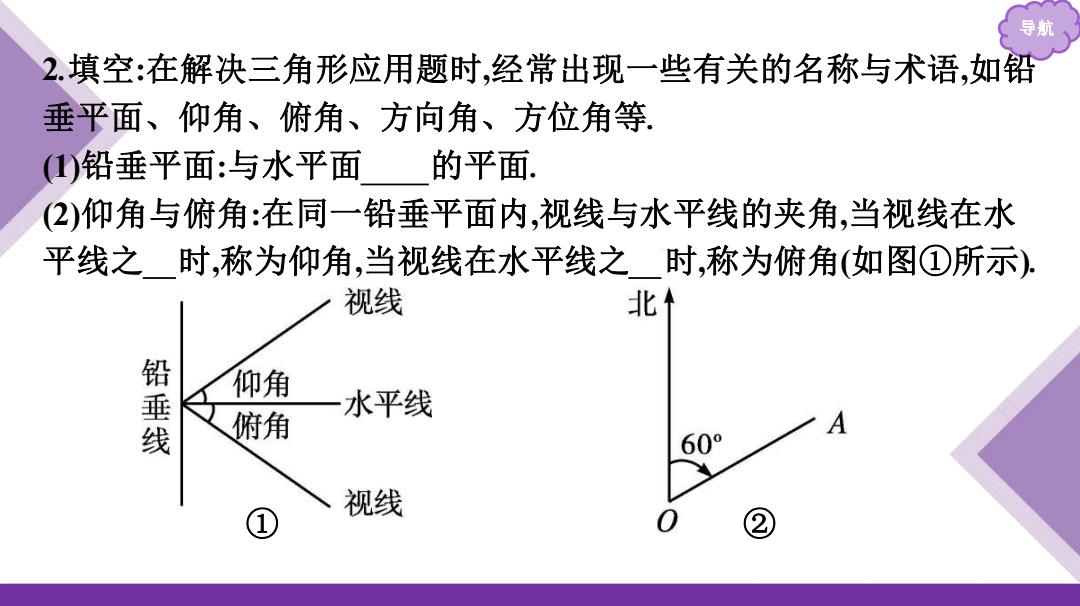
导航 2.填空:在解决三角形应用题时,经常出现一些有关的名称与术语,如铅 垂平面、仰角、俯角、方向角、方位角等 (1)铅垂平面:与水平面 的平面 (2)仰角与俯角:在同一铅垂平面内,视线与水平线的夹角,当视线在水 平线之时,称为仰角,当视线在水平线之时,称为俯角(如图①所示) 视线 北1 铅垂线 仰角 水平线 俯角 60° ① 视线 2
导航 2.填空:在解决三角形应用题时,经常出现一些有关的名称与术语,如铅 垂平面、仰角、俯角、方向角、方位角等. (1)铅垂平面:与水平面垂直的平面. (2)仰角与俯角:在同一铅垂平面内,视线与水平线的夹角,当视线在水 平线之上时,称为仰角,当视线在水平线之下时,称为俯角(如图①所示). ① ②

导航 3)方位角:从某点的指方向线起依 方向到目标方向 线间的水平角,如:图②表示的方位角是60°,或称北偏东60° (4)方向角:从指定 到 间的水平角,如南偏西 60°指以正南方向为始边,顺时针方向向西旋转60°
导航 (3)方位角:从某点的指北方向线起依顺时针方向到目标方向 线间的水平角,如:图②表示的方位角是60° ,或称北偏东60° . (4)方向角:从指定方向线到目标方向线间的水平角,如南偏西 60°指以正南方向为始边,顺时针方向向西旋转60°

导航 3.做一做:在300高的山顶上,测得山下有一塔的塔项与塔底 的俯角分别为30°,60°,则塔高为 m
导航 3.做一做:在300 m高的山顶上,测得山下有一塔的塔顶与塔底 的俯角分别为30°,60° ,则塔高为 m

导 解析:如图,在Rt△CDB中,CD=300m, ∠BCD=90°-60°=30°, 30° 020v3m .BC-5 A 在△ABC中,∠ABC=∠BCD=30°,∠ACB=60°30=30°. ∴.∠BAC=120°. B ..AB- C.sin30° in120° 三 2003×立-200(m 答案:200
导航 解析:如图,在Rt△CDB中,CD=300 m, ∠BCD=90°-60° =30° , ∴BC= 𝟑𝟎𝟎 𝐜𝐨𝐬𝟑𝟎° =200 𝟑(m). 在△ABC 中,∠ABC=∠BCD=30°,∠ACB=60°-30°=30°. ∴∠BAC=120°. ∴AB=𝑩𝑪·𝐬𝐢𝐧𝟑𝟎° 𝐬𝐢𝐧𝟏𝟐𝟎° = 𝟐𝟎𝟎 𝟑× 𝟏 𝟐 𝟑 𝟐 =200(m). 答案:200

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“X” (1)两个不可到达的点之间的距离无法求得.(×) (2)已知三角形的两角和一边,可以解三角形.(√) 3)视线与水平线的夹角就是仰角.(×) (4)从指北方向开始,逆时针转75°到目标位置,则方位角为 75°.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“ ”,错误 的画“×” . (1)两个不可到达的点之间的距离无法求得.( ) (2)已知三角形的两角和一边,可以解三角形.( ) (3)视线与水平线的夹角就是仰角.( ) (4)从指北方向开始,逆时针转75°到目标位置,则方位角为 75° .( ) × × ×
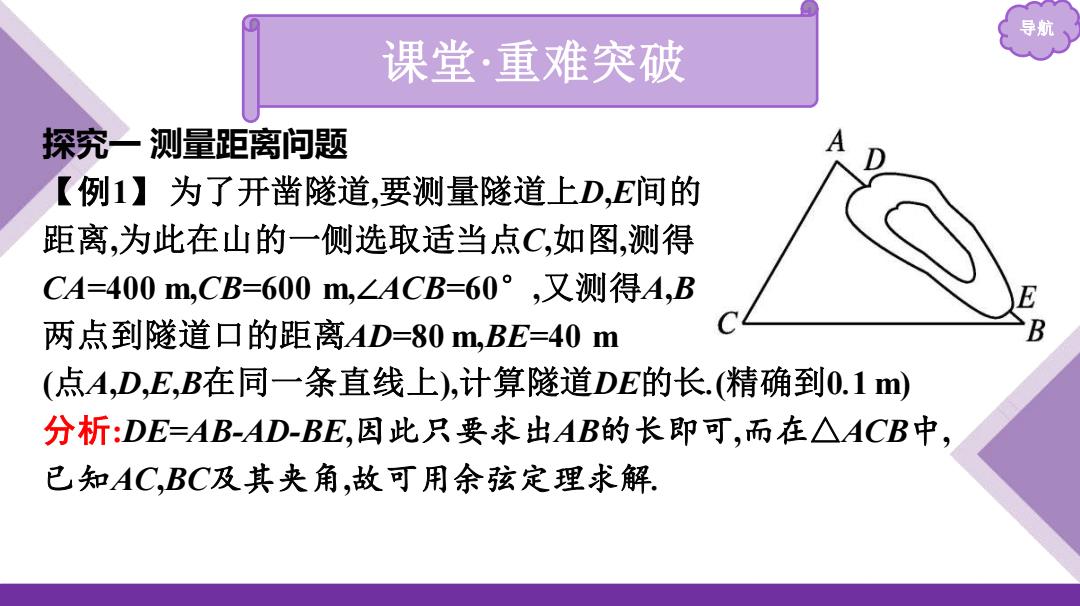
导航 课堂·重难突破 探究一测量距离问题 【例1】为了开凿隧道,要测量隧道上D,E间的 距离,为此在山的一侧选取适当点C,如图,测得 CA=400m,CB=600m,∠ACB=60°,又测得A,B 两点到隧道口的距离AD=80m,BE=40m (点A,D,E,B在同一条直线上),计算隧道DE的长.(精确到0.1m) 分析:DE=AB-AD-BE,因此只要求出AB的长即可,而在△ACB中, 已知AC,BC及其夹角,故可用余弦定理求解
导航 课堂·重难突破 探究一 测量距离问题 【例1】 为了开凿隧道,要测量隧道上D,E间的 距离,为此在山的一侧选取适当点C,如图,测得 CA=400 m,CB=600 m,∠ACB=60° ,又测得A,B 两点到隧道口的距离AD=80 m,BE=40 m (点A,D,E,B在同一条直线上),计算隧道DE的长.(精确到0.1 m) 分析:DE=AB-AD-BE,因此只要求出AB的长即可,而在△ACB中, 已知AC,BC及其夹角,故可用余弦定理求解