
全程设计 第十一章立体几何初步 11.3 空间中的平行关系 11.3.3 平面与平面平行
第十一章立体几何初步 11.3 空间中的平行关系 11.3.3 平面与平面平行
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.掌握空间中两个平面的位置关系. 2.掌握平面与平面平行的判定定理和性质定理,并能应用它们 解决问题 3.加强直观想象和逻辑推理能力的培养
导航 课标定位素养阐释 1.掌握空间中两个平面的位置关系. 2.掌握平面与平面平行的判定定理和性质定理,并能应用它们 解决问题. 3.加强直观想象和逻辑推理能力的培养

导航 课前·基础认知 一、平面与平面的位置关系 【问题思考】 1.平面a与平面的交点个数情况有哪些? 提示:无交点或无数个交点,两种情况
导航 课前·基础认知 一、平面与平面的位置关系 【问题思考】 1.平面α与平面β的交点个数情况有哪些? 提示:无交点或无数个交点,两种情况
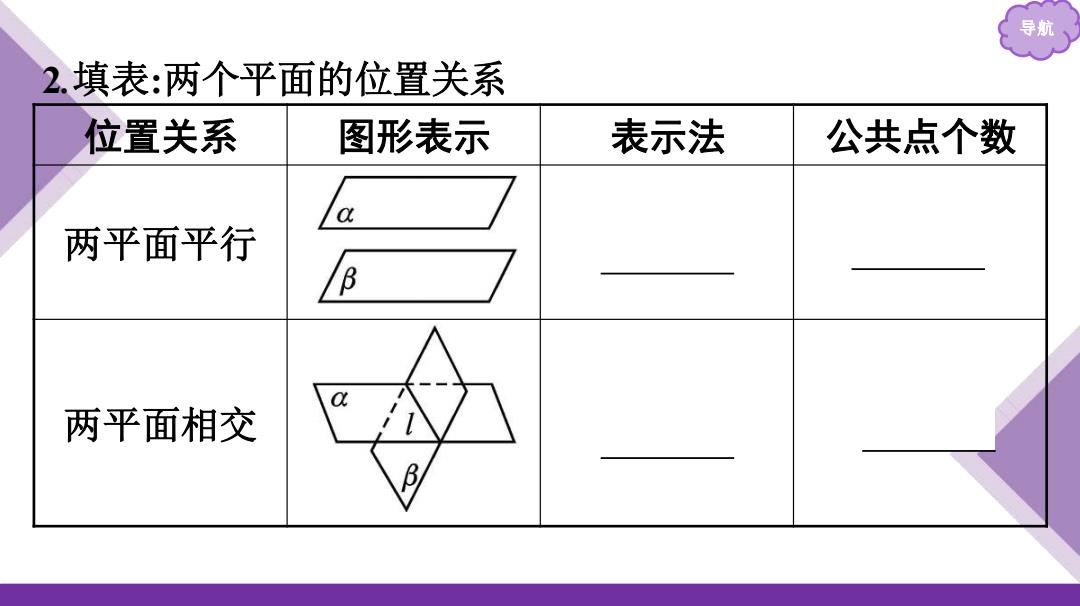
导航 2.填表:两个平面的位置关系 位置关系 图形表示 表示法 公共点个数 两平面平行 B 两平面相交
导航 2.填表:两个平面的位置关系 位置关系 图形表示 表示法 公共点个数 两平面平行 α∥β 0 两平面相交 α∩β=l 无数个

导航 3做一做:若平面a内的任何直线都平行于平面βB,则a与的位 置关系是 答案:alf
导航 3.做一做:若平面α内的任何直线都平行于平面β,则α与β的位 置关系是 . 答案:α∥β

导航 二、平面与平面平行的判定定理 【问题思考】 1.若平面a内有无数条直线都与平面B平行,则a与平行吗? 提示:不一定
导航 二、平面与平面平行的判定定理 【问题思考】 1.若平面α内有无数条直线都与平面β平行,则α与β平行吗? 提示:不一定

导月 2.填空:平面与平面平行的判定定理 ()文字语言:如果一个平面内有两条 直线分别平行于另 一个平面,那么这两个平面平行! (2)符号语言:如果1ca,mca,l∩呋o,llP,mIlB,那么alB. (3)图形表示:如图所示 m P 推论:如果一个平面内有两条 直线分别 平行于另一个平面内的 直线,那么这两 个平面平行
导航 2.填空:平面与平面平行的判定定理 (1)文字语言:如果一个平面内有两条相交直线分别平行于另 一个平面,那么这两个平面平行. (2)符号语言:如果l⊂α,m⊂α,l∩m≠⌀,l∥β,m∥β,那么α∥β. (3)图形表示:如图所示. 推论:如果一个平面内有两条相交直线分别 平行于另一个平面内的两条直线,那么这两 个平面平行
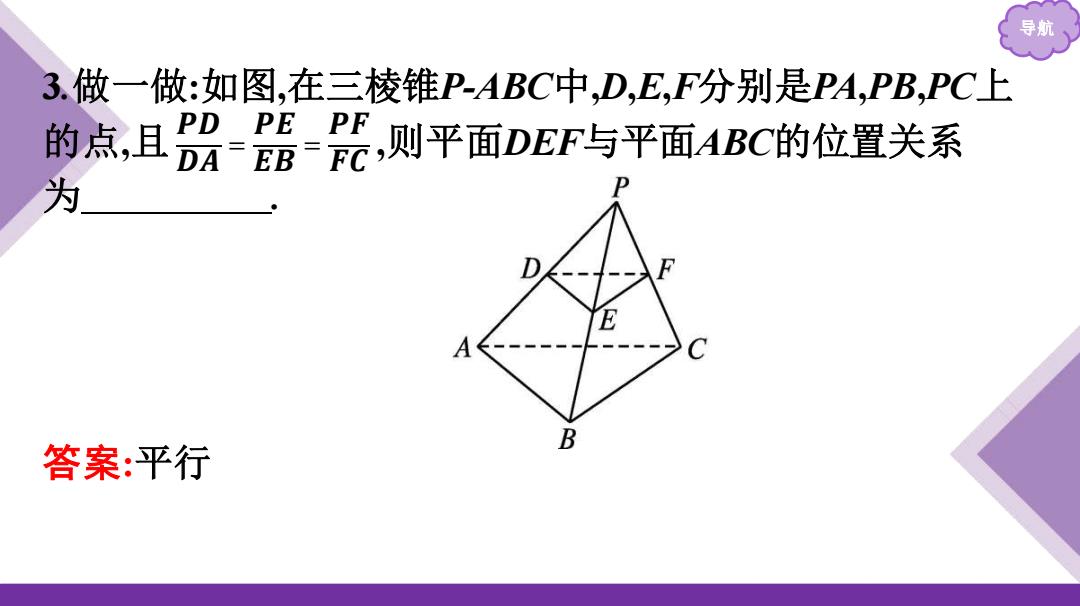
导航 3.做一做:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC上 的点,且册路,则平面DEF与平面ABC的位置关系 B 答案:平行
导航 3.做一做:如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC上 的点,且 ,则平面DEF与平面ABC的位置关系 为 . 答案:平行 𝑷𝑫 𝑫𝑨 = 𝑷𝑬 𝑬𝑩 = 𝑷𝑭 𝑭𝑪

导期 三、平面与平面平行的性质定理 【问题思考】 L.若平面al平面B,直线mca,直线ncf,则m与n的位置关系是 什么? 提示:平行或异面 2.已知平面αI平面B,直线lca,如何在平面B内作出一条直线, 使aI? 提示:过作一平面y,设y∩=a,则al
导航 三、平面与平面平行的性质定理 【问题思考】 1.若平面α∥平面β,直线m⊂α,直线n⊂β,则m与n的位置关系是 什么? 提示:平行或异面. 2.已知平面α∥平面β,直线l⊂α,如何在平面β内作出一条直线a, 使a∥l? 提示:过l作一平面γ,设γ∩β=a,则a∥l