
全程设计 第九章 解三角形 9.1 正弦定理与余弦定理 9.1.1 正弦定理 第1课时 ,正弦定理
第九章 解三角形 9.1 正弦定理与余弦定理 9.1.1 正弦定理 第1课时 正弦定理
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.理解正弦定理及其相关变式的推导过程 2.能应用正弦定理解三角形 3.加强逻辑推理与数学运算能力的培养
导航 课标定位素养阐释 1.理解正弦定理及其相关变式的推导过程. 2.能应用正弦定理解三角形. 3.加强逻辑推理与数学运算能力的培养

导航 课前·基础认知 正弦定理 【问题思考】 L在K△1BC中,若C-0,则有品=。者△1BC为斜 三角形式子=品B=成立吗? sinA sinB 提示:成立
导航 课前·基础认知 正弦定理 【问题思考】 提示:成立. 1.在 Rt△ABC 中,若 C=90°,则有 𝒂 𝐬𝐢𝐧𝑨 = 𝒃 𝐬𝐢𝐧𝑩 =c= 𝒄 𝐬𝐢𝐧𝑪 ;若△ABC 为斜 三角形,式子 𝒂 𝐬𝐢𝐧𝑨 = 𝒃 𝐬𝐢𝐧𝑩 = 𝒄 𝐬𝐢𝐧𝑪 成立吗?
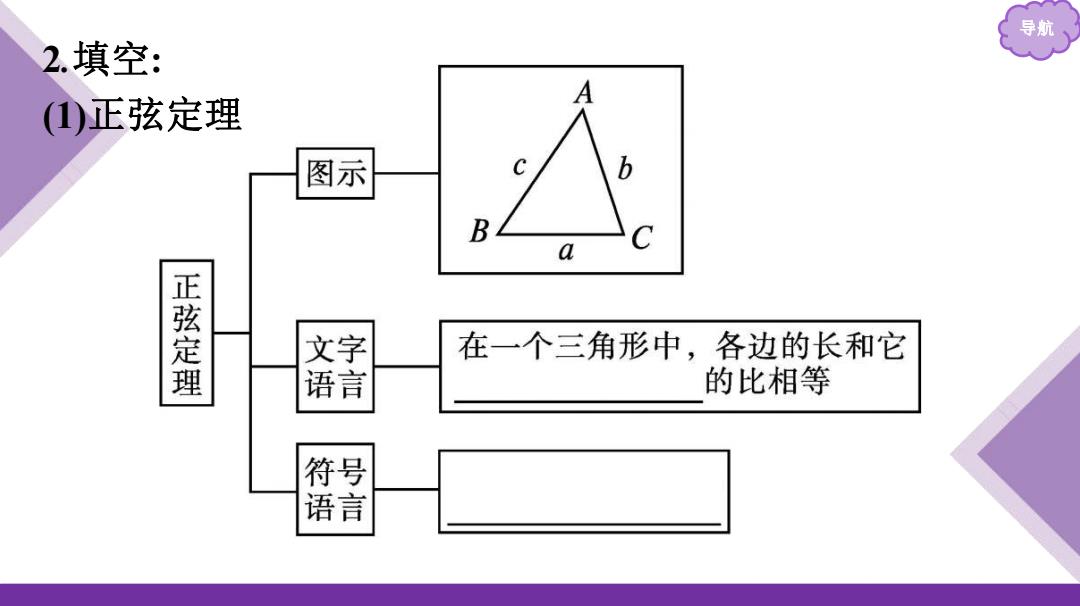
导航 2.填空: ()正弦定理 图示 B C a 正弦定理 文字 在一个三角形中,各边的长和它 语言 的比相等 符号 语言
导航 2 .填空 : (1)正弦定理

导航 2)面积公式 (3)解三角形 三角形的3个角与3条边都称为三角形的 ,已知三角形的 若干元素求其他元素一般称为解三角形 3.在一个三角形中,若只知道三个角,能解这个三角形吗? 提示:不能
导航 (2)面积公式 (3)解三角形 三角形的3个角与3条边都称为三角形的元素,已知三角形的 若干元素求其他元素一般称为解三角形. 3.在一个三角形中,若只知道三个角,能解这个三角形吗? 提示:不能. S= 𝟏 𝟐 𝒂𝒃𝐬𝐢𝐧 𝑪 = 𝟏 𝟐 𝒂𝒄𝐬𝐢𝐧 𝑩 = 𝟏 𝟐 𝒃𝒄𝐬𝐢𝐧 𝑨

导航 4.做一做: (①在△4BC中,若A=60°,B=45°,BC=3V2,则AC=一 (2)在△ABC中,若3,b=V3,A-,则C=
导航 4 .做一做: (1) 在 △ABC 中,若 A=60°,B=45°,BC= 3 𝟐,则 AC= . (2) 在 △ABC 中,若 a=3,b= 𝟑,A=𝛑𝟑,则 C=

导航 解析:(1)由正弦定理得 3V2 AC sin60° sin450? 所以AC-32D2V3 (2)由正弦定理得3 3 sin 3 又因为>b,所以A>B, 则B6C-n-(G+君)= 答案:(1)23(2
导航 答案:(1)2 𝟑 (2)𝛑 𝟐 解析:(1)由正弦定理得 𝟑 𝟐 𝐬𝐢𝐧𝟔𝟎° = 𝑨𝑪 𝐬𝐢𝐧𝟒𝟓° , 所以 AC=𝟑 𝟐·𝐬𝐢𝐧𝟒𝟓° 𝐬𝐢𝐧𝟔𝟎° =2 𝟑. (2)由正弦定理得 𝟑 𝐬𝐢𝐧 𝛑 𝟑 = 𝟑 𝐬𝐢𝐧𝑩 ,sin B=𝟏 𝟐 . 又因为 a>b,所以 A>B, 则 B=𝛑 𝟔 ,C=π- 𝛑 𝟑 + 𝛑 𝟔 = 𝛑 𝟐

【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“√”,错误 的画“X” (1)正弦定理适用于任何三角形.(√) (2)在△ABC中,等式bsin A=asin B定成立.(√) (3)在△ABC中,a:b:c=sinA:sinB:sinC.(V) (4)在△ABC中,若sinA=sinC,则△ABC必为等腰三角形.(√) (5)SAABC-absin C=bcsin A.(X
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号里画“ ”,错误 的画“×” . (1)正弦定理适用于任何三角形.( ) (2)在△ABC中,等式bsin A=asin B一定成立.( ) (3)在△ABC中,a∶b∶c=sin A∶sin B∶sin C.( ) (4)在△ABC中,若sin A=sin C,则△ABC必为等腰三角形.( ) (5)S△ABC=absin C=bcsin A.( ) ×

导航 课堂·重难突破 探究一已知三角形两角和任一边解三角形 【例1】在△ABC中,已知A=45°,B=30°,=2,解此三角形 分析:利用A+B+C=180°及正弦定理求解
导航 课堂·重难突破 探究一 已知三角形两角和任一边解三角形 【例1】在△ABC中,已知A=45° ,B=30° ,a=2,解此三角形. 分析:利用A+B+C=180°及正弦定理求解