
全程设计 第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.2 向量的加法
第六章 平面向量初步 6.1 平面向量及其线性运算 6.1.2 向量的加法

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 三角形法则 【问题思考】 1.早上,小明去学校,从家(记为A)去了正北方向的学校(记为B) 中午放学,他又从学校去了学校正东方向的外婆家(记作C).小 明从A到C的位移与从A到B、从B到C的位移有关系吗? 提示:有
导航 课前·基础认知 一、三角形法则 【问题思考】 1.早上,小明去学校,从家(记为A)去了正北方向的学校(记为B). 中午放学,他又从学校去了学校正东方向的外婆家(记作C).小 明从A到C的位移与从A到B、从B到C的位移有关系吗? 提示:有

2.填空:(1)三角形法则 般地,平面上任意给定两个向量a,b,在该平面内任取一点A,作 AB=a,BC=b,作出向量AC,则向量AC称为向量a与b的和(也称 AC为向量a与b的和向量).向量a与b的和向量记作,因此 AB+BC=AC. 上述求两个向量和的作图方法也常称为向量加法的三角形法 则. (2)对于任意向量a,有a0=+_=一· (3) ≤la+bl≤ a+0
导航 2.填空:(1)三角形法则 一般地,平面上任意给定两个向量 a,b,在该平面内任取一点 A,作 𝑨 𝑩 =a,𝑩 𝑪 =b,作出向量𝑨 𝑪 ,则向量𝑨 𝑪 称为向量 a 与 b 的和(也称 𝑨 𝑪 为向量 a 与 b 的和向量).向量 a 与 b 的和向量记作 a+b,因此 𝑨 𝑩 + 𝑩 𝑪 = 𝑨 𝑪 . 上述求两个向量和的作图方法也常称为向量加法的三角形法 则. (2)对于任意向量a,有a+0=0+ a = a . (3) ||a|-|b|| ≤|a+b|≤ |a|+|b |

导航 3.两个向量的和一定是向量吗? 提示:是 4.做一做:若1a=1,b=5,则a+b的取值范围是 答案[4,6
导航 3.两个向量的和一定是向量吗? 提示:是. 4.做一做:若|a|=1,|b|=5,则|a+b|的取值范围是 . 答案:[4,6]

导期 二、向量加法的平行四边形法则 【问题思考】 1.在重力2N的作用下,物体M做自由落体运动,现有一水平方 向微风以0.2N的力作用于M上,物体M下落的轨迹有变化吗? 物体M受的力是2.2N吗? 提示:有变化;不是
导航 二、向量加法的平行四边形法则 【问题思考】 1.在重力2 N的作用下,物体M做自由落体运动,现有一水平方 向微风以0.2 N的力作用于M上,物体M下落的轨迹有变化吗? 物体M受的力是2.2 N吗? 提示:有变化;不是
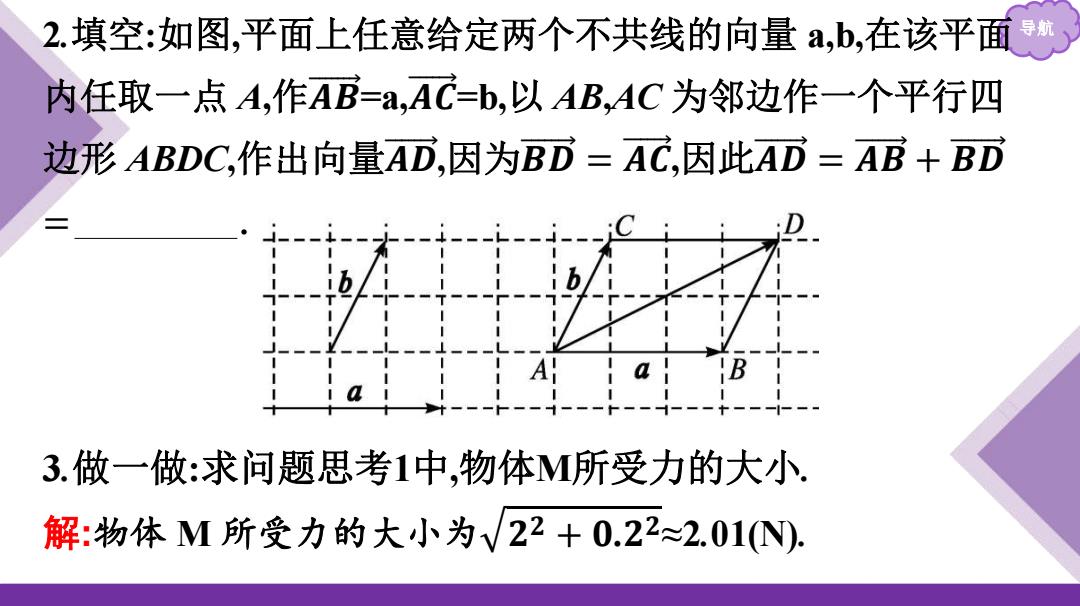
2.填空:如图,平面上任意给定两个不共线的向量a,b,在该平面导航 内任取一点A,作AB=a,AC=b,以AB,AC为邻边作一个平行四 边形ABDC,作出向量AD,因为BD=AC,因此AD=AB+BD 3.做一做:求问题思考1中,物体M所受力的大小 解:物体M所受力的大小为V22+0.22≈2.01N)
导航 2.填空:如图,平面上任意给定两个不共线的向量 a,b,在该平面 内任取一点 A,作𝑨 𝑩 =a,𝑨 𝑪 =b,以 AB,AC 为邻边作一个平行四 边形 ABDC,作出向量𝑨 𝑫 ,因为𝑩 𝑫 = 𝑨 𝑪 ,因此𝑨 𝑫 = 𝑨 𝑩 + 𝑩 𝑫 = 𝑨 𝑩 + 𝑨 𝑪 . 3.做一做:求问题思考1中,物体M所受力的大小. 解:物体 M 所受力的大小为 𝟐 𝟐 + 𝟎.𝟐 𝟐 ≈2.01(N)

三、多个向量相加 导期 【问题思考】 1,不共线的三个力同时作用于物体M上,如何求它们的合力? 提示:可以两次应用三角形(或平行四边形)法则. 2.填空:(1)求有限个向量的和时,只需将这些向量依次 相 接,那么以第一个向量的 为始点,最后一个向量的 为 终点的向量,就是这些向量的和 (2)向量加法的运算律 交换律 a+b= 结合律 (a+b)+c=a+
三、多个向量相加 导航 【问题思考】 1.不共线的三个力同时作用于物体M上,如何求它们的合力? 提示:可以两次应用三角形(或平行四边形)法则. 2.填空:(1)求有限个向量的和时,只需将这些向量依次首尾相 接,那么以第一个向量的始点为始点,最后一个向量的终点为 终点的向量,就是这些向量的和. (2)向量加法的运算律 交换律 a+b=b+a 结合律 (a+b)+c=a+(b+c)

导航、 3.做一做: 化简:AB+CD+OA+BC= 答案:0D
导航 3 .做一做 : 化简:𝑨 𝑩 + 𝑪 𝑫 + 𝑶 𝑨 + 𝑩 𝑪 = . 答案:𝑶 𝑫

导航 课堂·重难突破 探究一求向量模的最值 【例1】己知la=10,b=2,求a+b的最大值和最小值. 解:.la-Hbll≤la+b≤la+bl, ∴.当a与b的方向相同时,a+b取得最大值10+2=12; 当a与b的方向相反时,a+b取得最小值10-2=8. 故|a+b的最大值为12,最小值为8
导航 课堂·重难突破 探究一 求向量模的最值 【例1】已知|a|=10,|b|=2,求|a+b|的最大值和最小值. 解:∵||a|-|b||≤|a+b|≤|a|+|b|, ∴当a与b的方向相同时,|a+b|取得最大值10+2=12; 当a与b的方向相反时,|a+b|取得最小值|10-2|=8. 故|a+b|的最大值为12,最小值为8