
全程设计 第四章> 指数函数、对数函数与幂函数 4.2对数与对数函数 4.2.2 对数运算法贝则
第四章 指数函数、对数函数与幂函数 4.2 对数与对数函数 4.2.2 对数运算法则

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 一、对数的运算性质 【问题思考】 1.我们知道,aM+w=aM·aN,那么log(M)与log,M,logN有什么 关系呢? 提示:log(MW=log MHog N(a>0,1,M0,N0)
导航 课前·基础认知 一、对数的运算性质 【问题思考】 1.我们知道,a M+N=a M·a N ,那么loga (M·N)与logaM,logaN有什么 关系呢? 提示:loga (M·N)=logaM+logaN(a>0,a≠1,M>0,N>0)

2.填空:对数运算具有运算法则 导航 log (MN)= log Mo= M 10g"N 其中,>0且味1,M>0,W>0,a∈R 3.做一做: 求值:(1)g2+lg5= (2)log2V4= 答案:(1) 1(2号
导航 2 .填空 :对数运算具有运算法则 log a (MN)= log aM+log aN , log aMα= αlog aM , log a 𝑴𝑵 = log aM-log aN . 其中 ,a> 0 且 a≠1,M>0,N>0, α ∈ R. 3 .做一做 : 求值:(1)lg 2 +lg 5 = ; (2)log 2 𝟒𝟑 = . 答案:(1)1 (2) 𝟐𝟑

导期 二、换底公式 【问题思考】 1.对数1og32能否用1g2和lg3表示?能否用1n2和ln3表示?能否 用1og2和log3表示? 提示:l0g2oee =g2 In2 loga3 1g3 In3" 2.填空:一般地,我们有log,b18cb logca 其中>0且呋1,b>0,c>0且c≠1,这一结果通常被称为
导航 二、换底公式 【问题思考】 1.对数log32能否用lg 2和lg 3表示?能否用ln 2和ln 3表示?能否 用loga2和loga3表示? 提示:log32= 𝐥𝐨𝐠𝒂 𝟐 𝐥𝐨𝐠𝒂 𝟑 = 𝐥𝐠𝟐 𝐥𝐠𝟑 = 𝐥𝐧𝟐 𝐥𝐧𝟑 . 2.填空:一般地,我们有 logab=𝐥𝐨𝐠𝒄 𝒃 𝐥𝐨𝐠𝒄 𝒂 其中a>0且a≠1,b>0,c>0且c≠1,这一结果通常被称为换底公式
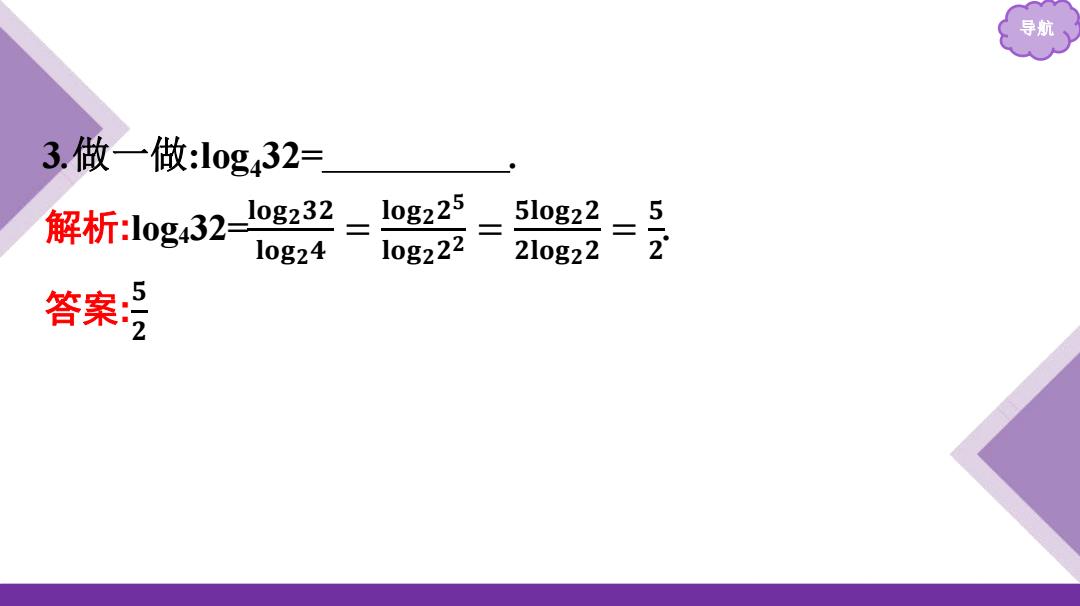
导航 3.做一做:l0g432= 解析:log32-0e23 10g225 510g22 10g24 10g222 210g22 5-2 答案
导航 解析:log 432 =𝐥𝐨 𝐠 𝟐 𝟑 𝟐 𝐥𝐨𝐠𝟐𝟒 = 𝐥𝐨 𝐠 𝟐 𝟐 𝟓 𝐥𝐨𝐠𝟐𝟐𝟐 = 𝟓𝐥𝐨 𝐠 𝟐 𝟐 𝟐𝐥𝐨 𝐠 𝟐 𝟐 = 𝟓𝟐. 3 .做一做:log 432 = . 答案:𝟓𝟐

导航 课堂·重难突破 探究一对数运算性质的应用 【例1】求下列各式的值: (lg14-2lg3+lg7-lg18; 21g2+1g3 22+lg0.36+26e 3og4g25g4+792, (4)2log2-logHog8-52lgs3
导航 课堂 ·重难突破 探究 一 对数运算性质的应用 【例 1 】求下列各式的值 : (1)lg 14-2lg 𝟕𝟑 +lg 7-lg 18; (2) 𝟐𝐥𝐠 𝟐 +𝐥𝐠 𝟑 𝟐 +𝐥𝐠 𝟎.𝟑 𝟔 + 𝟐𝐥𝐠 𝟐; (3)log 3 𝟐 𝟕 𝟒 𝟑 +lg 25 +lg 4 + 𝟕𝒍𝒐 𝒈 𝟕 𝟐; (4)2log 3 2-log 3 𝟑 𝟐𝟗 +log 3 8-𝟓 𝟐𝒍𝒐 𝒈 𝟓 𝟑

分析:若对数的底数相同,则直接利用对数的运算性质求解注 意性质的正用和逆用 解(1)原式=g(2×7)-2g7-lg3)+lg7-lg(32×2) =lg2+lg7-2lg7+2g3+lg7-2g3-lg2=0. (2)原式= 21g2+lg3 21g2+1g3 21g2+1g3 1 2+lg36-2+2lg22(lg2+lg3)+2lg2 41g2+21g3 3 3)原式=1og+lg(25x4+2=10g3g102+2-+2+2-号 34 (4)原式=2l0g32-(log325-l0g39)+3l0g32-510g532 =2l0g32-5l0g32+2l0g33+310g32-9=2-9=-7
导航 (2)原式= 𝟐𝒍𝒈𝟐+𝒍𝒈𝟑 𝟐+𝒍𝒈𝟑𝟔-𝟐+𝟐𝒍𝒈𝟐 = 𝟐𝒍𝒈𝟐+𝒍𝒈𝟑 𝟐(𝒍𝒈𝟐+𝒍𝒈𝟑)+𝟐𝒍𝒈𝟐 = 𝟐𝒍𝒈𝟐+𝒍𝒈𝟑 𝟒𝒍𝒈𝟐+𝟐𝒍𝒈𝟑 = 𝟏 𝟐 . (3)原式=log3 𝟑 𝟑 𝟒 𝟑 +lg(25×4)+2=log3𝟑 - 𝟏 𝟒+lg 102 +2=- 𝟏 𝟒 +2+2= 𝟏𝟓 𝟒 . (4)原式=2log32-(log32 5 -log39)+3log32-𝟓 𝒍𝒐𝒈𝟓 𝟑 𝟐 =2log32-5log32+2log33+3log32-9=2-9=-7. 分析:若对数的底数相同,则直接利用对数的运算性质求解.注 意性质的正用和逆用. 解:(1)原式=lg(2×7)-2(lg 7-lg 3)+lg 7-lg(32×2) =lg 2+lg 7-2lg 7+2lg 3+lg 7-2lg 3-lg 2=0

导 反思感悟1.运用对数的运算性质求值时注意性质的正用和逆 用. 2.对于复杂的运算式,可先化简再计算;化简问题的常用方 法:1)“拆”:将积(商)的对数拆成两对数之和(差)52)“收”:将同 底对数的和(差)收成积(商)的对数
导航 反思感悟 1.运用对数的运算性质求值时注意性质的正用和逆 用. 2.对于复杂的运算式,可先化简再计算;化简问题的常用方 法:(1)“拆”:将积(商)的对数拆成两对数之和(差);(2)“收”:将同 底对数的和(差)收成积(商)的对数

【变式训练1】求下列各式的值, 导航 (①32-1o82; (log-35-2logsHogs7-logs1.8 (3)g5)2+2lg2-(g2)2. 解:(1)32-1ogg2=32 9 9 F387=N52a厚=5F 9-4 9 (2)原式=logs5×7)-2(l0g57-l0gs3)+H0gs7-l0g =l0gs5+l0gs7-2l0gs7+2l0gs3+l0g57-2l0g53+1=2. (③)原式=((g5+g2)(g5-lg2)+2g2=g10-lg+g4 =lg(×4)=g10=1
【变式训练 导航 1】求下列各式的值. (1) 𝟑 𝟐-𝐥𝐨 𝐠 𝟑 𝟐; (2)log 535-2log 5 𝟕𝟑 +log 5 7-log 51.8; (3)(lg 5) 2 +2lg 2-(lg 2) 2. 解:(1)𝟑𝟐-𝐥𝐨𝐠 𝟑𝟐 = 𝟑𝟐 𝟑𝐥𝐨𝐠 𝟑 𝟐 = 𝟗 ( 𝟑)𝟐𝐥𝐨 𝐠 𝟑 𝟐 = 𝟗 ( 𝟑)𝐥𝐨 𝐠 𝟑 𝟒 = 𝟗𝟒. (2)原式 =log 5(5 ×7)-2(log 5 7-log 53) +log 5 7-log 5 𝟗𝟓 =log 5 5 +log 5 7-2log 5 7 +2log 5 3 +log 5 7-2log 5 3 +1= 2. (3)原式 =(lg 5 +lg 2)(lg 5-lg 2) +2lg 2 =lg 10·lg 𝟓𝟐 +lg 4 =lg 𝟓𝟐 × 𝟒 =lg 10 =1