
全程设计 8.1.1 向量数量积的概念
8.1.1 向量数量积的概念

导航 课标定位 素养阐释 1.理解平面向量数量积的含义及其物理意义, 2.体会平面向量的数量积与向量投影的关系. 3.掌握数量积的运算性质,加强直观想象、数学运算能力的培 养
导航 课标定位 素养阐释 1.理解平面向量数量积的含义及其物理意义. 2.体会平面向量的数量积与向量投影的关系. 3.掌握数量积的运算性质,加强直观想象、数学运算能力的培 养
课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 课前·基础认知 两个向量的夹角 【问题思考】 1.若F和F,是作用于同一点的两个力,则此两个力的张角最大 是多少?最小是多少? 提示:元,0
导航 课前·基础认知 一、两个向量的夹角 【问题思考】 1.若F1和F2是作用于同一点的两个力,则此两个力的张角最大 是多少?最小是多少? 提示:π,0

2.填空:(1)给定两个非零向量a,b,在平面内任选一点O,作 0A=a,0B=b,则称l 内的∠AOB为向量a与向量b的夹角, 记作 (2)若a,b是两个非零向量则的范围是 ;与2时,称向量a与向量b垂直,记作 规定零向量 与 向量垂直 3.做一做:在Rt△ABC中,∠C=90°,AC=BC,则 ;与BC垂直的向量有 答案:135° Ac,CA
导航 2.填空:(1)给定两个非零向量 a,b,在平面内任选一点 O,作 𝑶 𝑨 =a,𝑶 𝑩 =b,则称[0,π]内的∠AOB 为向量 a 与向量 b 的夹角, 记作. (2)若 a,b 是两个非零向量,则的范围是[0,π];与 是相等的. (3)当= 𝛑 𝟐 时,称向量 a 与向量 b 垂直,记作 a⊥b.规定零向量 与任意向量垂直. 3.做一做:在 Rt△ABC 中,∠C=90°,AC=BC,则 = ;与𝑩 𝑪 垂直的向量有 . 答案:135° 𝑨 𝑪 ,𝑪 𝑨

导航 二、向量数量积的定义 【问题思考】 1.作用在物体上的力F所做功的大小,取决于哪些因素? 提示:力F的大小,物体在力F作用下位移的大小及F与位移夹 角的余弦值
导航 二、向量数量积的定义 【问题思考】 1.作用在物体上的力F所做功的大小,取决于哪些因素? 提示:力F的大小,物体在力F作用下位移的大小及F与位移夹 角的余弦值

导期 2.填空: (1)向量数量积的定义:一般地,当a与b都是非零向量时,称 为向量a与b的数量积(也称为内积),记作ab,即 a.b= :两个非零向量a与b的数量积是一个: (2)向量数量积的性质: ①labl_lalb; ②a2=a'a=,即a=Vaa; ③a⊥b台; ④c0s- a-b ab
导航 2.填空: (1)向量数量积的定义:一般地,当a与b都是非零向量时,称 |a||b|cos为向量a与b的数量积(也称为内积),记作a·b,即 a·b=|a||b|cos.两个非零向量a与b的数量积是一个实数. (2)向量数量积的性质: ①|a·b|≤|a||b|; ②a 2 =a·a=|a| 2 ,即|a|= 𝒂·𝒂; ③a⊥b⇔a·b=0; ④cos= 𝒂·𝒃 |𝒂||𝒃|

导航 3.两非零向量a,b的数量积一定是一个非负数吗? 提示:不一定 4.做一做:在边长为1的正方形ABCD中,AB.BC= AD.CA= :DA.BC= 答案:01-1
导航 3.两非零向量a,b的数量积一定是一个非负数吗? 提示:不一定. 4.做一做:在边长为 1 的正方形 ABCD 中,𝑨 𝑩 ·𝑩 𝑪 = ; 𝑨 𝑫 ·𝑪 𝑨 = ;𝑫 𝑨 ·𝑩 𝑪 = . 答案:0 -1 -1
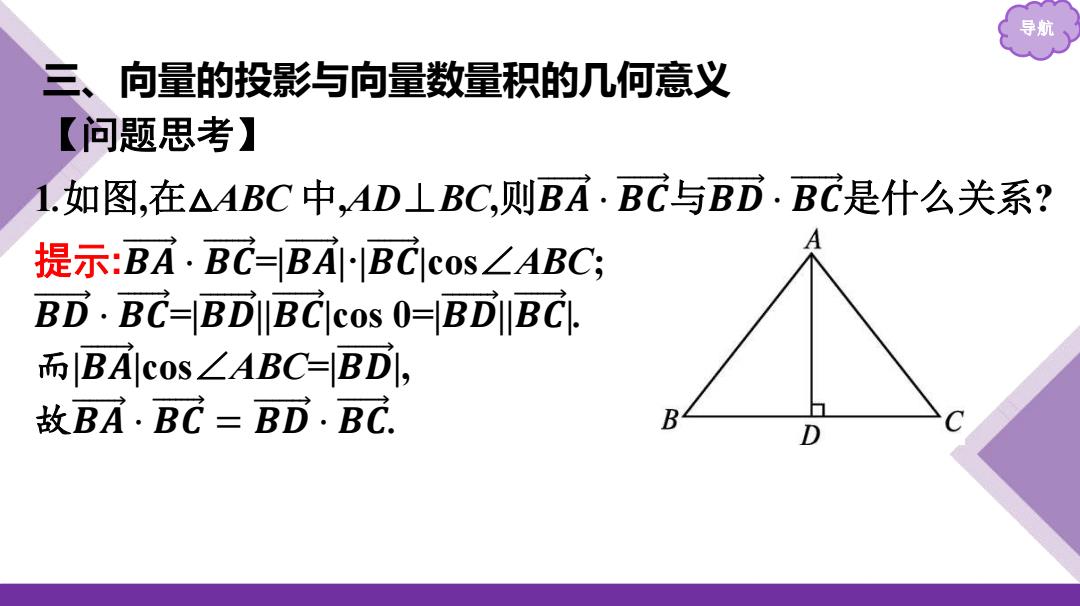
导 三、向量的投影与向量数量积的几何意义 【问题思考】 1.如图,在△ABC中,AD⊥BC,则BA·BC与BD.BC是什么关系? 提示:BA·BC=BABCcos∠ABC; BD.BC-BDBCcos 0=BDBC. 而BAcos.∠ABC=BD, 故BA.BC=BD.BC B
导航 三、向量的投影与向量数量积的几何意义 【问题思考】 1.如图,在△ABC 中,AD⊥BC,则𝑩 𝑨 ·𝑩 𝑪 与𝑩 𝑫 ·𝑩 𝑪 是什么关系? 提示:𝑩 𝑨 ·𝑩 𝑪 =|𝑩 𝑨 |·|𝑩 𝑪 |cos∠ABC; 𝑩 𝑫 ·𝑩 𝑪 =|𝑩 𝑫 ||𝑩 𝑪 |cos 0=|𝑩 𝑫 ||𝑩 𝑪 |. 而|𝑩 𝑨 |cos∠ABC=|𝑩 𝑫 |, 故𝑩 𝑨 ·𝑩 𝑪 = 𝑩 𝑫 ·𝑩 𝑪

2.填空:(1)设非零向量AB=A,过点A,B分别作直线1的垂线,垂 足分别为A',B',则称向量A'B为向量a在直线1上的投影向量 或投影 (2)给定平面上的一个非零向量b,设b所在的直线为l,则a在直 线上的投影称为a在向量上的投影 3)一般地,如果a,b都是非零向量,则称 为向量a在 向量b上的投影的数量.投影的数量与投影的长度有关,但投 影的数量既可能是非负数,也可能是负数
导航 2.填空:(1)设非零向量𝑨 𝑩 =a,过点 A,B 分别作直线 l 的垂线,垂 足分别为 A',B',则称向量𝑨'𝑩' 为向量 a 在直线 l上的投影向量 或投影. (2)给定平面上的一个非零向量b,设b所在的直线为l,则a在直 线l上的投影称为a在向量b 上的投影. (3)一般地,如果a,b都是非零向量,则称|a|cos为向量a在 向量b上的投影的数量.投影的数量与投影的长度有关,但投 影的数量既可能是非负数,也可能是负数