
全程设计 3.3 函数的应用(一)
3.3 函数的应用(一)
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1通过运用函数的有关知识解决实际生活中的问题,加深对函 数概念的理解 2.会应用一次函数、二次函数模型解决实际问题 3.体会数学知识来源于生活,又服务于生活:
导航 课标定位素养阐释 1.通过运用函数的有关知识解决实际生活中的问题,加深对函 数概念的理解. 2.会应用一次函数、二次函数模型解决实际问题. 3.体会数学知识来源于生活,又服务于生活
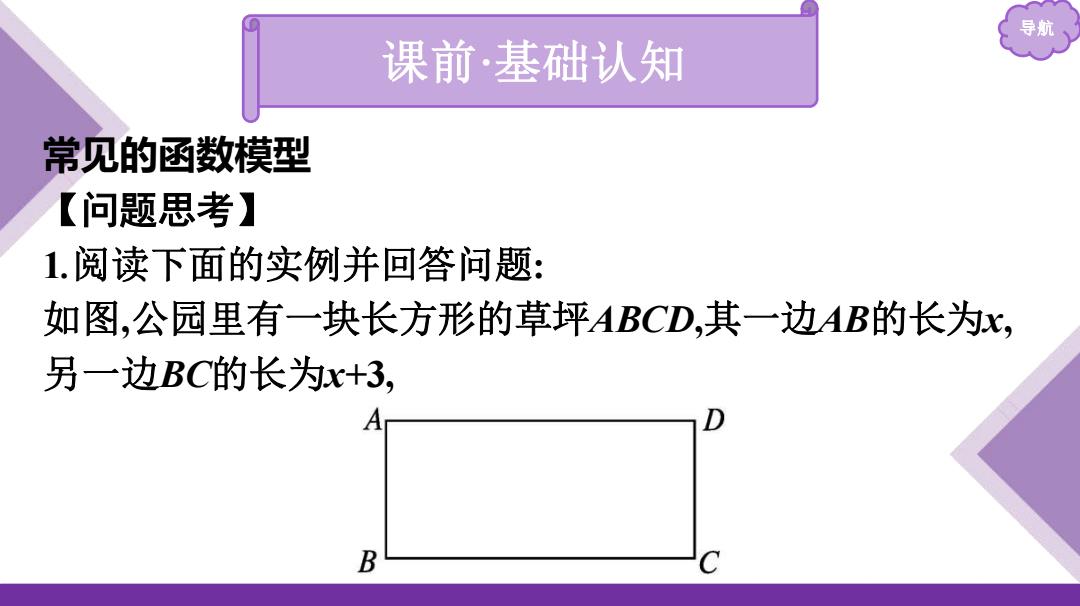
导航 课前·基础认知 常见的函数模型 【问题思考】 1.阅读下面的实例并回答问题: 如图,公园里有一块长方形的草坪ABCD,其一边AB的长为x, 另一边BC的长为x+3, B C
导航 课前·基础认知 常见的函数模型 【问题思考】 1.阅读下面的实例并回答问题: 如图,公园里有一块长方形的草坪ABCD,其一边AB的长为x, 另一边BC的长为x+3

导航 1)求长方形ABCD的周长fx)和面积g(x) 提示:fx)=2x+2(x+3)=4x+6(x>0), g(x)=x(x+3)=x2+3x>0). (2)函数fx)和gx)是一次函数还是二次函数? 提示fx)是一次函数gx)是二次函数. (3)用函数的知识解决实际问题,需要用到一些函数模型,常见 的函数模型有哪些? 提示:一次函数、二次函数、反比例函数等
导航 (1)求长方形ABCD的周长f(x)和面积g(x). 提示:f(x)=2x+2(x+3)=4x+6(x>0), g(x)=x(x+3)=x2+3x(x>0). (2)函数f(x)和g(x)是一次函数还是二次函数? 提示:f(x)是一次函数,g(x)是二次函数. (3)用函数的知识解决实际问题,需要用到一些函数模型,常见 的函数模型有哪些? 提示:一次函数、二次函数、反比例函数等

2.填空: 导航 三类常见的函数模型 名称 解析式 条件 次函数模型 v-ktb 0 函数模型 X 般式y=x2+bx+c 二次函数模型 顶点式=(x+)子+ 4ac-b2 呋0 4a
导航 2 .填空 : 三类常见的函数模型 名 称 解析式 条 件 一次函数模型 y=kx+b k≠ 0 反比例 函数模型 y= 𝐤𝐱 +b k≠ 0 二次函数模型 一般式:y=ax 2 +bx+c 顶点式:y=a 𝐱 + 𝐛𝟐𝐚 𝟐 + 𝟒 𝐚𝐜-𝐛 𝟐 𝟒 𝐚 a ≠ 0

导 3.做一做: ()随着海拔的升高,大气的压强下降,空气中的含氧量也随之 下降,且含氧量y(单位:g/m3)与大气压x(单位:kPa)成正比例函 数关系.当=36kPa时y=108g/m3,则y与x的函数解析式为 AJy=3x(c≥0) B.y=3x CJ字≥0)Dy子x
导航 3.做一做: (1)随着海拔的升高,大气的压强下降,空气中的含氧量也随之 下降,且含氧量y(单位:g/m3 )与大气压x(单位:kPa)成正比例函 数关系.当x=36 kPa时,y=108 g/m3 ,则y与x的函数解析式为 ( ) A.y=3x(x≥0) B.y=3x C.y= 𝟏 𝟑 x(x≥0) D.y= 𝟏 𝟑 x

导 (2)已知某化工厂在一月份生产某种产品200t,三月份生产yt, 则y与月平均增长率x之间的关系是() A.v=200x B.Jy=200x2 CJy=200(1+x) DJy=200(1+x)2
导航 (2)已知某化工厂在一月份生产某种产品200 t,三月份生产y t, 则y与月平均增长率x之间的关系是( ) A.y=200x B.y=200x 2 C.y=200(1+x) D.y=200(1+x) 2

导航 解析:1)由题意,设y=x(0),将(36,108)代入解析式可得k=3, 即y=3x,考虑到含氧量y不可能为负,可知x≥0. (2)一月份生产200t, 二月份生产200x+200=200(x+1)t, 三月份生产200(c+1)x+200(x+1)=200(x+1)x+1)=200(x+1)2t, 即y=200(c+1)2. 答案:1)A(2)D
导航 解析:(1)由题意,设y=kx(k≠0),将(36,108)代入解析式可得k=3, 即y=3x,考虑到含氧量y不可能为负,可知x≥0. (2)一月份生产200 t, 二月份生产200x+200=200(x+1)t, 三月份生产200(x+1)x+200(x+1)=200(x+1)(x+1)=200(x+1)2 t, 即y=200(x+1)2 . 答案:(1)A (2)D

导期 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)利润=销售单价×销售量.(×) (2)实际应用问题中自变量的取值范围由所得的函数解析式 唯一确定(X)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)利润=销售单价×销售量.( ) (2)实际应用问题中自变量的取值范围由所得的函数解析式 唯一确定.( ) × ×