
全程设计 3.1.2 函数的单调性 第1课时 单调性的定义与证明
3.1.2 函数的单调性 第1课时 单调性的定义与证明
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1.理解函数的单调区间、单调性等概念. 2.会划分函数的单调区间,判断单调性, 3.会用定义证明函数的单调性
导航 课标定位素养阐释 1.理解函数的单调区间、单调性等概念. 2.会划分函数的单调区间,判断单调性. 3.会用定义证明函数的单调性
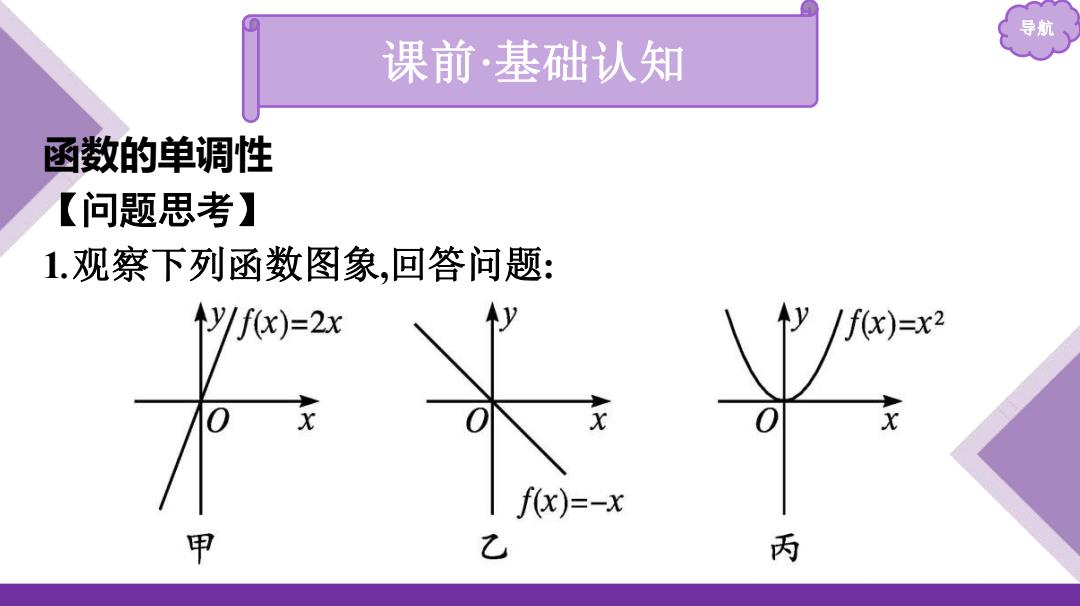
导航 课前·基础认知 函数的单调性 【问题思考】 1观察下列函数图象,回答问题: 个y/fx)=2x /f(x)=x2 f(x)=-x 甲 乙 丙
导航 课前 ·基础认知 函数的单调性 【问题思考】 1 .观察下列函数图象 ,回答问题 :

(1)从图象上看,当自变量x增大时,函数fx)的值如何变化? 提示:在甲图中,函数fx)的值随x的增大而增大 在乙图中,函数fx)的值随x的增大而减小 在丙图中,在y'轴左侧,函数x)的值随的增大而减小; 在y轴右侧,函数fx)的值随x的增大而增大 (2)在甲、乙图中,若xfx2) 3)在丙图中,若x1x2x1)<f2),则自变量x属于哪个区间? 提示:(0,+0)
导航 (1)从图象上看,当自变量x增大时,函数f(x)的值如何变化? 提示:在甲图中,函数f(x)的值随x的增大而增大. 在乙图中,函数f(x)的值随x的增大而减小. 在丙图中,在y轴左侧,函数f(x)的值随x的增大而减小; 在y轴右侧,函数f(x)的值随x的增大而增大. (2)在甲、乙图中,若x1f(x2 ). (3)在丙图中,若x1<x2 ,f(x1 )<f(x2 ),则自变量x属于哪个区间? 提示:(0,+∞)

导期 2.填空: 一 般地,设函数y=fx)的定义域为D,且ICD: (1)如果对任意x1水2∈I,当x1<x2时,都有 ,则称y=fx) 在I上是增函数(也称在I上单调递增); (2)如果对任意x1水2∈I,当x1<x2时,都有 ,则称y=x) 在I上是减函数(也称在I上单调递减), 两种情况下,都称函数在I上具有 (当为区间时,称为函 数的单调区间,也可分别称为单调递增区间或单调递减区间)
导航 2.填空: 一般地,设函数y=f(x)的定义域为D,且I⊆D: (1)如果对任意x1 ,x2∈I,当x1f(x2 ) ,则称y=f(x) 在I上是减函数(也称在I上单调递减). 两种情况下,都称函数在I上具有单调性(当I为区间时,称I为函 数的单调区间,也可分别称为单调递增区间或单调递减区间)
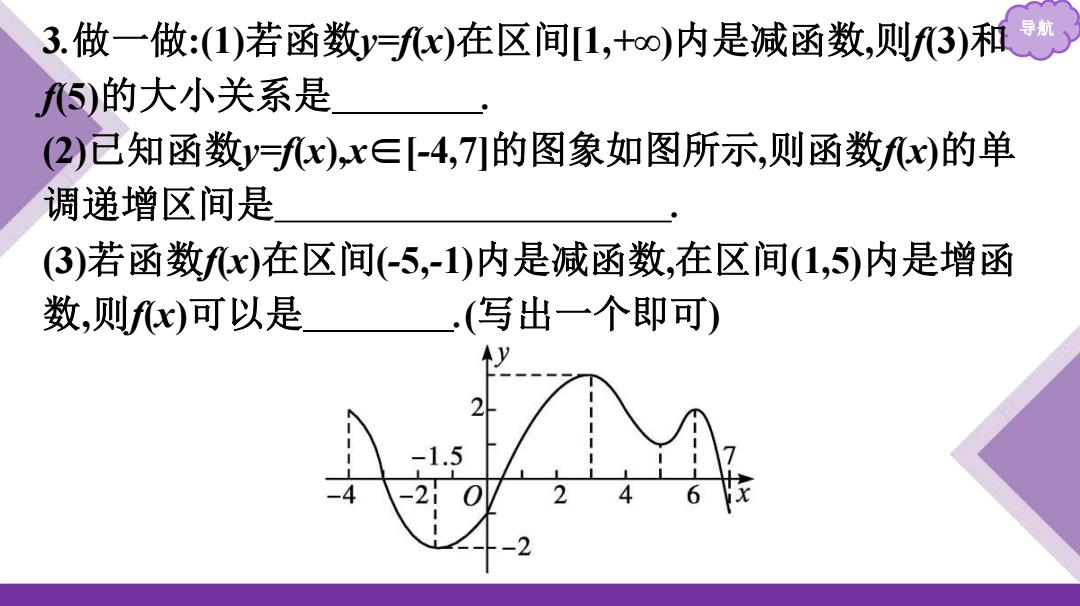
3.做一做:(1)若函数y=fx)在区间1,+∞)内是减函数,则f3)和 ⑤)的大小关系是 (2)已知函数y=fx),x∈[-4,7]的图象如图所示,则函数fx)的单 调递增区间是 (3)若函数fx)在区间(-5,-1)内是减函数,在区间(1,5)内是增函 数,则fx)可以是 (写出一个即可)
导航 3.做一做:(1)若函数y=f(x)在区间[1,+∞)内是减函数,则f(3)和 f(5)的大小关系是 . (2)已知函数y=f(x),x∈[-4,7]的图象如图所示,则函数f(x)的单 调递增区间是 . (3)若函数f(x)在区间(-5,-1)内是减函数,在区间(1,5)内是增函 数,则f(x)可以是 .(写出一个即可)

导航 解析:(1)因为函数y=x)在区间[1,十o)内是减函数,35) (2)由图象知,fx)的单调递增区间为[-1.5,3]和[5,6. 答案:(13)>5) (2)[-1.5,3]和[5,6] (3)x)=x2(答案不唯一)
导航 解析:(1)因为函数y=f(x)在区间[1,+∞)内是减函数,3f(5). (2)由图象知,f(x)的单调递增区间为[-1.5,3]和[5,6]. 答案:(1)f(3)>f(5) (2)[-1.5,3]和[5,6] (3)f(x)=x2 (答案不唯一)

【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“V,错误 的画“X” (1)如果函数fx)在区间(a,b)和(c,)内都是减函数,则fx)在区 间(a,b)U(c,)内是减函数.(X) (2)用定义证明函数的单调性时,可设x2,也可设x1>x2(√) 3)证明函数的单调性时,在该区间内取几个值验证一下即可 (X)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)如果函数f(x)在区间(a,b)和(c,d)内都是减函数,则f(x)在区 间(a,b)∪(c,d)内是减函数.( ) (2)用定义证明函数的单调性时,可设x1x2 . ( ) (3)证明函数的单调性时,在该区间内取几个值验证一下即可. ( ) × √ ×

导 课堂·重难突破 探究一由函数的图象确定函数的单调性或单调区间 【例1】作出函数fx)=x2+2x-31的图象,并指出其单调区间, 解:令g(x)=x2+2x-3=(x+1)2-4 先作出g()的图象,保留其在x轴及x轴上方部分, -2 把它在x轴下方的图象翻到轴上 -10123x 方就得到fx)=x2+2x-3的图象,如图所示. 由图象易得,函数fx)的单调递增区间是[-3,-1],1,+oo);函数c 的单调递减区间是(-o0,-3],1,1
导航 课堂·重难突破 探究一由函数的图象确定函数的单调性或单调区间 【例1】作出函数f(x)=|x2+2x-3|的图象,并指出其单调区间. 解:令g(x)=x2+2x-3=(x+1)2 -4. 先作出g(x)的图象,保留其在x轴及x轴上方部分, 把它在x轴下方的图象翻到x轴上 方就得到f(x)=|x2+2x-3|的图象,如图所示. 由图象易得,函数f(x)的单调递增区间是[-3,-1],[1,+∞);函数f(x) 的单调递减区间是(-∞,-3],[-1,1]