
全程设计 2.2.3 一元二次不等式的解法
2.2.3 一元二次不等式的解法
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.了解一元二次不等式的概念 2.掌握解一元二次不等式的两种方法:因式分解法和配方法. 3.会解简单的分式不等式 4.加强逻辑推理和数学运算能力的培养
导航 课标定位素养阐释 1.了解一元二次不等式的概念. 2.掌握解一元二次不等式的两种方法:因式分解法和配方法. 3.会解简单的分式不等式. 4.加强逻辑推理和数学运算能力的培养

导航 课前·基础认知 一元二次不等式的概念 【问题思考】 1.下列式子是关于x的不等式,且x的最高次幂为2的 是 (填序号) ①x2+2x-1=0;②x2≤5; ③x2.34-2x. 提示:②
导航 课前·基础认知 一、一元二次不等式的概念 【问题思考】 1.下列式子是关于x的不等式,且x的最高次幂为2的 是 .(填序号) ①x 2+2x-1=0; ②x 2≤5; ③ax2 -34-2x. 提示:②
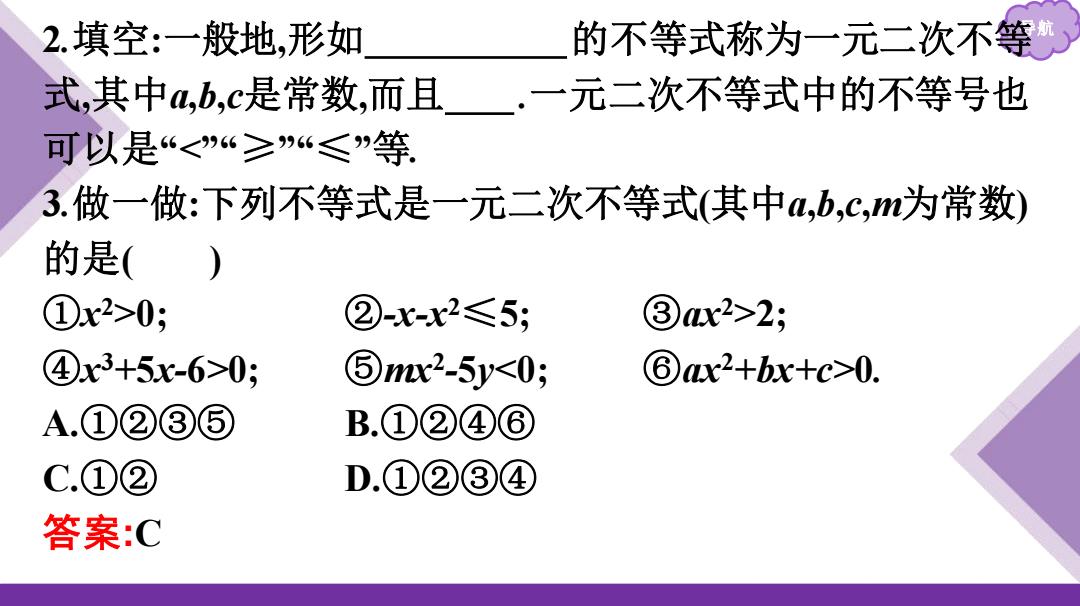
2.填空:一般地,形如 的不等式称为一元二次不等 式,其中,b,c是常数,而且·一元二次不等式中的不等号也 可以是“0; ②-x-x2≤5; ③x2>2; ④x3+5x-6>0; ⑤mx2-5y0. A.①②③⑤ B.①②④⑥ C.①② D.①②③④ 答案:C
导航 2.填空:一般地,形如ax2+bx+c>0 的不等式称为一元二次不等 式,其中a,b,c是常数,而且 a≠0 .一元二次不等式中的不等号也 可以是“0; ②-x-x 2≤5; ③ax2>2; ④x 3+5x-6>0; ⑤mx2 -5y0. A.①②③⑤ B.①②④⑥ C.①② D.①②③④ 答案:C

导航 二、利用因式分解法解一元二次不等式 【问题思考】 1.试将代数式x2-2x-3因式分解 提示x2-2x-3=(x-3)x+1). 2.若x2-2x-3>0,则x-3与x+1的符号如何? 提示a3与+1同号,即80或30 x+10的解集是
导航 二、利用因式分解法解一元二次不等式 【问题思考】 1.试将代数式x 2 -2x-3因式分解. 提示:x 2 -2x-3=(x-3)(x+1). 2.若x 2 -2x-3>0,则x-3与x+1的符号如何? 提 示:x-3 与 x+1同号,即 𝒙-𝟑 > 𝟎, 𝒙+ 𝟏 > 𝟎 或 𝒙-𝟑 0的解集是(-∞,x1 )∪(x2 ,+∞)

导航 4.解下列不等式: (1)x2-5x+6>0; (2)x2+6x+50,所以所求不等式的解 集为(-o0,2)U(3,+∞) (2)因为原不等式等价于(x+1)c+5)<0, 所以所求不等式的解集为(-5,-1)
导航 4.解下列不等式: (1)x 2 -5x+6>0; (2)x 2+6x+50,所以所求不等式的解 集为(-∞,2)∪(3,+∞). (2)因为原不等式等价于(x+1)(x+5)<0, 所以所求不等式的解集为(-5,-1)

导航 三、利用配方法解一元二次不等式 【问题思考】 1.能否将式子x2+bx+c(0)配成完全平方式? 提示:能.am+hctc=(x+)2+ ac-b2 4a 2.直接说出下列不等式的解集: (1)x2>mm>0); (2)x20). 提示:(1)(-o,VmU(Vm,+o);2)(Vm,Vm
导航 三、利用配方法解一元二次不等式 【问题思考】 1.能否将式子ax2+bx+c(a≠0)配成完全平方式? 提 示:能.ax2 +bx+c=a 𝒙 + 𝒃 𝟐𝒂 𝟐 + 𝟒𝒂𝒄-𝒃 𝟐 𝟒𝒂 . 2.直接说出下列不等式的解集: (1)x 2>m(m>0); (2)x 20). 提示:(1)(-∞, - 𝒎)∪( 𝒎,+∞);(2)(- 𝒎, 𝒎)

3.填空:一元二次不等式x2+bx+c>0(呋0)通过配方总是可以 变为(c-)2>k或x-)20时,c-)>k的解集为 (x-)2k的解集为 ;x-h)2k的解集为_;-)2<k的解集为_
导航 3.填空:一元二次不等式ax2+bx+c>0(a≠0)通过配方总是可以 变为(x-h) 2>k或(x-h) 20 时, (x-h) 2 > k 的解集为 (-∞,h- 𝒌) ∪ (h + 𝒌,+∞) ; (x-h) 2 k的解集为(-∞,h)∪(h,+∞);(x-h) 2k的解集为 R ;(x-h) 2<k的解集为 ⌀

导航 4解下列不等式: (1)x2.4x+3≥0; (2)x2+2x-4<0. 解:(1)由x2-4x+3≥0,得x-2)2≥1, 解得x≥3或x≤1. 故原不等式的解集为(-oo,1]U[3,+0) (2)由x2+2x-4<0,得(c+1)2<5, 解得-1-v5<<-1hv5. 故原不等式的解集为(1-v5,1+v√5
导航 4 .解下列不等式 : (1)x 2 - 4x+ 3 ≥0; (2)x 2 + 2 x - 4 < 0 . 解 :(1) 由 x 2 - 4x+ 3 ≥0, 得 (x -2) 2 ≥1, 解得x ≥ 3 或 x ≤ 1 . 故原不等式的解集为 ( - ∞,1] ∪[3,+∞ ) . (2) 由 x 2 + 2 x- 4 <0, 得 (x+1) 2 <5, 解 得-1- 𝟓<x<-1+ 𝟓. 故原不等式的解集为(-1- 𝟓,-1+ 𝟓)