
全程设计 第四章 数列 4.4* 数学归纳法
第四章 数列 4.4* 数学归纳法

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导航 素养·目标定位 目标素养 1.通过实例,了解数学归纳法的原理,提升数学抽象素养. 2.能用数学归纳法证明一些简单的数学命题,提升逻辑推理素 养
导航 目 标 素 养 1.通过实例,了解数学归纳法的原理,提升数学抽象素养. 2.能用数学归纳法证明一些简单的数学命题,提升逻辑推理素 养. 素养·目标定位
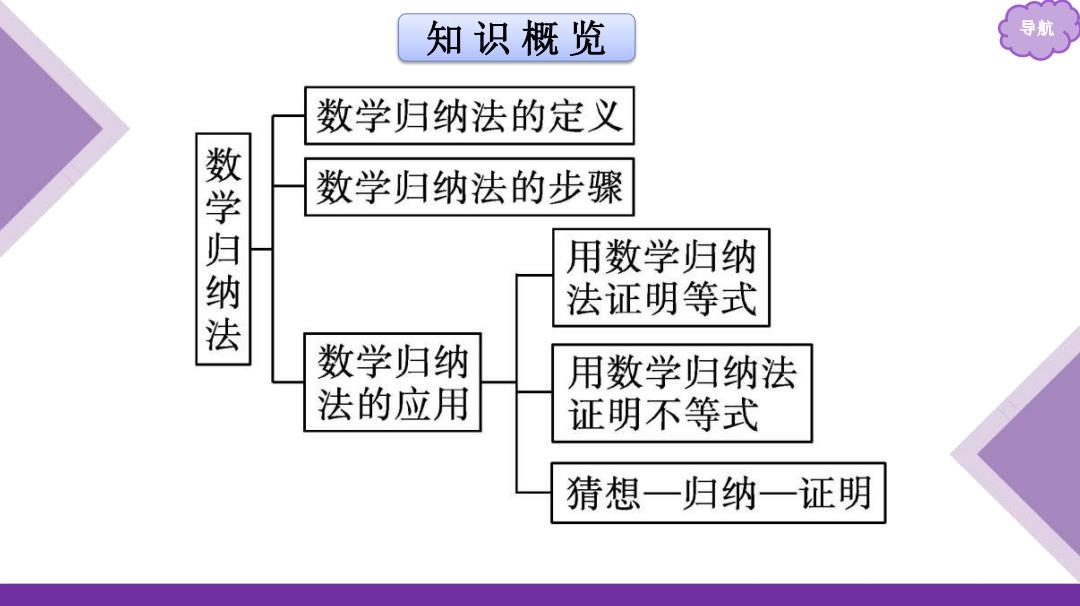
知识概览 导航 数学归纳法的定义 数学归纳 数学归纳法的步骤 用数学归纳 法证明等式 数学归纳 用数学归纳法 法的应用 证明不等式 猜想一归纳一证明
知 识 概 览 导航

导 课前·基础认知 1数学归纳法的定义 一 般地,证明一个与 n有关的命题,可按下列步骤 进行: (1)归纳奠基)证明当n=n(no∈N时命题成立; (2)归纳递推)以“当=k(k∈N*,k≥no)时命题成立”为条件, 推出“当 时命题也成立” 只要完成这两个步骤,就可以断定命题对从,开始的所有正 整数n都成立.这种证明方法称为数学归纳法
导航 1.数学归纳法的定义 一般地,证明一个与 正整数 n有关的命题,可按下列步骤 进行: (1)(归纳奠基)证明当n=n0 (n0∈N* )时命题成立; (2)(归纳递推)以“当n=k(k∈N* ,k≥n0 )时命题成立”为条件, 推出“当 n=k+1 时命题也成立” . 只要完成这两个步骤,就可以断定命题对从n0开始的所有正 整数n都成立.这种证明方法称为数学归纳法. 课前·基础认知

导航 微探究数学归纳法的第一步n的初始值是否一定为1? 提示:不一定,如证明n边形的内角和为(n-2)180°时,第一个 值为n=3
导航 微探究 数学归纳法的第一步n的初始值是否一定为1? 提示:不一定,如证明n边形的内角和为(n-2)·180°时,第一个 值为n0 =3
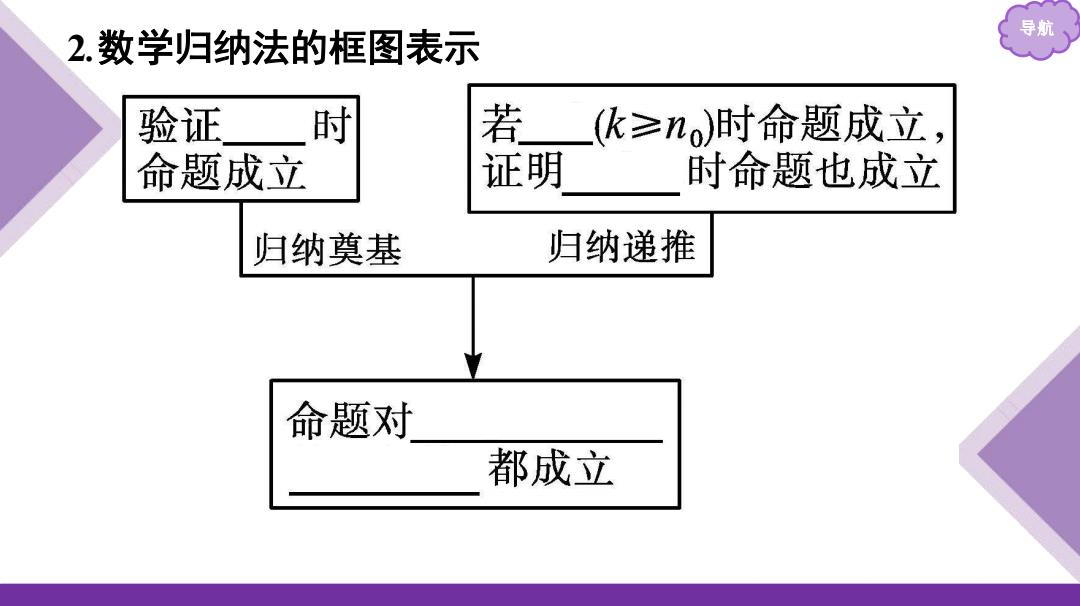
2.数学归纳法的框图表示 导航 验证 时 若(化≥)时命题成立 命题成立 证明 时命题也成立 归纳奠基 归纳递推 命题对 都成立
导航 2 .数学归纳法的框图表示

微总结数学归纳法证题的三个关键点 (1)验证是基础 数学归纳法的原理表明:第一个步骤是要找一个数no,这个o, 就是我们要证明的命题对象对应的最小自然数,这个自然数并 不一定都是“1”,因此“找准起点,奠基要稳”是第一个关键点 (2)递推是关键 数学归纳法的实质在于递推,故从“k”到“k+1”的过程中,要正 确分析式子项数的变化.关键是弄清等式两边的构成规律,弄 清由=k到n=k+1时,等式的两边会增加多少项,增加怎样的项
导航 微总结 数学归纳法证题的三个关键点 (1)验证是基础 数学归纳法的原理表明:第一个步骤是要找一个数n0 ,这个n0 , 就是我们要证明的命题对象对应的最小自然数,这个自然数并 不一定都是“1”,因此“找准起点,奠基要稳”是第一个关键点. (2)递推是关键 数学归纳法的实质在于递推,故从“k”到“k+1”的过程中,要正 确分析式子项数的变化.关键是弄清等式两边的构成规律,弄 清由n=k到n=k+1时,等式的两边会增加多少项,增加怎样的项

导期 3)假设是核心 在第二步证明=k+1成立时,一定要利用归纳假设,即必须把 归纳假设“=k时命题成立”作为条件来导出“n=k+1时命题也 成立”,在书写fk+1)时,一定要把包含f)的式子写出来,尤其 是)中的最后一项,这是数学归纳法的核心.不用归纳假设的 证明就不是数学归纳法
导航 (3)假设是核心 在第二步证明n=k+1成立时,一定要利用归纳假设,即必须把 归纳假设“n=k时命题成立”作为条件来导出“n=k+1时命题也 成立”,在书写f(k+1)时,一定要把包含f(k)的式子写出来,尤其 是f(k)中的最后一项,这是数学归纳法的核心.不用归纳假设的 证明就不是数学归纳法

微训练若命题A()n∈N的在n=k(k∈N的时成立,则有n=k+1 时命题成立.现知命题对n=no(no∈N时成立,则有(). A.命题对所有正整数都成立 B.命题对小于nn的正整数不成立,对大于或等于n的正整数 都成立 C.命题对小于,的正整数成立与否不能确定,对大于或等于 n的正整数都成立 D.以上说法都不正确 答案:C
导航 微训练 若命题A(n)(n∈N* )在n=k(k∈N* )时成立,则有n=k+1 时命题成立.现知命题对n=n0 (n0∈N* )时成立,则有( ). A.命题对所有正整数都成立 B.命题对小于n0的正整数不成立,对大于或等于n0的正整数 都成立 C.命题对小于n0的正整数成立与否不能确定,对大于或等于 n0的正整数都成立 D.以上说法都不正确 答案:C