
全程设计 1.集合与常用逻辑用语
1.集合与常用逻辑用语

梳理·构建体系 归纳·核心突破
梳理·构建体系 归纳·核心突破
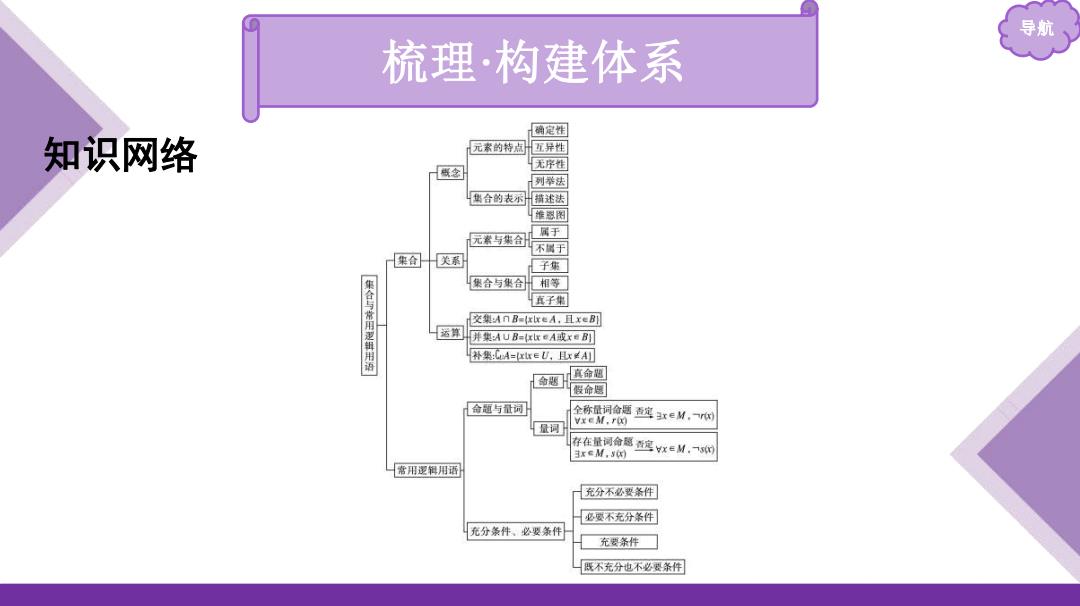
导航 梳理·构建体系 确定性 知识网络 元素的特点 互异性 无序性 列举法 货合的表闲 描述法 推恩图 元素与集合H 属于 不属于 集合 关系 子集 集合与集合相等】 集合与常用逻街用语 五子集 交集A门B=eA,且xeB] 并集AUB=在eA或xB] 补类:A=xr∈U,x装A 命巡命四 假命恩 命题与量词 全称量词命题香定xeM.一 量词 vreM.r) 存在量词命感香定x=M.一0 3xeM,s间 常用逐细用语 充分不必要条件 必爱不充分条件 充分条件、必要条件 充要条件☐ 既不充分也不必要条件
导航 梳理 ·构建体系 知识网络

导 要点梳理 1集合中的元素有哪三个特点?元素与集合之间的关系有哪 几种? 提示:确定性、互异性、无序性;属于和不属于 2.常见的数集符号有哪些? 提示:实数集R,有理数集Q,整数集Z,自然数集N,正整数集 N.N). 3.集合的表示方法有哪些? 提示:列举法、描述法、维恩图
导航 要点梳理 1.集合中的元素有哪三个特点?元素与集合之间的关系有哪 几种? 提示:确定性、互异性、无序性;属于和不属于. 2.常见的数集符号有哪些? 提示:实数集R,有理数集Q,整数集Z,自然数集N,正整数集 N+ (N* ). 3.集合的表示方法有哪些? 提示:列举法、描述法、维恩图
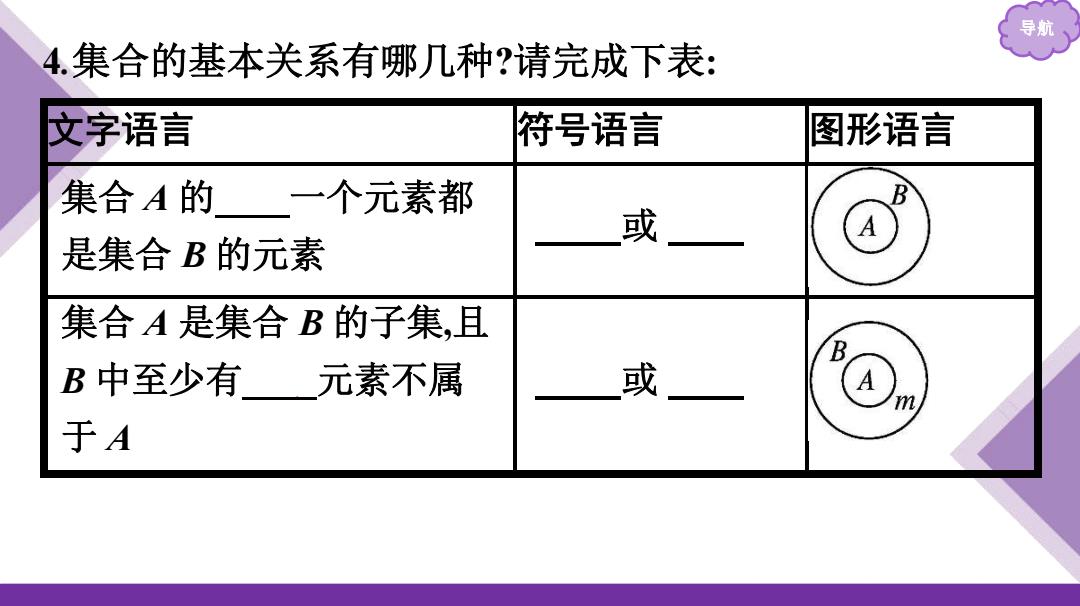
导航 4.集合的基本关系有哪几种?请完成下表: 文字语言 符号语言 图形语言 集合A的一个元素都 或 A 是集合B的元素 集合A是集合B的子集,且 B B中至少有元素不属 或 A) m 于A
导航 4 .集合的基本关系有哪几种 ?请完成下表: 文字语言 符号语言 图形语言 集合 A 的任意一个元素都 是集合 B 的元素 A ⊆B 或 B ⊇A 集合 A 是集合 B 的子集,且 B 中至少有一个元素不属 于 A A ⫋B 或 B ⫌A
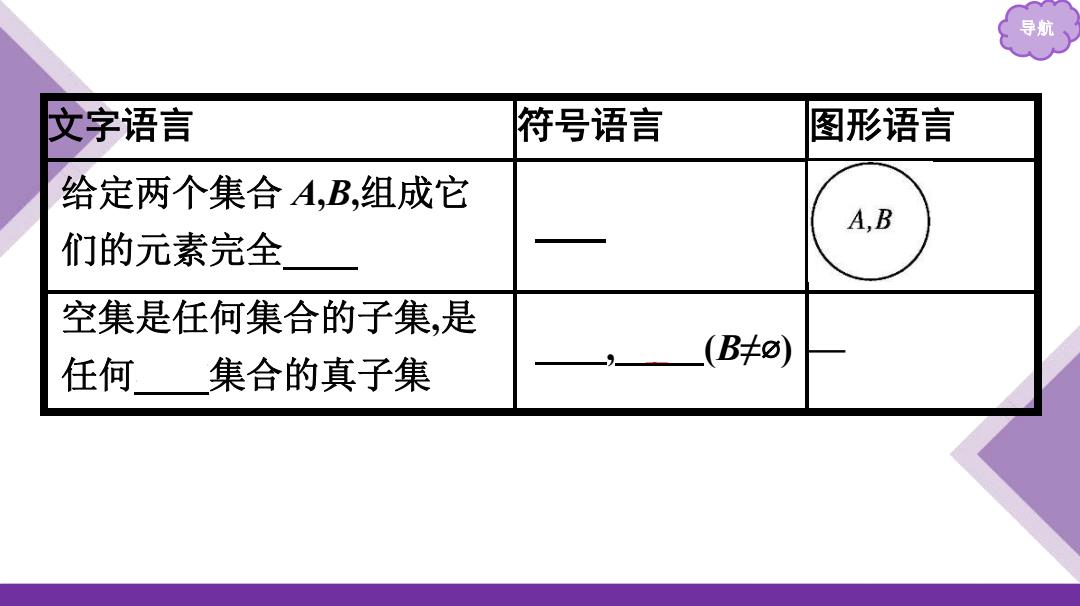
导航 文字语言 符号语言 图形语言 给定两个集合A,B,组成它 A,B 们的元素完全 空集是任何集合的子集,是 任何集合的真子集
导航 文字语言 符号语言 图形语言 给定两个集合 A,B,组成它 们的元素完全相同 A=B 空集是任何集合的子集,是 任何非空集合的真子集 ⌀⊆A, ⌀⫋B (B≠⌀) —
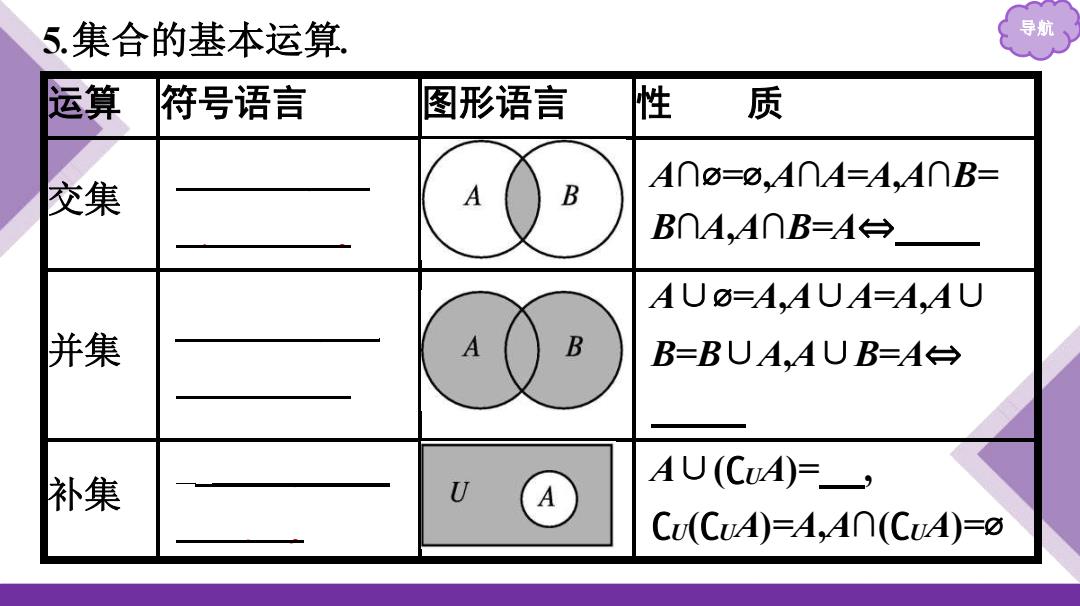
5.集合的基本运算 导航 运算} 符号语言 图形语言 性质 A∩⑦=⑦,A∩A=A,A∩B= 交集 B BnA,A∩B=A台 AU⑦=A,AUA=A,AU 并集 B B=BUA,AUB=A→ 补集 AU(CUA)=, A C(CA)=A,A∩(CA=o
导航 5 .集合的基本运算. 运算 符号语言 图形语言 性 质 交集 A ∩B={x|x ∈ A,且 x ∈ B} A ∩ ⌀ =⌀,A ∩A=A,A ∩B= B ∩ A,A ∩B=A ⇔ A ⊆B 并集 A ∪B={x|x ∈ A 或 x ∈ B} A ∪ ⌀=A,A ∪A=A,A ∪ B=B ∪ A,A ∪B=A ⇔ B⊆A 补集 ∁ UA={x|x ∈ U, 且 x∉A} A ∪(∁ UA)= U , ∁U(∁UA)=A,A∩(∁ UA)=⌀

导航 6.命题是如何定义的? 提示:可供真假判断的陈述语句就是命题, 7.全称量词命题和存在量词命题是什么?它们的否定是什么? 提示:全称量词命题记为:x∈M,x),其否定是:3x∈M,(x), 存在量词命题,记为:x∈M,sx),其否定是:x∈M,一Sx), 8.充分条件、必要条件、充要条件是如何定义的? 提示:若p→4,则p是q的充分条件,q是p的必要条件;若p→q,且 I→p,则p是q的充要条件
导航 6.命题是如何定义的? 提示:可供真假判断的陈述语句就是命题. 7.全称量词命题和存在量词命题是什么?它们的否定是什么? 提示:全称量词命题记为:∀x∈M,r(x),其否定是:∃x∈M, ¬r(x). 存在量词命题,记为:∃x∈M,s(x),其否定是:∀x∈M, ¬s(x). 8.充分条件、必要条件、充要条件是如何定义的? 提示:若p⇒q,则p是q的充分条件,q是p的必要条件;若p⇒q,且 q⇒p,则p是q的充要条件

导 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“X” (1)o={0}.(×) (2)oca.(√) 3)任何集合至少有两个子集(X) (4)N∩Q=N.(√) (5)若A={xK≥0},则CRA={xK≤0}.(×)
导航 【思考辨析】 判断下列说法是否正确,正确的在后面的括号内画“√”,错误 的画“×” . (1)⌀={0}.( ) (2)⌀⊆⌀.( ) (3)任何集合至少有两个子集.( ) (4)N∩Q=N.( ) (5)若A={x|x≥0},则∁RA={x|x≤0}.( ) × √ × √ ×

导航 (6)“k>0”是“y=x+b是增函数”的充要条件.(√) (7)“任何二次函数在其定义域上都是非奇非偶函数”的否定 是“有一个二次函数在其定义域上不是非奇非偶函数”.(√)
导航 (6)“k>0”是“y=kx+b是增函数”的充要条件.( ) (7)“任何二次函数在其定义域上都是非奇非偶函数”的否定 是“有一个二次函数在其定义域上不是非奇非偶函数” . ( ) √ √