
全程设计 5.3.2 函数的极值与最大(小)值 第1课时 函数的极值
5.3.2 函数的极值与最大(小)值 第1课时 函数的极值
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练

导 素养·目标定位 目标素养 1.了解函数极值的概念,会从几何方面直观理解函数的极值与 导数的关系,提升数学抽象核心素养 2.掌握函数极值的求法,掌握函数在某一点取得值的条件, 提升数学抽象、数学运算核心素养 3.能根据极值点与极值的情况求参数取值范围,会利用极值解 决方程的根与函数图象的交点个数问题,提升逻辑推理核心 素养
导航 目 标 素 养 1.了解函数极值的概念,会从几何方面直观理解函数的极值与 导数的关系,提升数学抽象核心素养. 2.掌握函数极值的求法,掌握函数在某一点取得极值的条件, 提升数学抽象、数学运算核心素养. 3.能根据极值点与极值的情况求参数取值范围,会利用极值解 决方程的根与函数图象的交点个数问题,提升逻辑推理核心 素养. 素养·目标定位
知识概览 导航 极值、极值点的概念 函数的极值 极值、极值点的求法 极值的应用
知 识 概 览 导航

导 课前·基础认知 1函数极值、极值点的概念 如图,函数y=fx)在点x=a的函数值f)比它在点 y x=附近其他点的函数值都小,f(@=0;而且在点=附近的左 侧 ,右侧 类似地,函数y=fx)在点x=b的 函数值fb)比它在点x=b附近其他点的函数值都大,f'b)=O;而 且在点x=b附近的左侧 ,右侧 .我们把a 叫做函数y=f)的极小值点,f孔a)叫做函数y=fx)的极小值;
导航 1.函数极值、极值点的概念 如图,函数y=f(x)在点x=a的函数值f(a)比它在点 x=a附近其他点的函数值都小,f'(a)=0;而且在点x=a附近的左 侧 f'(x)0 .类似地,函数y=f(x)在点x=b的 函数值f(b)比它在点x=b附近其他点的函数值都大,f'(b)=0;而 且在点x=b附近的左侧 f'(x)>0 ,右侧 f'(x)<0 .我们把a 叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值; 课前·基础认知

导航 b叫做函数y=fx)的极大值点,b)叫做函数y=fx)的极大值.极 小值点、极大值点统称为 ,极小值和极大值统称 为
导航 b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极 小值点、极大值点统称为 极值点 ,极小值和极大值统称 为 极值
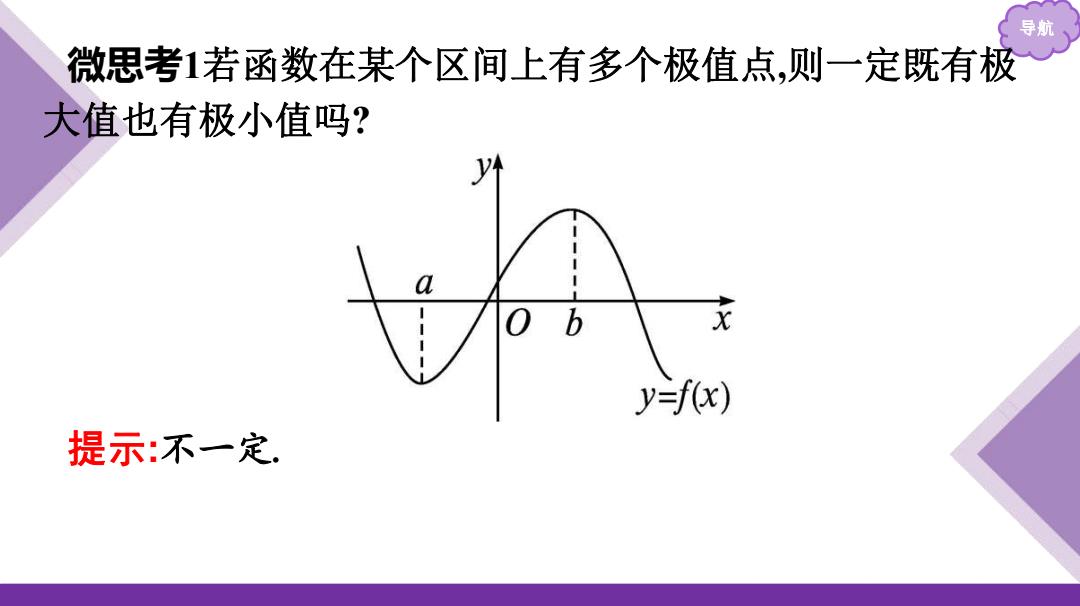
导航 微思考1若函数在某个区间上有多个极值点,则一定既有极 大值也有极小值吗? y a b y=f(x) 提示:不一定
导航 微思考1若函数在某个区间上有多个极值点,则一定既有极 大值也有极小值吗? 提示:不一定

导航 微训练1下列函数存在极值的是( 1 A0天 B.v=x-er C.y=2 D.v=x3 答案:B
导航 微训练 1下列函数存在极值的是 ( ). A.y = B.y=x - ex C.y = 2 D.y=x 3 答案 : B 𝟏𝒙

导航 2.函数极值的求法 解方程fx)=0,当fx)=0时: (1)如果在x附近的左侧fx)>0,右侧fx)0,那么x)是
导航 2.函数极值的求法 解方程f'(x)=0,当f'(x0 )=0时: (1)如果在x0附近的左侧f'(x)>0,右侧f'(x)0,那么f(x0 )是 极小值

导航 微思考2对于可导函数fx),若在某区间上存在极值点x,则x 能否为该区间的端点? 提示:不能
导航 微思考2对于可导函数f(x),若在某区间上存在极值点x0 ,则x0 能否为该区间的端点? 提示:不能