
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
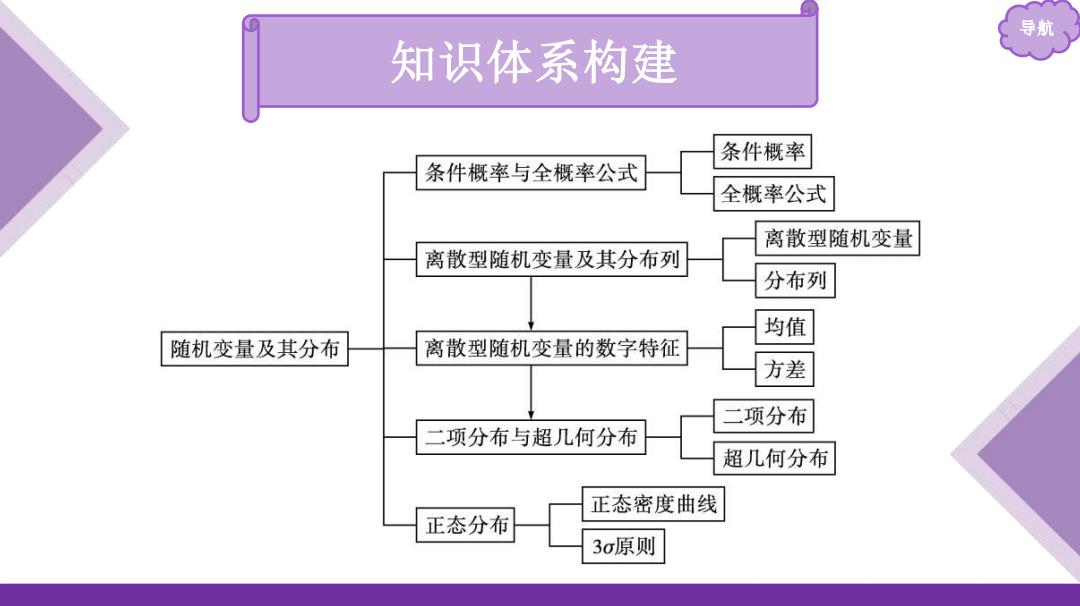
导航 知识体系构建 条件概率 条件概率与全概率公式 全概率公式 离散型随机变量 离散型随机变量及其分布列 分布列 均值 随机变量及其分布 离散型随机变量的数字特征 方差 二项分布 二项分布与超几何分布 超几何分布 正态密度曲线 正态分布 3σ原则
导航 知识体系构建

导 专题归纳突破 专题一条件概率 条件概率是学习相互独立事件的前提和基础,计算条件概率 时,必须弄清要求的条件概率是在什么条件下发生的概率 求条件概率主要有以下几种方法: (I)利用条件概率公式P(BA)Pan P(A) (2)针对古典概型,可通过缩减基本事件总数求解
导航 专题一 条件概率 条件概率是学习相互独立事件的前提和基础,计算条件概率 时,必须弄清要求的条件概率是在什么条件下发生的概率. 求条件概率主要有以下几种方法: (1)利用条件概率公式 P(B|A)= 𝑷(𝑨⋂𝑩) 𝑷(𝑨) ; (2)针对古典概型,可通过缩减基本事件总数求解. 专题归纳突破

导航 【典型例题1】设b和c分别是先后抛掷一枚骰子(六点)得到 的点数,用随机变量表示方程x2+bx+c=0实根的个数(重根按 一个计).求在先后两次出现的点数中有5的条件下,方程 x2+bx+c=0有实根的概率 解:记“先后两次出现的点数中有5”为事件M,则样本空间2 包含36个等可能的样本点.其中先后两次出现的点数中有5,样 本点数为11. 从而PM0-3 1
导航 【典型例题1】设b和c分别是先后抛掷一枚骰子(六点)得到 的点数,用随机变量ξ表示方程x 2+bx+c=0实根的个数(重根按 一个计).求在先后两次出现的点数中有5的条件下,方程 x 2+bx+c=0有实根的概率. 解:记“先后两次出现的点数中有5”为事件M,则样本空间Ω 包含36个等可能的样本点.其中先后两次出现的点数中有5,样 本点数为11. 从而 P(M)= 𝟏𝟏 𝟑𝟔

记“方程x2+bx+c=0有实根”为事件N, 导航 若使方程x2+bx+c=0有实根, 则=b2.4c≥0,即b≥2c. b,c分别是先后抛掷一枚骰子得到的点数, .当先后两次出现的点数中有5时, 若b=5,则c=1,2,3,4,5,6;若c=5,则b=5,6. b=5,5只能茅一种情况,从而PM)品 .在先后两次出现的点数中有5的条件下, 方程r24hrt+c0有实根的概率为(MIM)-PM 7 (M) =
记 导航 “方程x2+bx+c=0有实根”为事件N, 若使方程x 2+bx+c= 0有实根 , 则Δ=b 2 - 4 c ≥0, 即 b ≥2 . ∵ b , c分别是先后抛掷一枚骰子得到的点数 , ∴当先后两次出现的点数中有 5 时 , 若b=5, 则c=1,2,3,4,5,6 ; 若c=5, 则b=5,6 . 𝐜 b=5,c= 5 只能算一种情况,从而 P(MN)= 𝟕𝟑𝟔. ∴在先后两次出现的点数中有 5 的条件下, 方程 x 2 +bx+c= 0 有实根的概率为 P(N|M)= 𝑷(𝑴 𝑵) 𝑷(𝑴) = 𝟕𝟏𝟏

导 专题二离散型随机变量的分布列、均值和方差 1.含义:均值和方差分别反映了随机变量取值的平均水平及 其稳定性 2.应用范围:均值和方差在实际优化问题中应用非常广泛,如 同等资金下比较收益的高低、相同条件下比较质量的优劣、 性能的好坏等
导航 专题二 离散型随机变量的分布列、均值和方差 1.含义:均值和方差分别反映了随机变量取值的平均水平及 其稳定性. 2.应用范围:均值和方差在实际优化问题中应用非常广泛,如 同等资金下比较收益的高低、相同条件下比较质量的优劣、 性能的好坏等

3.求解思路:应用时,首先要将实际问题数学化,然后求出随 机变量的概率分布列.对于一般类型的随机变量,应先求其分 布列,再代入公式计算,此时解题的关键是概率的计算.计算概 率时要结合事件的特点,灵活地结合排列组合、古典概型、 独立重复试验概率、互斥事件和相互独立事件的概率等知识 求解若离散型随机变量服从特殊分布(如两点分布、二项分 布等),则可直接代入公式计算其数学期望与方差
导航 3.求解思路:应用时,首先要将实际问题数学化,然后求出随 机变量的概率分布列.对于一般类型的随机变量,应先求其分 布列,再代入公式计算,此时解题的关键是概率的计算.计算概 率时要结合事件的特点,灵活地结合排列组合、古典概型、 独立重复试验概率、互斥事件和相互独立事件的概率等知识 求解.若离散型随机变量服从特殊分布(如两点分布、二项分 布等),则可直接代入公式计算其数学期望与方差

【典型例题2】某产品按行业生产标准分成8个等级,等级系 数X依次为1,2,…,8,其中X≥5为标准A,X≥3为标准B.已知甲 厂执行标准A生产该产品,产品的零售价为6元件;乙厂执行 标准B生产该产品,产品的零售价为4元件,假定甲、乙两厂的 产品都符合相应的执行标准 ()已知甲厂产品的等级系数X的分布列如下表: 5 6 8 0.4 b 0.1 且X的均值EX1)=6,求,b的值;
导航 【典型例题2】某产品按行业生产标准分成8个等级,等级系 数X依次为1,2,…,8,其中X≥5为标准A,X≥3为标准B.已知甲 厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行 标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂的 产品都符合相应的执行标准. (1)已知甲厂产品的等级系数X1的分布列如下表: X1 5 6 7 8 P 0.4 a b 0.1 且X1的均值E(X1 )=6,求a,b的值;

导 2)为分析乙厂产品的等级系数X,从该厂生产的产品中随 机抽取30件,相应的等级系数组成一个样本,数据如下: 3533855 6 34 634 7 5 34853 834344756 7 用该样本的频率分布估计总体分布,将频率视为概率,求等 级系数X的均值;
导航 (2)为分析乙厂产品的等级系数X2 ,从该厂生产的产品中随 机抽取30件,相应的等级系数组成一个样本,数据如下: 3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7 用该样本的频率分布估计总体分布,将频率视为概率,求等 级系数X2的均值;