
全程设计 数学探究杨辉三角的性质与应用
数学探究 杨辉三角的性质与应用
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随 堂 训 练
导航 素养·目标定位 目标素养 探索并理解杨辉三角的性质及应用. 知识概览 杨辉三角的定义 杨辉三角的性质与应用 杨辉三角的性质 杨辉三角的应用
导航 目 标 素 养 探索并理解杨辉三角的性质及应用. 素养·目标定位 知 识 概 览

导航 课前·基础认知 1.杨辉三角 我国南宋数学家杨辉1261年所著 的《详解九章算法》一书中,把二项 (a+b) 式系数图形化,使组合数内在的一些 …1 代数性质直观地体现出来 (a+b)4 …1 (a+b)3 …1 5 10 (a+b)"展开式中的二项式系数,当n (a+b)5 …1615 20 15 依次取1,2,3,…时,如图所示: 上图称为杨辉三角(或帕斯卡三角)
导航 1 .杨辉三角 我国南宋数学家杨辉1261年所著 的《详解九章算法》一书中 ,把二项 式系数图形化 ,使组合数内在的一些 代数性质直观地体现出来 . (a+b ) n展开式中的二项式系数 , 当 n 依次取1,2,3, … 时 ,如图所示 : 上图称为杨辉三角 (或帕斯卡三角 ). 课前 ·基础认知

导 2.杨辉三角的特点 观察杨辉三角的相邻两行,可以发现,三角形的两个腰都是 由数字1组成的,其余的数都等于它肩上的两个数相加之和,即 Cn= 微思考根据杨辉三角的特点,在杨辉三角同一行中与两个1 等距离的项的系数相等,你可以得到二项式系数的什么性质? 提示:对称性,即C=C-m,也可以从函数)=C7的图象中得到
导航 2.杨辉三角的特点 观察杨辉三角的相邻两行,可以发现,三角形的两个腰都是 由数字1组成的,其余的数都等于它肩上的两个数相加之和,即 𝐂𝒏 𝒓 = 𝐂𝒏-𝟏 𝒓-𝟏 + 𝐂𝒏-𝟏 𝒓 . 微思考根据杨辉三角的特点,在杨辉三角同一行中与两个1 等距离的项的系数相等,你可以得到二项式系数的什么性质? 提示:对称性,即𝐂𝒏 𝒎 = 𝐂𝒏 𝒏-𝒎 ,也可以从函数 f(r)=𝐂𝒏 𝒓 的图象中得到

导 微训练与杨辉三角有类似性质的三角形数垒如图所示,,b 是某行的前两个数,当=7时,b等于() 2 A.20 B.21 343 477 4 C.22 D.23 51114115 答案:C a b 解析:根据观察可知,每一行的第一个数和最后一个数都相 等,其余每个数都等于它“肩上”两个数的和.故b=6+16=22
导航 微训练 与杨辉三角有类似性质的三角形数垒如图所示,a,b 是某行的前两个数,当a=7时,b等于( ) A.20 B.21 C.22 D.23 答案:C 解析:根据观察可知,每一行的第一个数和最后一个数都相 等,其余每个数都等于它“肩上”两个数的和.故b=6+16=22

导航 课堂·重难突破 杨辉三角的简单应用 第0行 典例剖析 第1行 1.如图所示,杨辉三角中的第5行 第2行 第3行 除去两端数字1以外,均能被5整除, 第4行 则具有类似性质(第n行能被n整除) 第5行 1 10 10 的行是( A.第6行 B.第7行 C.第8行 D.第9行 答案:B
导航 一 杨辉三角的简单应用 典例剖析 1.如图所示,杨辉三角中的第5行 除去两端数字1以外,均能被5整除, 则具有类似性质(第n行能被n整除) 的行是( ) A.第6行 B.第7行 C.第8行 D.第9行 答案:B 课堂·重难突破

导航、 解析:由题意,第6行为1,6,15,20,15,6,1,第7行为1,7,21,35,35, 21,7,1,故第7行除去两端数字1以外,均能被7整除
导航 解析:由题意,第6行为1,6,15,20,15,6,1,第7行为1,7,21,35,35, 21,7,1,故第7行除去两端数字1以外,均能被7整除
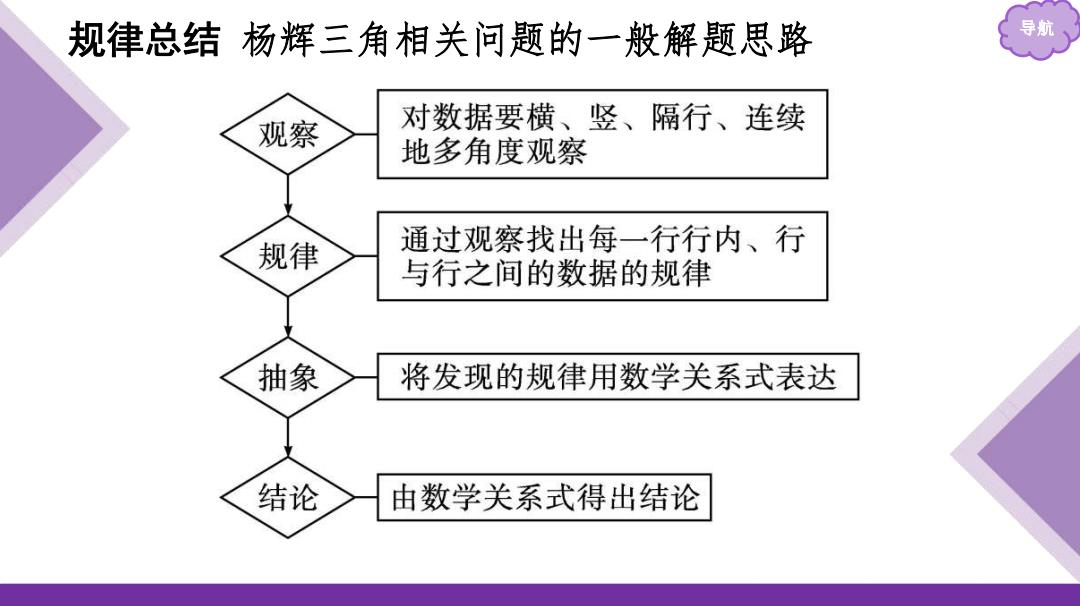
规律总结杨辉三角相关问题的一般解题思路 导航 观察 对数据要横、竖、隔行、连续 地多角度观察 规律 通过观察找出每一行行内、行 与行之间的数据的规律 抽象 将发现的规律用数学关系式表达 结论 由数学关系式得出结论
规律总结 杨辉三角相关问题的一般解题思路 导航

导期 学以致用 1.如图所示,由二项式系数构成的杨辉三角中,第 行 中从左至右的第14个数与第15个数的比为2:3. 第0行 第1行 第2行 2 第3行 3 第4行 1 6 4 第5行 1 10 5 答案34
导航 学以致用 1.如图所示,由二项式系数构成的杨辉三角中,第 行 中从左至右的第14个数与第15个数的比为2∶3. 答案:34