
全程设计 2.2 直线的方程 2.2.1 直线的点斜式方程
2.2 直线的方程 2.2.1 直线的点斜式方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导 素养·目标定位 目标素养 1根据确定直线位置的几何要素,探索直线的点斜式方程 2.掌握直线方程的点斜式和斜截式,并会熟练应用. 3.了解截距的概念,了解直线的斜截式方程与一次函数的 关系 4.会用直线的点斜式方程和斜截式方程解决直线的平行 与垂直问题
导航 素养·目标定位 目 标 素 养 1.根据确定直线位置的几何要素,探索直线的点斜式方程. 2.掌握直线方程的点斜式和斜截式,并会熟练应用. 3.了解截距的概念,了解直线的斜截式方程与一次函数的 关系. 4.会用直线的点斜式方程和斜截式方程解决直线的平行 与垂直问题
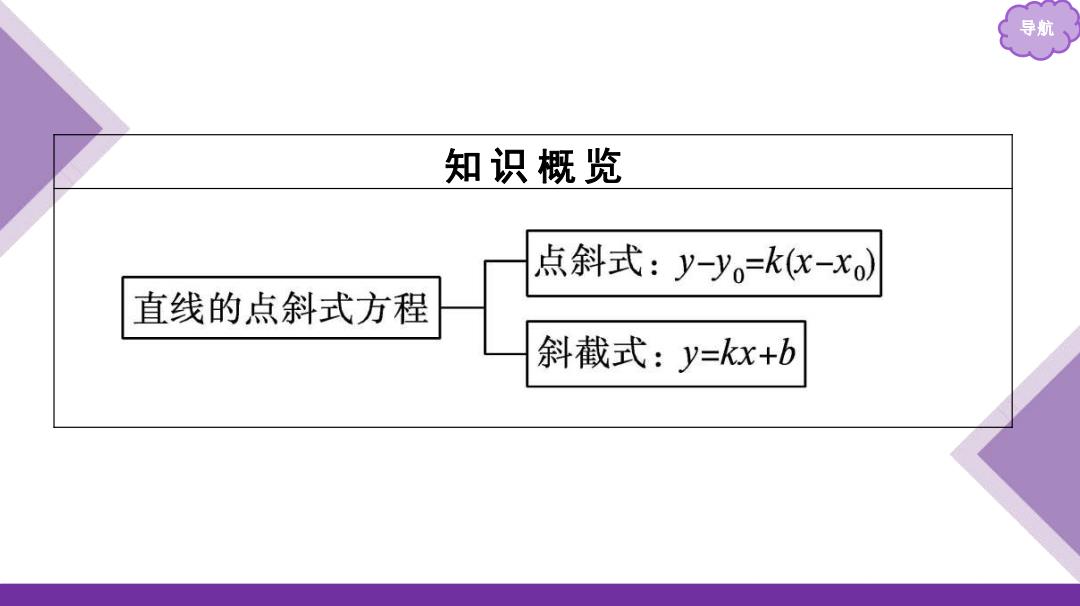
导航 知识概览 点斜式:y-yo=k(x-xo) 直线的点斜式方程 斜截式:y=kx+b
导航 知 识 概 览

导航 课前·基础认知 1,直线的点斜式方程 名称 点斜式 已知条件 点PKyo)和斜率k y P(o.yo) 示意图 方程 yy三 适用条件 斜率存在的直线
导航 课前·基础认知 1.直线的点斜式方程 名称 点斜式 已知条件 点P(x0 ,y0 )和斜率k 示意图 方程 y-y0= k(x-x0 ) 适用条件 斜率存在的直线

导期 微训练直线经过点P(2,-3),且倾斜角=45°,则直线的点斜式 方程是( A.y+3=x-2 B.v-3=x+2 Cy+2=x-3D.y-2=x+3 答案:A 解析:.直线l的斜率=tan45°=1, ∴.直线的方程为y+3=x-2
导航 微训练直线l经过点P(2,-3),且倾斜角α=45° ,则直线的点斜式 方程是( ) A.y+3=x-2 B.y-3=x+2 C.y+2=x-3 D.y-2=x+3 答案:A 解析:∵直线l的斜率k=tan 45° =1, ∴直线l的方程为y+3=x-2

导航 2.直线的斜截式方程 名称 斜截式 已知条件 斜率k和直线在y轴上的截距b 示意图 方程 适用条件 斜率存在的直线
导航 2.直线的斜截式方程 名称 斜截式 已知条件 斜率k和直线在y轴上的截距b 示意图 方程 y=kx+b 适用条件 斜率存在的直线

导 微训练在y轴上的截距为2,且与直线y=3x4平行的直线的斜 截式方程为 答案y=3x+2 解析:.直线y=3x-4的斜率为-3, 所求直线与此直线平行,斜率为-3, 又截距为2,∴.由斜截式方程可得y=3x+2
导航 微训练在y轴上的截距为2,且与直线y=-3x-4平行的直线的斜 截式方程为 . 答案:y=-3x+2 解析:∵直线y=-3x-4的斜率为-3, 所求直线与此直线平行,∴斜率为-3, 又截距为2,∴由斜截式方程可得y=-3x+2

导航 课堂·重难突破 一直线的点斜式方程 典例剖析 1.根据条件写出下列直线的点斜式方程: (1)过点A(-4,3),斜率=3; (2)经过点B(-1,4),倾斜角为135°; (3)过点D(2,1)和E3,-4)
导航 课堂·重难突破 一 直线的点斜式方程 典例剖析 1.根据条件写出下列直线的点斜式方程: (1)过点A(-4,3),斜率k=3; (2)经过点B(-1,4),倾斜角为135° ; (3)过点D(2,1)和E(3,-4)

导期 解:(1)由点斜式方程可知,所求直线方程为y-3=3x-(-4)小 (2)由题意知,直线的斜率=tan135°=-1,故所求直线的方程为 y-4=-(x+1). (3)直线过点D(2,1)和E3,-4), 斜率415. 3-2 由点斜式方程得y-1=-5c-2)或y+4=5x-3)
导航 解:(1)由点斜式方程可知,所求直线方程为y-3=3[x-(-4)]. (2)由题意知,直线的斜率k=tan 135° =-1,故所求直线的方程为 y-4=-(x+1). (3)直线过点D(2,1)和E(3,-4), 斜率 k=-𝟒-𝟏 𝟑-𝟐 =-5. 由点斜式方程得y-1=-5(x-2)或y+4=-5(x-3)