
全程设计 3.2 双曲线 3.2.1 双曲线及其标准方程
3.2 双曲线 3.2.1 双曲线及其标准方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 1.了解双曲线的实际背景,结合具体实际情景,理解并掌握双 曲线的定义,能够运用双曲线的定义解决问题, 2.掌握双曲线的标准方程,能根据条件求双曲线的标准方程 3.通过学习,提升直观想象和数学抽象的核心素养
导航 素养·目标定位 目 标 素 养 1.了解双曲线的实际背景,结合具体实际情景,理解并掌握双 曲线的定义,能够运用双曲线的定义解决问题. 2.掌握双曲线的标准方程,能根据条件求双曲线的标准方程. 3.通过学习,提升直观想象和数学抽象的核心素养
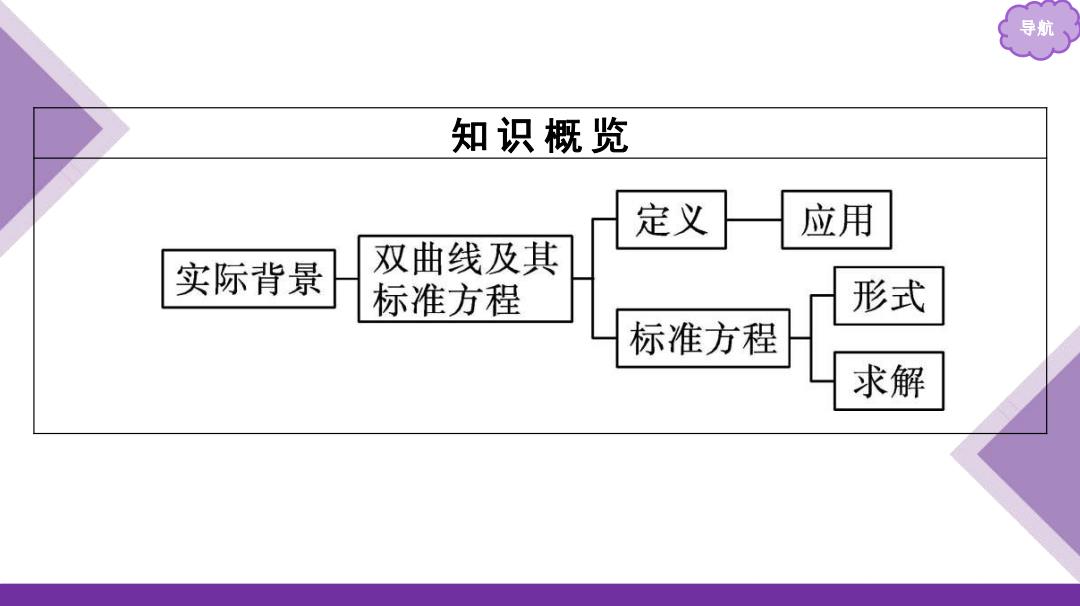
导航 知识概览 定义 应用 实际背景 双曲线及其 标准方程 形式 标准方程 求解
导航 知 识 概 览

导航 课前·基础认知 1双曲线的定义 一般地,平面内与两个定点F,F,的距离的 等 于非零常数(小于 )的点的轨迹叫做双曲线这两个 定点叫做双曲线的 ,两焦点间的距离叫做双曲线的
导航 课前·基础认知 1.双曲线的定义 一般地,平面内与两个定点F1 ,F2的距离的 差的绝对值 等 于非零常数(小于 |F1F2 | )的点的轨迹叫做双曲线.这两个 定点叫做双曲线的 焦点 ,两焦点间的距离叫做双曲线的 焦距

导 微训练已知两定点F1(3,0),F2(3,0),在平面内满足下列条件的 动点P的轨迹中,是双曲线的是( A.PF-PF2=5 B.PF-PF2=6 C.UPF-PF=7 D.PF-PF2-0 答案:A
导航 微训练已知两定点F1 (-3,0),F2 (3,0),在平面内满足下列条件的 动点P的轨迹中,是双曲线的是( ) A.||PF1 |-|PF2 ||=5 B.||PF1 |-|PF2 ||=6 C.||PF1 |-|PF2 ||=7 D.||PF1 |-|PF2 ||=0 答案:A
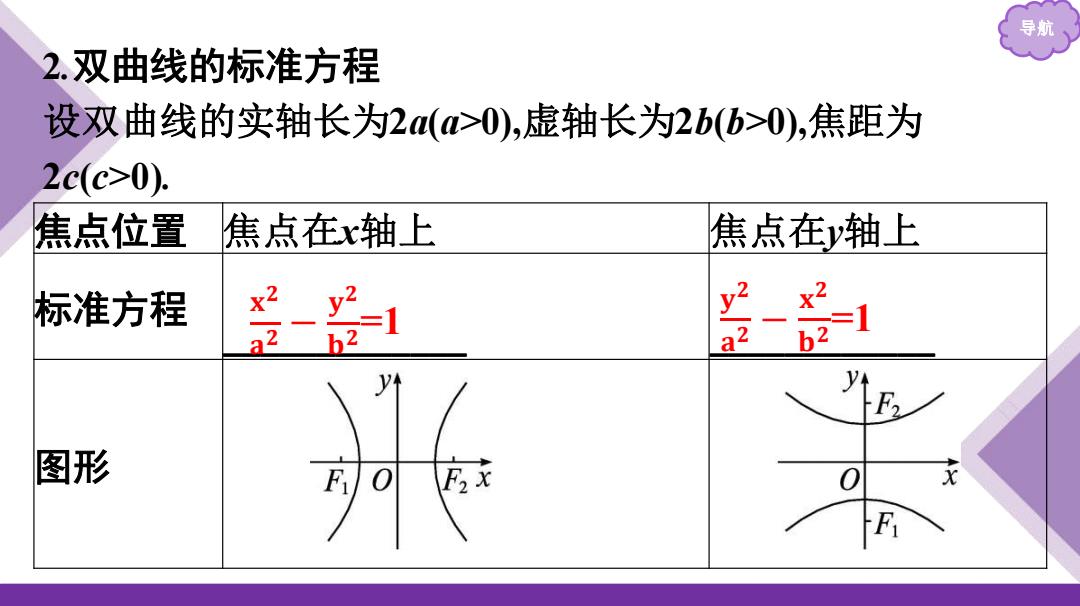
导航 2.双曲线的标准方程 设双曲线的实轴长为2a(>0),虚轴长为2b(b>0),焦距为 2c(c>0). 焦点位置 焦点在x轴上 焦点在y轴上 标准方程 y2 x2 b2 2 =1 b2 y 图形 F 0 0 F
导航 2.双曲线的标准方程 设双曲线的实轴长为2a(a>0),虚轴长为2b(b>0),焦距为 2c(c>0). 焦点位置 焦点在x轴上 焦点在y轴上 标准方程 _____________ ____________ 图形 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1
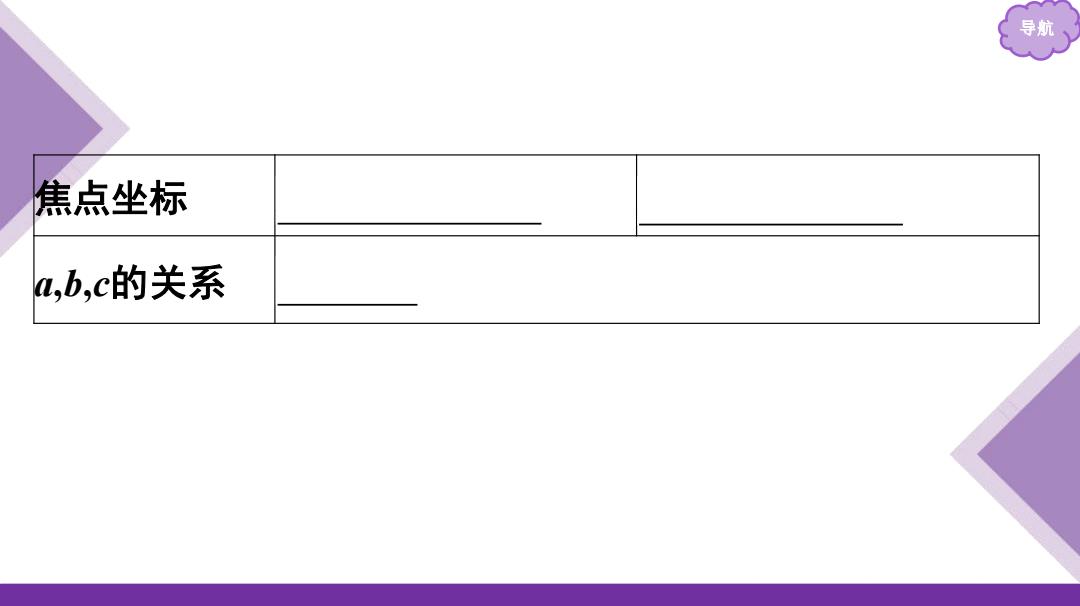
导航、 焦点坐标 m,b,c的关系
导航 焦点坐标 F1 (-c,0),F2 (c,0) F1 (0,-c),F2 (0,c) a,b,c的关系 c 2=a2+b2

徽探究双曲线方程的两种表示形式兰 h2 a2 21(>0,b>0)有何异同点?如何根据方程确定双曲线 的焦点位置?双曲线中参数,b,c的关系与椭圆相同吗? 提示:双曲线方程的两种表示形式器-片-15-号1 (>0,b>0)的相同点是:它们的形状、大小都相同,都有 >0,b>0,2+b2=c2.不同点是:两种双曲线的位置不同,它们的
导航 微探究 双曲线方程的两种表示形式𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃𝟐 =1, 𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃𝟐 =1(a>0,b>0)有何异同点?如何根据方程确定双曲线 的焦点位置?双曲线中参数 a,b,c 的关系与椭圆相同吗? 提示:双曲线方程的两种表示形式𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐 =1,𝒚 𝟐 𝒂𝟐 − 𝒙 𝟐 𝒃 𝟐 =1 (a>0,b>0)的相同点是:它们的形状、大小都相同,都有 a>0,b>0,a 2+b2=c2 .不同点是:两种双曲线的位置不同,它们的

导航 焦点坐标也不同.双曲线的焦点在x轴上台标准方程中x2项的 系数为正;双曲线的焦点在轴上曰标准方程中y2项的系数为 正,亦即“焦点跟着正项走”,这是判断双曲线焦点所在坐标轴 的重要方法;双曲线中参数4,b,c的关系为2+b2=C2,其中c的值 最大,,b的大小关系不确定,与椭圆中参数,b,c的关系不同
导航 焦点坐标也不同.双曲线的焦点在x轴上⇔标准方程中x 2项的 系数为正;双曲线的焦点在y轴上⇔标准方程中y 2项的系数为 正,亦即“焦点跟着正项走”,这是判断双曲线焦点所在坐标轴 的重要方法;双曲线中参数a,b,c的关系为a 2+b2=c2 ,其中c的值 最大,a,b的大小关系不确定,与椭圆中参数a,b,c的关系不同