
全程设计 2.4 圆的方程 2.4.1 圆的标准方程
2.4 圆的方程 2.4.1 圆的标准方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 知识概览 1.回顾确定圆的几何要素,在 平面直角坐标系中,探索并 圆的标准方程:x-a)2+y-b)2=r2 圆的 掌握圆的标准方程 标准 圆心(a,b),半径r 方程 2.会根据已知条件求圆的标 点与圆的位置关系:圆上,圆内,圆外 准方程 3.会判断点与圆的位置关系
导航 素养·目标定位 目 标 素 养 知 识 概 览 1.回顾确定圆的几何要素,在 平面直角坐标系中,探索并 掌握圆的标准方程. 2.会根据已知条件求圆的标 准方程. 3.会判断点与圆的位置关系

导期 课前·基础认知 1.圆的标准方程 ()圆的定义:圆是平面上到定点的距离等于 的点的 集合,定点称为 称为圆的半径用集合表示 为P={M (2)圆的标准方程:圆心为A(a,b),半径长为的圆的标准方程是 .当=b=0时,方程为x2+y2=2,表示以 为圆心、半径为的圆
导航 课前·基础认知 1.圆的标准方程 (1)圆的定义:圆是平面上到定点的距离等于 定长 的点的 集合,定点称为 圆心 , 定长 称为圆的半径.用集合表示 为P={M| |MA|=r }. (2)圆的标准方程:圆心为A(a,b),半径长为r的圆的标准方程是 (x-a) 2+(y-b) 2=r2 .当a=b=0时,方程为x 2+y2=r2 ,表示以 原点 为圆心、半径为r的圆

导航 微训练圆x-2)2+(y+3)2=2的圆心和半径分别是( A.(-2,3),1 B.(2,-3),3 C.(-2,3),V2 D.(2,-3),V2 答案:D 解析:由圆的标准方程可得圆心坐标为(2,3),半径为2
导航 微训练圆(x-2)2+(y+3)2=2的圆心和半径分别是( ) A.(-2,3),1 B.(2,-3),3 C.(-2,3), 𝟐 D.(2,-3), 𝟐 答案:D 解析:由圆的标准方程可得圆心坐标为(2,-3),半径为 𝟐
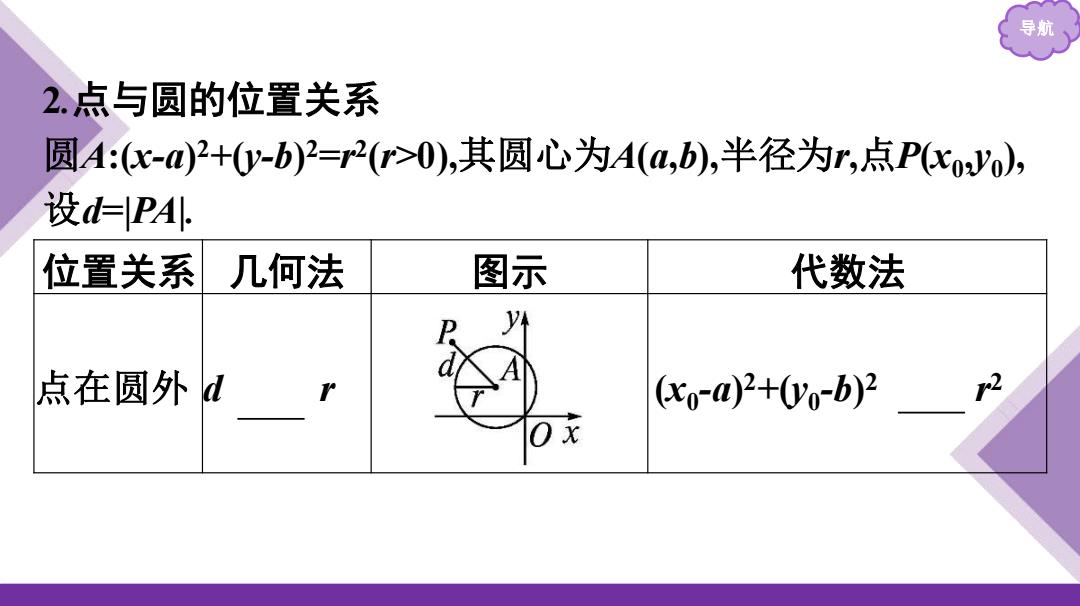
导航 2.点与圆的位置关系 圆Ac-)2+(y-b)2=r2(>0),其圆心为A(,b),半径为,点PKyo), 设d=PA 位置关系几何法 图示 代数法 点在圆外dr xo-02+(0y-b)22
导航 2.点与圆的位置关系 圆A:(x-a) 2+(y-b) 2=r2 (r>0),其圆心为A(a,b),半径为r,点P(x0 ,y0 ), 设d=|PA|. 位置关系 几何法 图示 代数法 点在圆外 d > r (x0 -a) 2+(y0 -b) 2 > r 2
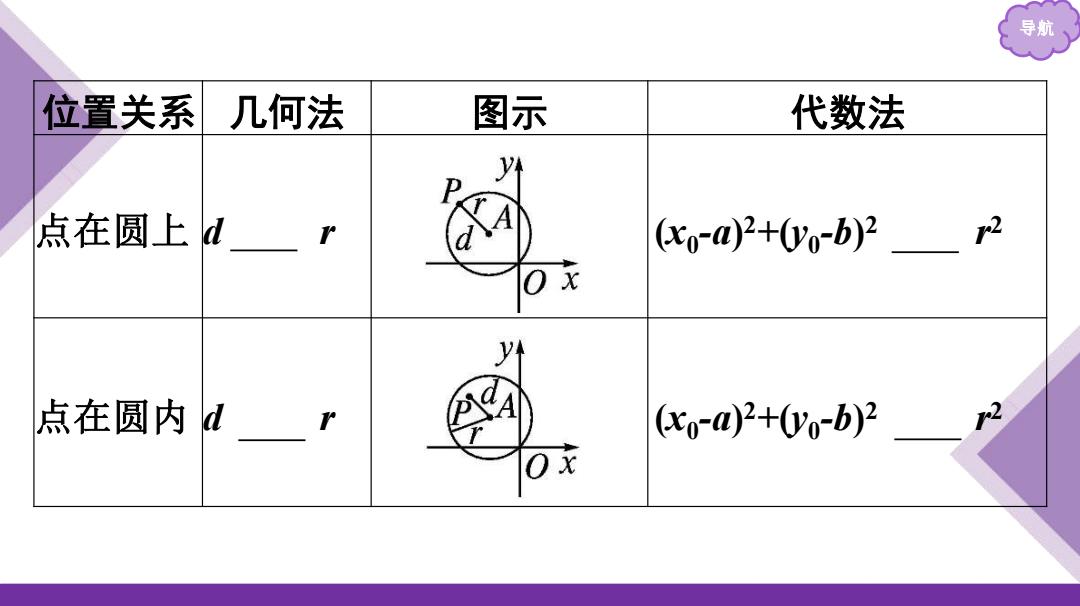
导航 位置关系几何法 图示 代数法 y外 点在圆上dr co-@2+0-b)22 点在圆内dr c0-a)2+0yo-b)2_r2
导航 位置关系 几何法 图示 代数法 点在圆上 d = r (x0 -a) 2+(y0 -b) 2 = r 2 点在圆内 d < r (x0 -a) 2+(y0 -b) 2 < r 2

导航 微思考(1)方程x-2+(y-b)2=2(4,b,∈R)表示一个圆吗?为什 么? (2)点A(1,1),B(-3,0),C(V2,V2)与圆x2+y2=4的位置关系如图所 示,则1OA,1OB,1OC与圆的半径=2是什么关系? B
导航 微思考(1)方程(x-a) 2+(y-b) 2=r2 (a,b,r∈R)表示一个圆吗?为什 么? (2)点A(1,1),B(-3,0),C( )与圆x 2+y2=4的位置关系如图所 示,则|OA|,|OB|,|OC|与圆的半径r=2是什么关系? 𝟐, 𝟐

导航 提示:(1)未必表示圆.当≠0时,表示圆心为(,b),半径为的圆; 当=0时,表示一个点(☑,b) (2)10A2,10C=2
导航 提示:(1)未必表示圆.当r≠0时,表示圆心为(a,b),半径为|r|的圆; 当r=0时,表示一个点(a,b). (2)|OA|2,|OC|=2

导航 课堂·重难突破 求圆的标准方程 典例剖析 1.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上 的圆的方程
导航 课堂·重难突破 一 求圆的标准方程 典例剖析 1.求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上 的圆的方程