
全程设计 3.2.2 双曲线的简单几何性质
3.2.2 双曲线的简单几何性质

素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导 素养·目标定位 目标素养 1.掌握双曲线的范围、对称性、顶点、渐近线、离心率等几 何性质 2.能够利用双曲线的几何性质解决有关问题! 3.掌握直线与双曲线的位置关系及其判断方法 4.通过学习,提升数学抽象、数学运算的核心素养
导航 素养·目标定位 目 标 素 养 1.掌握双曲线的范围、对称性、顶点、渐近线、离心率等几 何性质. 2.能够利用双曲线的几何性质解决有关问题. 3.掌握直线与双曲线的位置关系及其判断方法. 4.通过学习,提升数学抽象、数学运算的核心素养
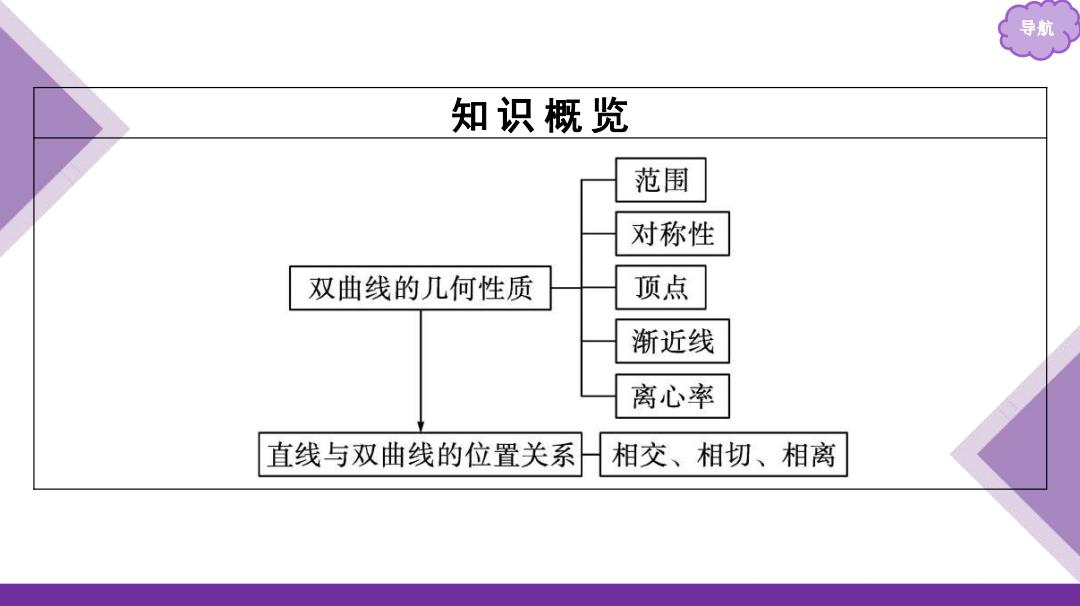
导航 知识概览 范围 对称性 双曲线的几何性质 顶点 渐近线 离心率 直线与双曲线的位置关系 相交、相切、相离
导航 知 识 概 览
导航 课前·基础认知 1.双曲线的几何性质 设双曲线的实轴长为2(a>0),虚轴长为2b(b>0),焦距为2c(c>0) 标准方程 b2 a2 B2 F2 图形 A2 Aza bi F 0 a BO4B,元 B ↑E
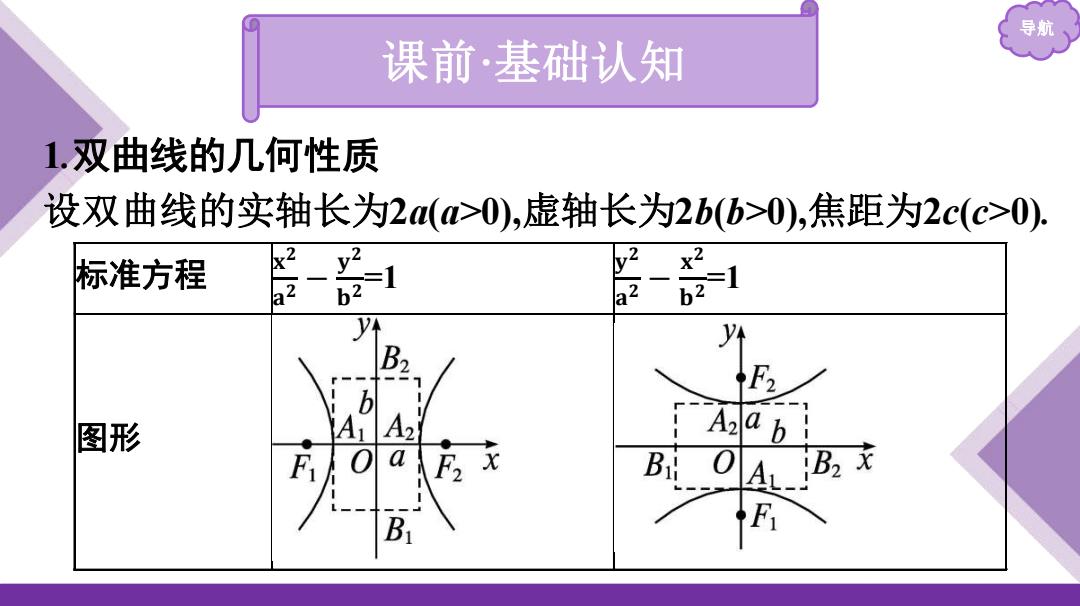
导航 课前·基础认知 1.双曲线的几何性质 设双曲线的实轴长为2a(a>0),虚轴长为2b(b>0),焦距为2c(c>0). 标准方程 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1 图形

导航 标准方程 x2 a2 1 范围 x≤-或x≥,y∈R x∈Ry≤-或y≥M 几 对称性 关于 对称 何 中心 0,0) 性质 顶点 A1(-a,0),A2(a,0) A1(0,-@),A2(0,@) 轴 线段A1A2叫做实轴,长度为 线段B,B,叫做虚轴,长度为
导航 标准方程 几 何 性 质 范围 x≤-a或x≥a,y∈R x∈R,y≤-a或y≥a 对称性 关于 x轴 , y轴 , 原点 对称 中心 (0,0) 顶点 A1 (-a,0),A2 (a,0) A1 (0,-a),A2 (0,a) 轴 线段A1A2叫做实轴,长度为 2a 线段B1B2叫做虚轴,长度为 2b 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1

导航 标准方程 2_ x2 a - b2 a2 =1 b2 几 焦点 F(c,0),F(c,0) F(0,-C,F0,c) 何 离心率 8,取值范围是e∈ 性 渐近线 y±鉴 ±
导航 标准方程 几 何 性 质 焦点 F1 (-c,0),F2 (c,0) F1 (0,-c),F2 (0,c) 离心率 e= ,取值范围是e∈ (1,+∞) 渐近线 𝐱 𝟐 𝐚 𝟐 − 𝐲 𝟐 𝐛 𝟐 =1 𝐲 𝟐 𝐚 𝟐 − 𝐱 𝟐 𝐛 𝟐 =1 𝒄 𝒂 y=± 𝒃 𝒂 x y=± 𝒂 𝒃 x

导 微探究是否存在实轴长与虚轴长相等的双曲线?它的渐近线、 离心率有何特点? 提示:当=b时,双曲线的实轴长与虚轴长相等,此时称为等轴 双曲线,等轴双曲线的渐近线方程为y=±北,两条渐近线互相垂 直,其离心率等于√2,其焦点可以在x轴上,也可以在轴上
导航 微探究 是否存在实轴长与虚轴长相等的双曲线?它的渐近线、 离心率有何特点? 提示:当a=b时,双曲线的实轴长与虚轴长相等,此时称为等轴 双曲线,等轴双曲线的渐近线方程为y=±x,两条渐近线互相垂 直,其离心率等于 𝟐 ,其焦点可以在x轴上,也可以在y轴上

导航 2.直线与双曲线的位置关系 直线与双曲线的位置关系有三种,分别是
导航 2.直线与双曲线的位置关系 直线与双曲线的位置关系有三种,分别是 相交 、 相切 、 相离

微解读如何判断直线与双曲线的位置关系? 提示:将直线方程Ax+By+C=O(A,B不同时为0)与双曲线方程 之 a2- =1(>0,b>0)联立,消去(或x),得到关于x(或y)的方程 x2+nx+p=0. (1)若0,则当方程有唯一解时,直线与双曲线有唯一交,点,直 线与双曲线的渐近线平行;当方程无解时,直线与双曲线相离, 此时直线为双曲线的渐近线。 (2)若0,记方程的判别式为4,①若>0,则直线与双曲线相 交;②若=0,则直线与双曲线相切;③若<0,则直线与双曲线 相离
导航 微解读 如何判断直线与双曲线的位置关系? 提示:将直线方程Ax+By+C=0(A,B不同时为0)与双曲线方程 =1(a>0,b>0)联立,消去y(或x),得到关于x(或y)的方程 mx2+nx+p=0. (1)若m=0,则当方程有唯一解时,直线与双曲线有唯一交点,直 线与双曲线的渐近线平行;当方程无解时,直线与双曲线相离, 此时直线为双曲线的渐近线. (2)若m≠0,记方程的判别式为Δ,①若Δ>0,则直线与双曲线相 交;②若Δ=0,则直线与双曲线相切;③若Δ<0,则直线与双曲线 相离. 𝒙 𝟐 𝒂𝟐 − 𝒚 𝟐 𝒃 𝟐