
全程设计 3.1 椭圆 3.1.1 椭圆及其标准方程
3.1 椭圆 3.1.1 椭圆及其标准方程
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练
素养·目标定位 课前·基础认知 课堂·重难突破 随堂训练

导航 素养·目标定位 目标素养 1.了解椭圆的实际背景,结合具体实际情景,理解并掌握椭 圆的定义,能够运用椭圆的定义解决问题 2.掌握椭圆的标准方程,能根据条件求椭圆的标准方程 3.掌握用相关点法求动点轨迹方程的方法 4.通过学习,提升直观想象和数学抽象的核心素养
导航 素养·目标定位 目 标 素 养 1.了解椭圆的实际背景,结合具体实际情景,理解并掌握椭 圆的定义,能够运用椭圆的定义解决问题. 2.掌握椭圆的标准方程,能根据条件求椭圆的标准方程. 3.掌握用相关点法求动点轨迹方程的方法. 4.通过学习,提升直观想象和数学抽象的核心素养
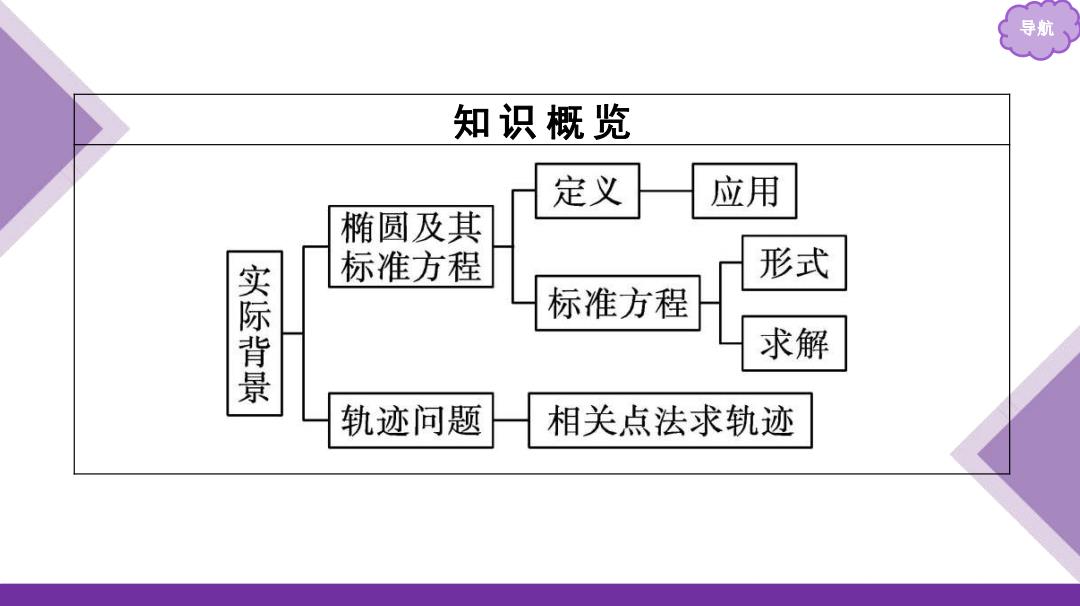
导航 知识概览 定义 应用 椭圆及其 标准方程 形式 实际背景 标准方程 求解 轨迹问题 相关点法求轨迹
导航 知 识 概 览

导航 课前·基础认知 1.椭圆的定义 平面内与两个定点F,F,的距离的 等于常数(大于 )的点的轨迹叫做椭圆这两个定点叫做椭圆的 ,两焦点间的距离叫做椭圆的 ,焦距的一半 称为
导航 课前·基础认知 1.椭圆的定义 平面内与两个定点F1 ,F2的距离的 和 等于常数(大于 |F1F2 | )的点的轨迹叫做椭圆.这两个定点叫做椭圆的 焦点 ,两焦点间的距离叫做椭圆的 焦距 ,焦距的一半 称为 半焦距

导航 微解读椭圆的定义中为什么要求常数要大于FF?如果常 数等于FF,那么动点的轨迹是什么图形? 提示:由椭圆的形状结合三角形中两边之和大于第三边可知 常数必须要大于FF;若常数等于FF,则动点的轨迹是线 段FFx
导航 微解读 椭圆的定义中为什么要求常数要大于|F1F2 |?如果常 数等于|F1F2 |,那么动点的轨迹是什么图形? 提示:由椭圆的形状结合三角形中两边之和大于第三边可知 常数必须要大于|F1F2 |;若常数等于|F1F2 |,则动点的轨迹是线 段F1F2
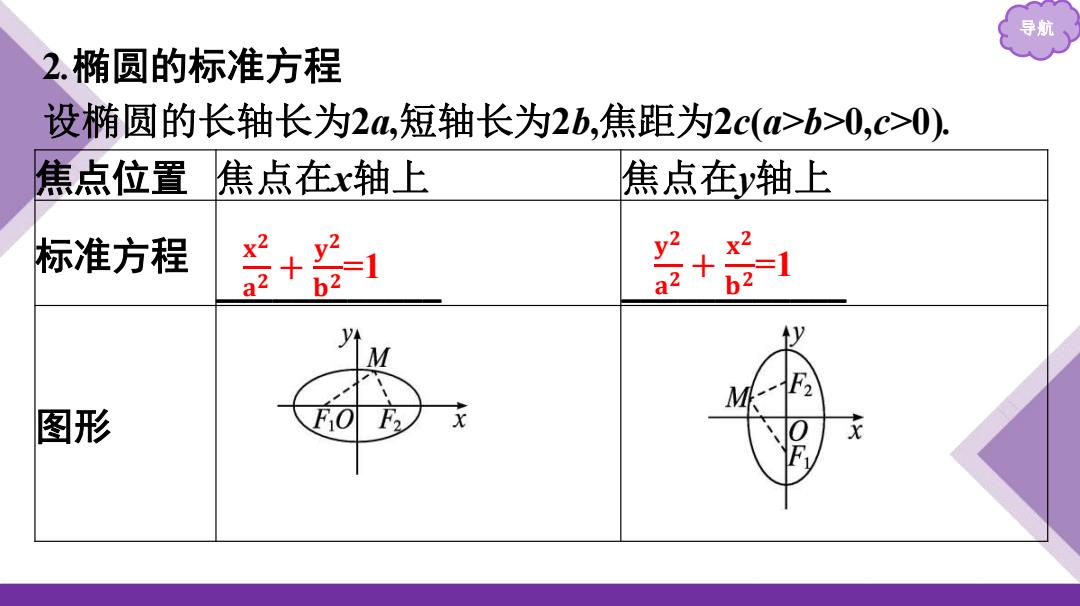
导航 2.椭圆的标准方程 设椭圆的长轴长为24,短轴长为2b,焦距为2c(>b>0,c>0) 焦点位置, 焦点在x轴上 焦点在y轴上 标准方程 +品 + 21 M 图形 1
导航 2.椭圆的标准方程 设椭圆的长轴长为2a,短轴长为2b,焦距为2c(a>b>0,c>0). 焦点位置 焦点在x轴上 焦点在y轴上 标准方程 ____________ ____________ 图形 𝐱 𝟐 𝐚 𝟐 + 𝐲 𝟐 𝐛 𝟐 =1 𝐲 𝟐 𝐚 𝟐 + 𝐱 𝟐 𝐛 𝟐 =1

导航、 焦点坐标 m,b,c的关系
导航 焦点坐标 F1 (-c,0),F2 (c,0) F1 (0,-c),F2 (0,c) a,b,c的关系 a 2=b2+c2

微探究方程 之+=1心0,>0一定表示椭圆吗?怎样根据 m n 椭圆方程判断其焦点所在的坐标轴? 提示:不一定,椭圆方程中,等式左边两个分母的值不能相等, 否则方程将表示圆。 判断该方程所表示的椭圆的焦点位置的方法:椭圆的焦点在X 轴上台标准方程中x项的分母较大;椭圆的焦点在y轴上台标 准方程中y2项的分母较大,即“焦点位置看大小,焦点随着大的 跑
导航 微探究 方程 =1(m>0,n>0)一定表示椭圆吗?怎样根据 椭圆方程判断其焦点所在的坐标轴? 提示:不一定,椭圆方程中,等式左边两个分母的值不能相等, 否则方程将表示圆. 判断该方程所表示的椭圆的焦点位置的方法:椭圆的焦点在x 轴上⇔标准方程中x 2项的分母较大;椭圆的焦点在y轴上⇔标 准方程中y 2项的分母较大,即“焦点位置看大小,焦点随着大的 跑” . 𝒙 𝟐 𝒎 + 𝒚 𝟐 𝒏

导航 课堂·重难突破 椭圆标准方程的理解 典例剖析 <5”是“方程X+y2表示椭圆”的(B m-1 5-m A.充分不必要条件 B.必要不充分条件 C充要条件 D.既不充分也不必要条件
导航 课堂·重难突破 一 椭圆标准方程的理解 典例剖析 1.“1<m<5”是“方程 𝒙 𝟐 𝒎-𝟏 + 𝒚 𝟐 𝟓-𝒎 =2 表示椭圆”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 B