
全程设计 第1课时 平面与平面垂直的判定定理
第1课时 平面与平面垂直的判定定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
导航 课前·基础认知 1.二面角的概念 ()定义:从一条直线出发的 所组成的图形 (2)相关概念:①这条直线叫做二面角的 ,②两个半平 面叫做
导航 课前·基础认知 1.二面角的概念 (1)定义:从一条直线出发的 两个半平面 所组成的图形. (2)相关概念:①这条直线叫做二面角的 棱 ,②两个半平 面叫做 二面角的面
(3)画法: B 导航 B 。P (4)记法:二面角a-l-或a-AB-B或P-1-Q或P-AB-2 (⑤)二面角的平面角:若有①O∈L;②OAca,OBcf;③ OA⊥l,OB⊥1,则二面角a--B的平面角是 B B (⑥)平面角是直角的二面角叫做 ,二面角的平面角a 的取值范围是
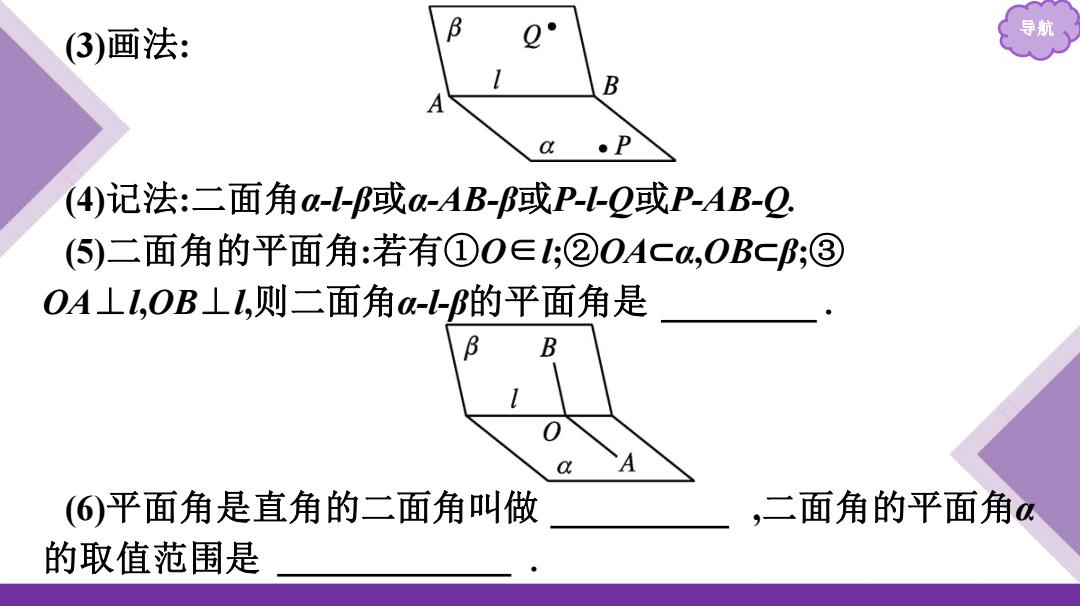
导航 (3)画法: (4)记法:二面角α-l-β或α-AB-β或P-l-Q或P-AB-Q. (5)二面角的平面角:若有①O∈l;②OA⊂α,OB⊂β;③ OA⊥l,OB⊥l,则二面角α-l-β的平面角是 ∠AOB . (6)平面角是直角的二面角叫做 直二面角 ,二面角的平面角α 的取值范围是 0°≤α≤180°
微思考1二面角的平面角的大小,是否与角的顶点在棱上 的位置有关? 提示:无关如图,OA∥O'A',OB∥O'B',根据等角定理可 知,∠AOB=∠A'O'B',即二面角的平面角的大小与角的顶点的 位置无关,只与二面角的大小有关 B
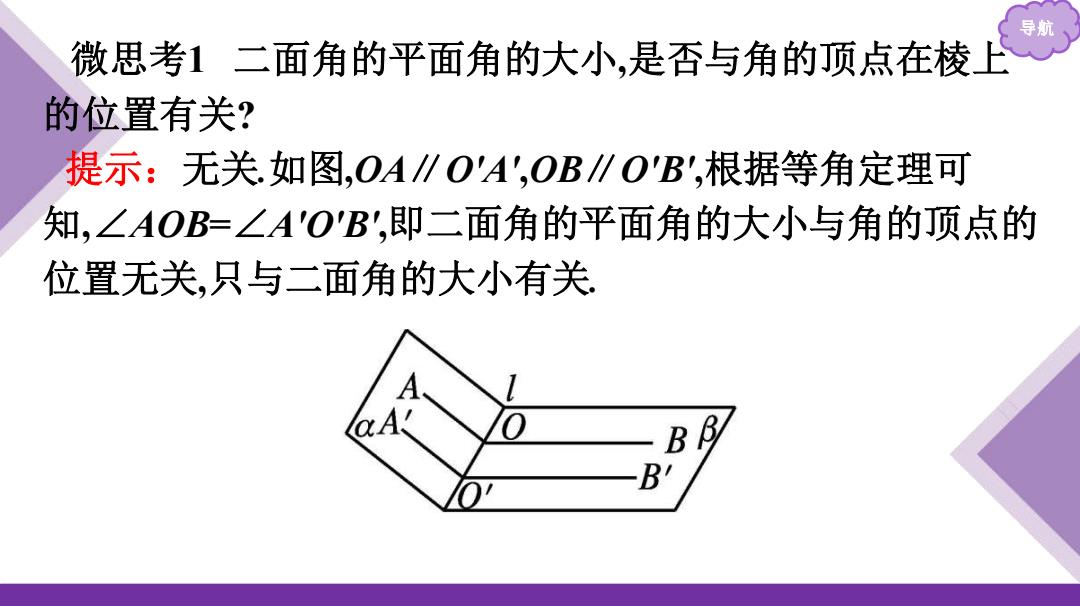
导航 微思考1 二面角的平面角的大小,是否与角的顶点在棱上 的位置有关? 提示:无关.如图,OA∥O'A',OB∥O'B',根据等角定理可 知,∠AOB=∠A'O'B',即二面角的平面角的大小与角的顶点的 位置无关,只与二面角的大小有关
导航 微探究如何求二面角大小? 提示:求二面角大小的步骤 作 作出平面角 证 证明所作的角满足定义,即为所求 二面角的平面角 将作出的角放在三角形中,计算出 平面角的大小 简称为“一作、二证、三求
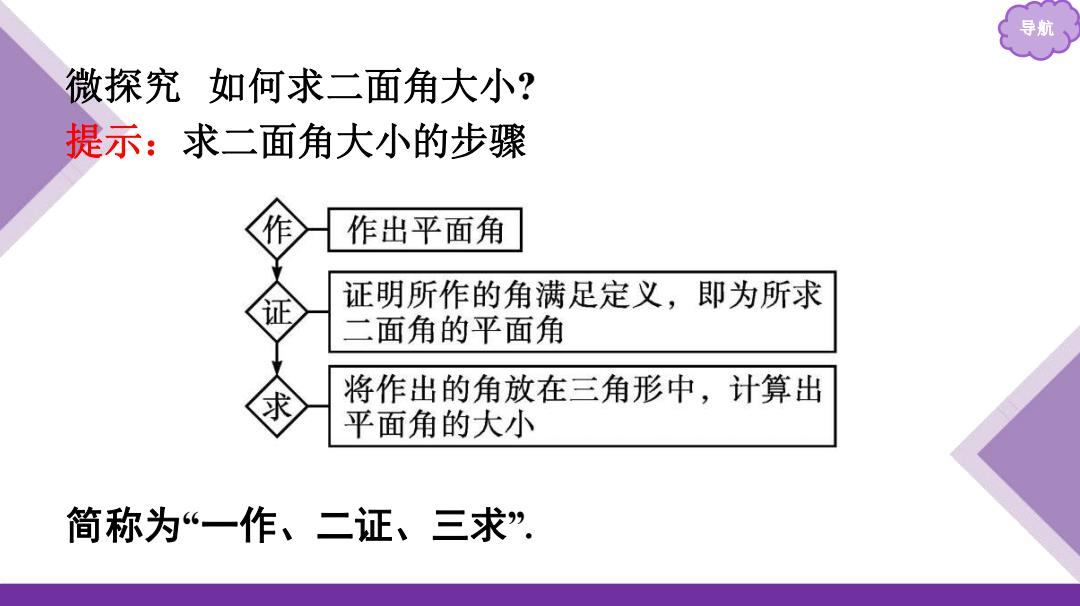
导航 微探究 如何求二面角大小? 提示:求二面角大小的步骤 简称为“一作、二证、三求”
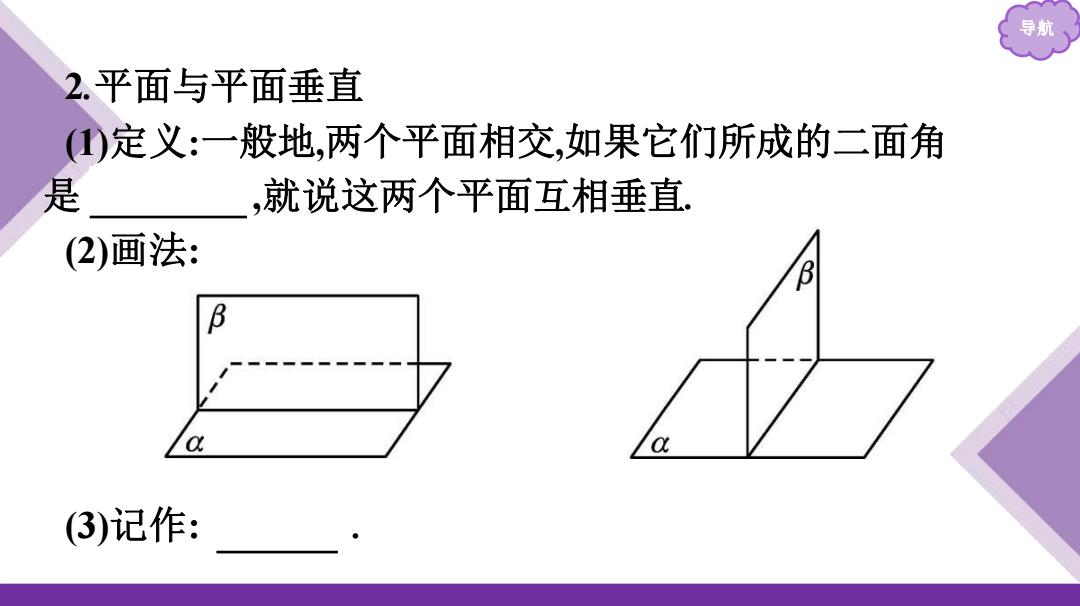
导航 2.平面与平面垂直 ()定义:一般地,两个平面相交,如果它们所成的二面角 是 ,就说这两个平面互相垂直. (2)画法: B a (3)记作:
导航 2.平面与平面垂直 (1)定义:一般地,两个平面相交,如果它们所成的二面角 是 直二面角,就说这两个平面互相垂直. (2)画法: (3)记作: α⊥β
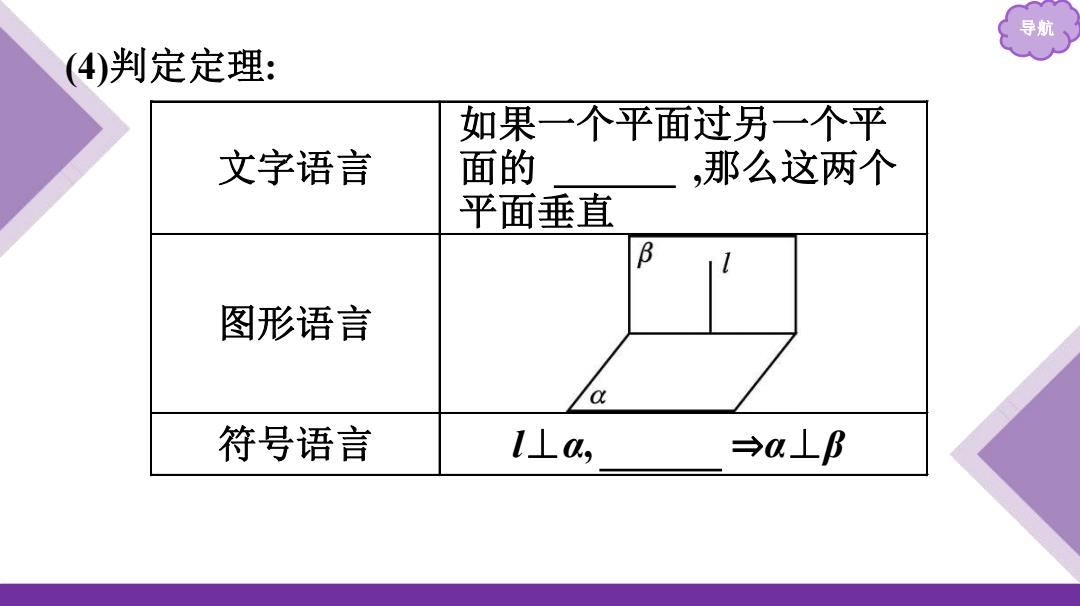
导航 4)判定定理: 如果一个平面过另一个平 文字语言 面的 ,那么这两个 平面垂直 B 图形语言 符号语言 L⊥a, →a⊥B
导航 (4)判定定理: 文字语言 如果一个平面过另一个平 面的 垂线 ,那么这两个 平面垂直 图形语言 符号语言 l⊥ α, l⊂β ⇒ α ⊥ β

导航 微思考2两个平面垂直,则一个平面内的任何一条直线都 垂直于另一个平面吗? 提示:不一定,只有在一个平面内垂直于交线的直线才垂直 于另一个平面
导航 微思考2 两个平面垂直,则一个平面内的任何一条直线都 垂直于另一个平面吗? 提示:不一定,只有在一个平面内垂直于交线的直线才垂直 于另一个平面
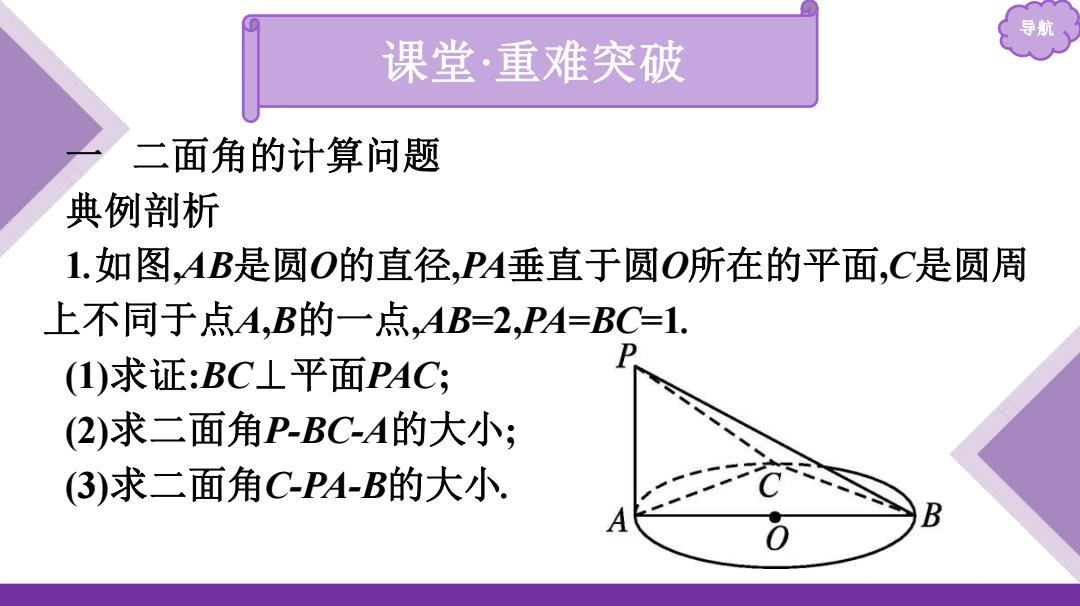
导航 课堂·重难突破 二面角的计算问题 典例剖析 1.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周 上不同于点A,B的一点,AB=2,PA=BC=1. (1)求证:BC⊥平面PAC; (2)求二面角P-BCA的大小; 3)求二面角C-PA-B的大小. B
导航 课堂·重难突破 一 二面角的计算问题 典例剖析 1.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周 上不同于点A,B的一点,AB=2,PA=BC=1. (1)求证:BC⊥平面PAC; (2)求二面角P-BC-A的大小; (3)求二面角C-PA-B的大小