
全程设计 8.3.1 棱柱、棱锥、棱台的表面积 和体积
8.3.1 棱柱、棱锥、棱台的表面积 和体积

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.棱柱、棱锥、棱台的表面积 多面体的表面积就是围成多面体各个面的面积的和. 微提醒棱柱、棱锥、棱台的表面积分别是它们侧面展开 图和底面的面积之和,因此弄清侧面展开图和底面的形状及 图中各线段的长,是解决与表面积有关问题的关键!
导航 课前·基础认知 1.棱柱、棱锥、棱台的表面积 多面体的表面积就是围成多面体各个面的面积的和. 微提醒 棱柱、棱锥、棱台的表面积分别是它们侧面展开 图和底面的面积之和,因此弄清侧面展开图和底面的形状及 图中各线段的长,是解决与表面积有关问题的关键

导期 2.棱柱、棱锥、棱台的体积 棱柱的体积公式:=S(底面面积为S,高为h); 棱锥的体积公式:=3Sh(底面面积为S,高为h); 棱台的体积公式:=hS+VSS+S.其中,S',S分别为棱台的 上、下底面面积,h为棱台的高. 微思考简单组合体分割成几个几何体,其表面积不变吗? 其体积呢? 提示:表面积变大,体积不变
导航 2.棱柱、棱锥、棱台的体积 棱柱的体积公式:V=Sh(底面面积为S,高为h); 棱锥的体积公式:V= Sh(底面面积为S,高为h); 棱台的体积公式:V= h(S'+ +S).其中,S',S分别为棱台的 上、下底面面积,h为棱台的高. 微思考 简单组合体分割成几个几何体,其表面积不变吗? 其体积呢? 提示:表面积变大,体积不变. 𝑺'𝑺 𝟏 𝟑 𝟏 𝟑
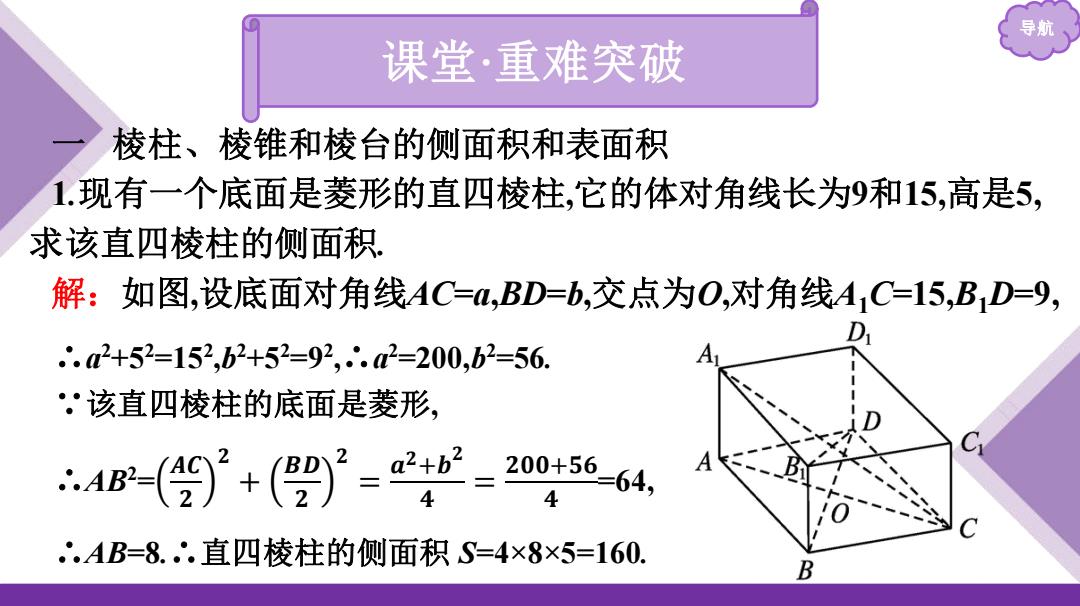
导 课堂·重难突破 棱柱、棱锥和棱台的侧面积和表面积 1.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5, 求该直四棱柱的侧面积 解:如图,设底面对角线AC=,BD=b,交点为O,对角线A1C=15,B1D=9, ∴.a2+52=152,b2+52=92,∴.a2=200,b2=56. ·该直四棱柱的底面是菱形, ∴(9+(- 200+56-64, 4 .AB=8..直四棱柱的侧面积S=4×8×5=160. B
导航 课堂·重难突破 一 棱柱、棱锥和棱台的侧面积和表面积 1.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5, 求该直四棱柱的侧面积. 解:如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9, ∴a 2 +5 2 =152 ,b 2 +5 2 =9 2 ,∴a 2 =200,b 2 =56. ∵该直四棱柱的底面是菱形, ∴AB2 = 𝑨𝑪 𝟐 𝟐 + 𝑩𝑫 𝟐 𝟐 = 𝒂 𝟐 +𝒃 𝟐 𝟒 = 𝟐𝟎𝟎+𝟓𝟔 𝟒 =64, ∴AB=8.∴直四棱柱的侧面积 S=4×8×5=160

导航 规律总结求几何体的表面积问题,通常将所给几何体分成 几个基本几何体,再通过这些基本几何体的表面积进行求和 或作差,从而获得几何体的表面积有时需将几何体展开,求其 展开图的面积,进而求得表面积
导航 规律总结 求几何体的表面积问题,通常将所给几何体分成 几个基本几何体,再通过这些基本几何体的表面积进行求和 或作差,从而获得几何体的表面积.有时需将几何体展开,求其 展开图的面积,进而求得表面积
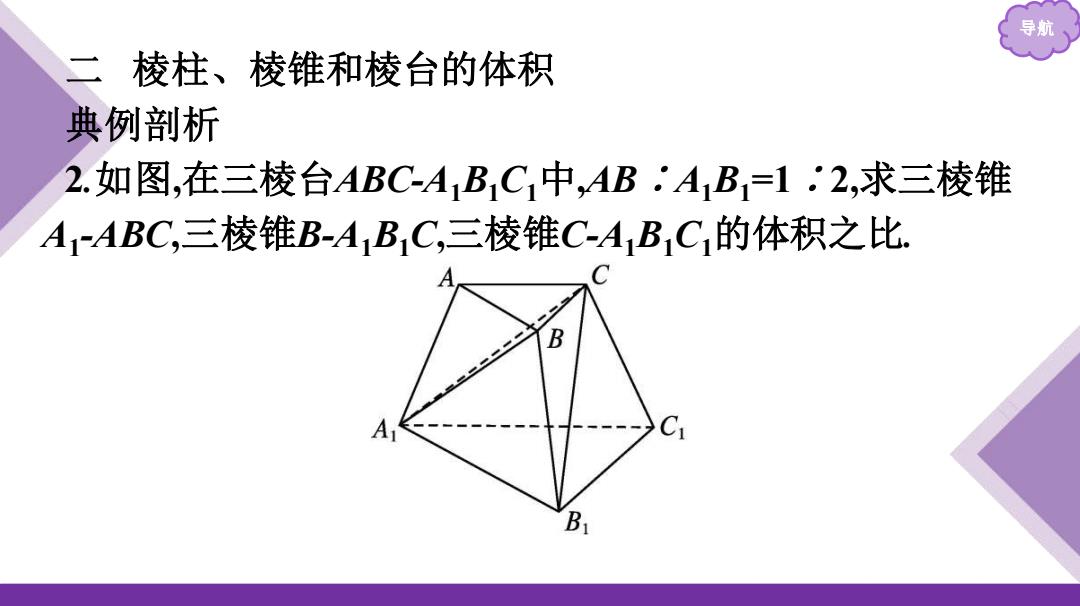
导航 二棱柱、棱锥和棱台的体积 典例剖析 2.如图,在三棱台ABC-A1B1C1中,AB,A1B=1·2,求三棱锥 A1ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比. C B
导航 二 棱柱、棱锥和棱台的体积 典例剖析 2.如图,在三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,求三棱锥 A1 -ABC,三棱锥B-A1B1C,三棱锥C-A1B1C1的体积之比

导航 解:设三棱台的高为h,S△4Bc=S, SAAaB1C:-4S.VAr-ARG =SAARC-h-Sh VcA181G1=3SaA1B1G1h等h.又V3S+4S+2S子S%, Vn.Aume-Va-VA-ARe-VcAumc-Sh-Sh-Sh-Sh 4 .三棱锥A1-ABC,B-A1B1C与CA1B1C1的体积比为1:2:4
导航 解:设三棱台的高为 h,S△ABC=S, 则𝑺△𝑨𝟏 𝑩𝟏 𝑪𝟏 =4S.∴𝑽𝑨𝟏-𝑨𝑩𝑪 = 𝟏 𝟑 S△ABC·h= 𝟏 𝟑 Sh, 𝑽𝑪-𝑨𝟏 𝑩𝟏 𝑪𝟏 = 𝟏 𝟑 𝑺△𝑨𝟏 𝑩𝟏 𝑪𝟏 ·h= 𝟒 𝟑 Sh.又 V 台= 𝟏 𝟑 h(S+4S+2S)= 𝟕 𝟑 Sh, ∴𝑽𝑩-𝑨𝟏 𝑩𝟏 𝑪 =V 台-𝑽𝑨𝟏-𝑨𝑩𝑪-𝑽𝑪-𝑨𝟏 𝑩𝟏 𝑪𝟏 = 𝟕 𝟑 Sh- 𝟏 𝟑 Sh- 𝟒 𝟑 Sh= 𝟐 𝟑 Sh, ∴三棱锥 A1-ABC,B-A1B1C 与 C-A1B1C1的体积比为 1∶2∶4
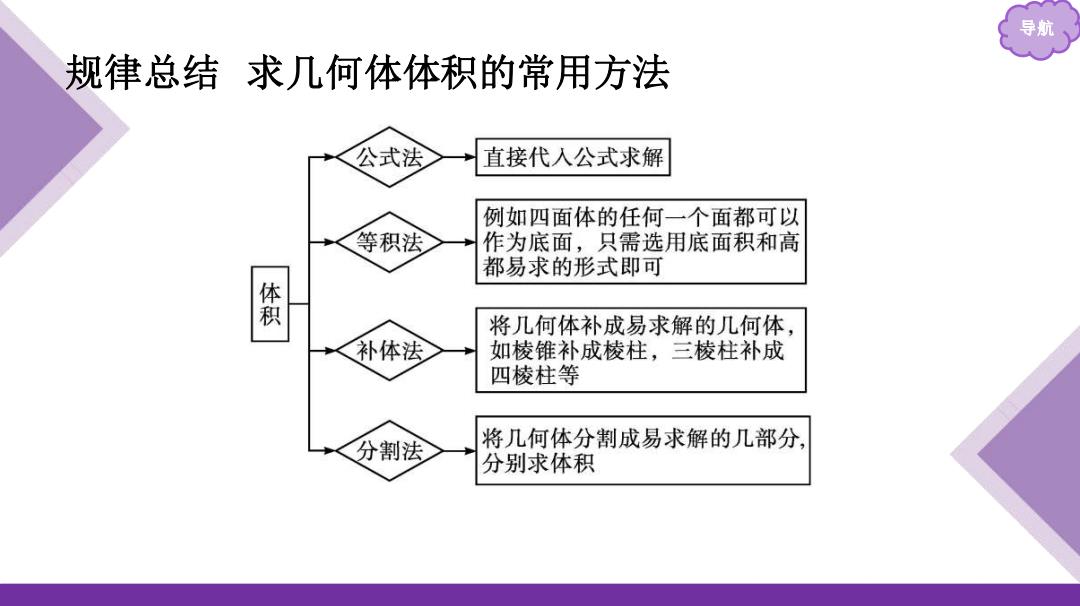
导航 规律总结求几何体体积的常用方法 公式法 直接代人公式求解 例如四面体的任何一个面都可以 等积法 作为底面,只需选用底面积和高 都易求的形式即可 賽 将几何体补成易求解的几何体, 补体法 如棱锥补成棱柱,三棱柱补成 四棱柱等 分割法 将几何体分割成易求解的几部分」 分别求体积
导航 规律总结 求几何体体积的常用方法

导 三棱台与棱锥之间关系的综合问题 典例剖析 3.已知正四棱台(上、下底是正方形,上底面的中心在下底面 的投影是下底面中心)上底面边长为6,高和下底面边长都是 12,求它的侧面积 解:如图,E,E1分别是BC,B1C1的中点, 0,O1分别是下、上底面正方形的中心
导航 三 棱台与棱锥之间关系的综合问题 典例剖析 3.已知正四棱台(上、下底是正方形,上底面的中心在下底面 的投影是下底面中心)上底面边长为6,高和下底面边长都是 12,求它的侧面积. 解:如图,E,E1分别是BC,B1C1的中点, O,O1分别是下、上底面正方形的中心