
全程设计 6.3.1 平面向量基本定理
6.3.1 平面向量基本定理

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1.平面向量基本定理 条件 e1,e2是同一平面内的两个 结 对于这一平面内的任一向量4,有且只有一对实数1,2, 论 使=
导航 课前·基础认知 1.平面向量基本定理 条 件 e1,e2是同一平面内的两个 不共线向量 结 论 对于这一平面内的任一向量 a,有且只有一对实数 λ1,λ2, 使 a= λ1e1+λ2e2

导航 2.基底 若e1,e2不共线,我们把{e1,e2}叫做表示这一平面内所有向量 的一个基底 微思考0能与另外一个向量构成基底吗? 提示:不能.基向量是不共线的,而0与任意向量都共线
导航 2.基底 若e1 ,e2不共线,我们把{e1 ,e2 }叫做表示这一平面内所有向量 的一个基底. 微思考 0能与另外一个向量a构成基底吗? 提示:不能.基向量是不共线的,而0与任意向量都共线

导航 课堂·重难突破 对基底概念的理解 典例剖析 1.设e1,e2是平面内所有向量的一个基底,则下列四组向量中, 不能作为基底的是(B) A.e1+e2和e1-e2 B.3e1-4e2和6e1-8e2 C.e1+2e2和2e+e2 D.e和e+e2
导航 课堂·重难突破 一 对基底概念的理解 典例剖析 1.设e1 ,e2是平面内所有向量的一个基底,则下列四组向量中, 不能作为基底的是( ) A.e1+e2和e1 -e2 B.3e1 -4e2和6e1 -8e2 C.e1+2e2和2e1+e2 D.e1和e1+e2 B

导航 解析:在选项B中, .6e1-8e2=23e1-4e2), ∴.6e1-8e2与3e1-4e共线, '.不能作为基底;选项A,C,D中两向量均不共线,可以作为基 底.故选B. 规律总结两个向量能否作为一个基底,关键是看这两个向 量是否共线.若共线,则不能作基底,反之,则可作基底
导航 解析:在选项B中, ∵6e1 -8e2 =2(3e1 -4e2 ), ∴6e1 -8e2与3e1 -4e2共线, ∴不能作为基底;选项A,C,D中两向量均不共线,可以作为基 底.故选B. 规律总结 两个向量能否作为一个基底,关键是看这两个向 量是否共线.若共线,则不能作基底,反之,则可作基底

导 二用基底表示向量 典例剖析 2.(1)如图,已知0A=m,0B=b,C为线段AO上距点A较近的一 个三等分点,D为线段CB上距点C较近的一个三等分点,则用 4,b表示0D= 答案:r+ 解析:0D=0B+BD=0B+BC -0B+(OC-OB)10B+30C0B+0A ab
导航 二 用基底表示向量 典例剖析 2.(1)如图,已知 =a, =b,C为线段AO上距点A较近的一 个三等分点,D为线段CB上距点C较近的一个三等分点,则用 a,b表示 = . 𝑶 𝑨 𝑶 𝑩 𝑶 𝑫 答案:𝟒 𝟗 a+ 𝟏 𝟑 b 解析:𝑶 𝑫 =𝑶 𝑩 + 𝑩 𝑫 =𝑶 𝑩 + 𝟐 𝟑 𝑩 𝑪 =𝑶 𝑩 + 𝟐 𝟑 (𝑶 𝑪 -𝑶 𝑩 )= 𝟏 𝟑 𝑶 𝑩 + 𝟐 𝟑 𝑶 𝑪 = 𝟏 𝟑 𝑶 𝑩 + 𝟐 𝟑 × 𝟐 𝟑 𝑶 𝑨 = 𝟒 𝟗 a+ 𝟏 𝟑 b

导 (2)如图,ABCD的对角线AC和BD交于点M,AB=,AD=b, 试用基底{a,b}表示MC,MA,MB. 解:AC=AB+AD=+b,BD=AD-AB=b-a A 因为平行四边形的对角线互相平分,所以MC号AC+动 MA=M元-0b因为而8丽-b2所以M压-MD-r头
导航 (2)如图,▱ABCD 的对角线 AC 和 BD 交于点 M,𝑨 𝑩 =a, 𝑨 𝑫 =b, 试用基底{a,b}表示𝑴 𝑪 ,𝑴 𝑨 ,𝑴 𝑩 . 解:𝑨 𝑪 =𝑨 𝑩 + 𝑨 𝑫 =a+b,𝑩 𝑫 = 𝑨 𝑫 -𝑨 𝑩 =b-a. 因为平行四边形的对角线互相平分,所以𝑴 𝑪 = 𝟏 𝟐 𝑨 𝑪 = 𝟏 𝟐 a+ 𝟏 𝟐 b. 𝑴 𝑨 =-𝑴 𝑪 =- 𝟏 𝟐 a- 𝟏 𝟐 b.因为 𝑴 𝑫 = 𝟏 𝟐 𝑩 𝑫 = 𝟏 𝟐 b- 𝟏 𝟐 a,所以𝑴 𝑩 =- 𝑴 𝑫 = 𝟏 𝟐 a- 𝟏 𝟐 b

导航 规律总结平面向量基本定理的作用以及注意点 ()根据平面向量基本定理,用基底表示向量,实质上是利用 三角形法则或平行四边形法则,进行向量的加减法运算. (2)要注意适当选择向量所在的三角形或平行四边形,利用已 知向量表示未知向量,或找到已知向量与未知向量的关系,用 方程的观点求出未知向量
导航 规律总结 平面向量基本定理的作用以及注意点 (1)根据平面向量基本定理,用基底表示向量,实质上是利用 三角形法则或平行四边形法则,进行向量的加减法运算. (2)要注意适当选择向量所在的三角形或平行四边形,利用已 知向量表示未知向量,或找到已知向量与未知向量的关系,用 方程的观点求出未知向量
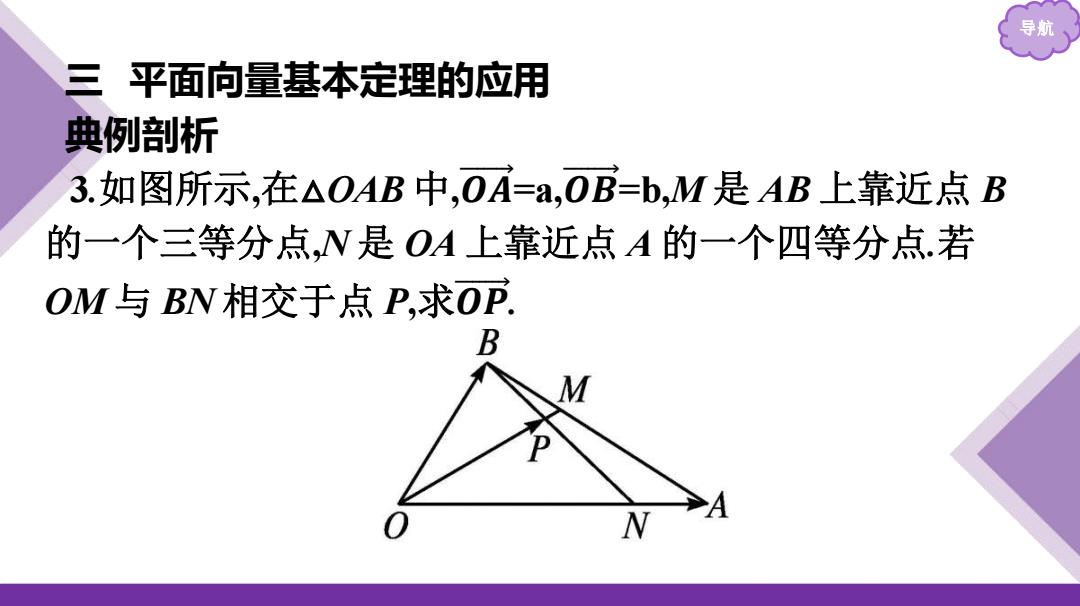
导航 三平面向量基本定理的应用 典例剖析 3.如图所示,在△OAB中,OA=A,OB=b,M是AB上靠近点B 的一个三等分点,N是OA上靠近点A的一个四等分点.若 OM与BN相交于点P,求OP. B M N
导航 三 平面向量基本定理的应用 典例剖析 3.如图所示,在 △OAB 中,𝑶 𝑨 = a,𝑶 𝑩 = b,M 是 AB 上靠近点 B 的一个三等分点,N 是 OA 上靠近点 A 的一个四等分点.若 OM 与 BN 相交于点 P,求 𝑶 𝑷