
全程设计 第四章 指数丞数与对数函数 4.5 函数的应用(二) 4.5.1 函数的零点与方程的解
第四章 指数函数与对数函数 4.5 函数的应用(二) 4.5.1 函数的零点与方程的解

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
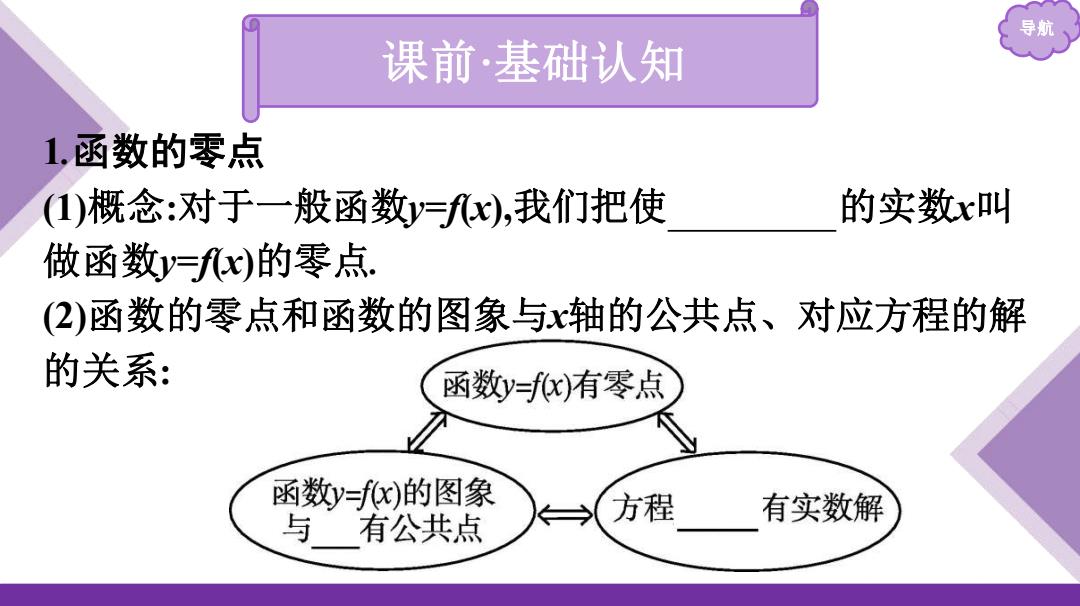
导航 课前·基础认知 1,函数的零点 (1)概念:对于一般函数y=fx),我们把使 的实数x叫 做函数y=f)的零点 (2)函数的零点和函数的图象与x轴的公共点、对应方程的解 的关系: 函数y=fx)有零点 函数y=x)的图象 与有公共点 →(方程 有实数解
导航 课前·基础认知 1.函数的零点 (1)概念:对于一般函数y=f(x),我们把使 f(x)=0 的实数x叫 做函数y=f(x)的零点. (2)函数的零点和函数的图象与x轴的公共点、对应方程的解 的关系:

导航 微点拨1(1)函数的零点不是一个点,而是一个实数,当自变量 取该实数时,函数值为零; (2)并不是任何函数都有零点,比如y=1y=x2+1等就没有零点; (3)若函数x)有零点,则零,点一定是定义域内的一个实数
导航 微点拨1 (1)函数的零点不是一个点,而是一个实数,当自变量 取该实数时,函数值为零; (2)并不是任何函数都有零点,比如y=1,y=x2+1等就没有零点; (3)若函数f(x)有零点,则零点一定是定义域内的一个实数
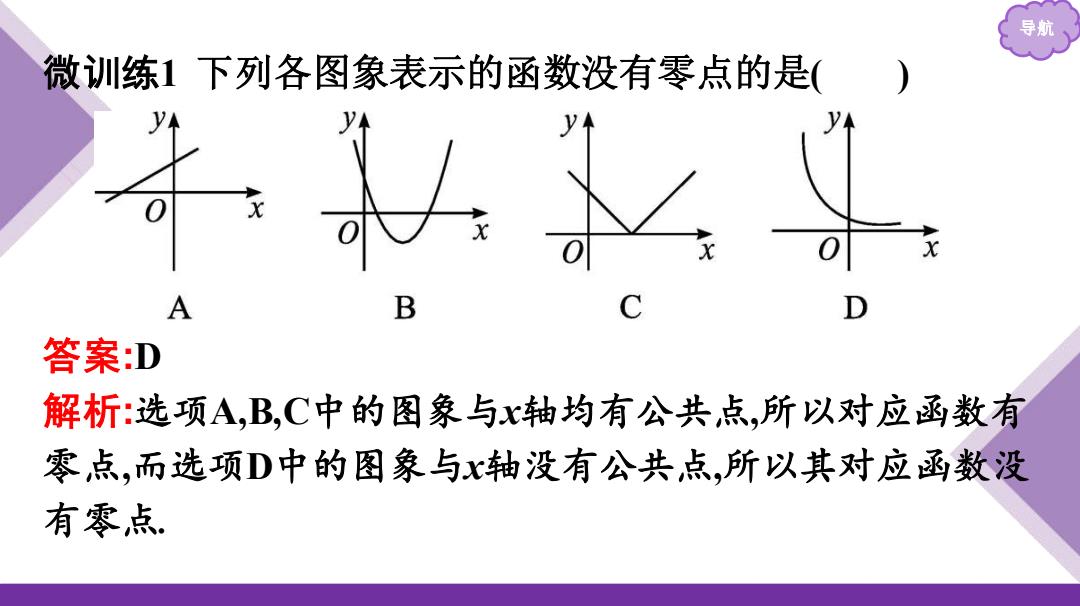
导期 微训练1下列各图象表示的函数没有零点的是( A B 答案:D 解析:选项A,B,C中的图象与x轴均有公共点,所以对应函数有 零点,而选项D中的图象与x轴没有公共点,所以其对应函数没 有零点
导航 微训练1 下列各图象表示的函数没有零点的是( ) 答案:D 解析:选项A,B,C中的图象与x轴均有公共点,所以对应函数有 零点,而选项D中的图象与x轴没有公共点,所以其对应函数没 有零点

导航 2.函数零点存在定理 ()条件:①函数y=fx)在区间[a,b上的图象是一条 的曲线;② (2)结论:函数y=fx)在区间(,b)内至少有一个零点,即存在 c∈(a,b),使得 ,这个c也就是方程fx)=O的解
导航 2.函数零点存在定理 (1)条件:①函数y=f(x)在区间[a,b]上的图象是一条 连续不断 的曲线;② f(a)f(b)<0 . (2)结论:函数y=f(x)在区间(a,b)内至少有一个零点,即存在 c∈(a,b),使得 f(c)=0 ,这个c也就是方程f(x)=0的解

导航 微点拨2(1)函数y=fx)在区间(a,b)内有零点,不一定有 @b)0. (2)函数零点存在定理不考虑闭区间[,b]的端点处,而是考虑 开区间(a,b)内有无零点问题,若fa)=0,或fb)=0,则M或b也是函 数零,点,但不是该定理研究的内容
导航 微点拨2 (1)函数y=f(x)在区间(a,b)内有零点,不一定有 f(a)f(b)0. (2)函数零点存在定理不考虑闭区间[a,b]的端点处,而是考虑 开区间(a,b)内有无零点问题,若f(a)=0,或f(b)=0,则a或b也是函 数零点,但不是该定理研究的内容

导期 微训练2若函数fx)的图象在R上连续不断,且满足 0)0,f2)>0,测下列说法正确的是( Ax)在区间0,1)内一定有零点,在区间(1,2)内一定没有零点 Bfx)在区间0,1)内一定没有零点,在区间(1,2)内一定有零点 Cx)在区间(0,1)内一定有零点,在区间(1,2)内可能有零点 Dfx)在区间(0,1)内可能有零点,在区间(1,2)内一定有零点
导航 微训练2 若函数f(x)的图象在R上连续不断,且满足 f(0)0,f(2)>0,则下列说法正确的是( ) A.f(x)在区间(0,1)内一定有零点,在区间(1,2)内一定没有零点 B.f(x)在区间(0,1)内一定没有零点,在区间(1,2)内一定有零点 C.f(x)在区间(0,1)内一定有零点,在区间(1,2)内可能有零点 D.f(x)在区间(0,1)内可能有零点,在区间(1,2)内一定有零点
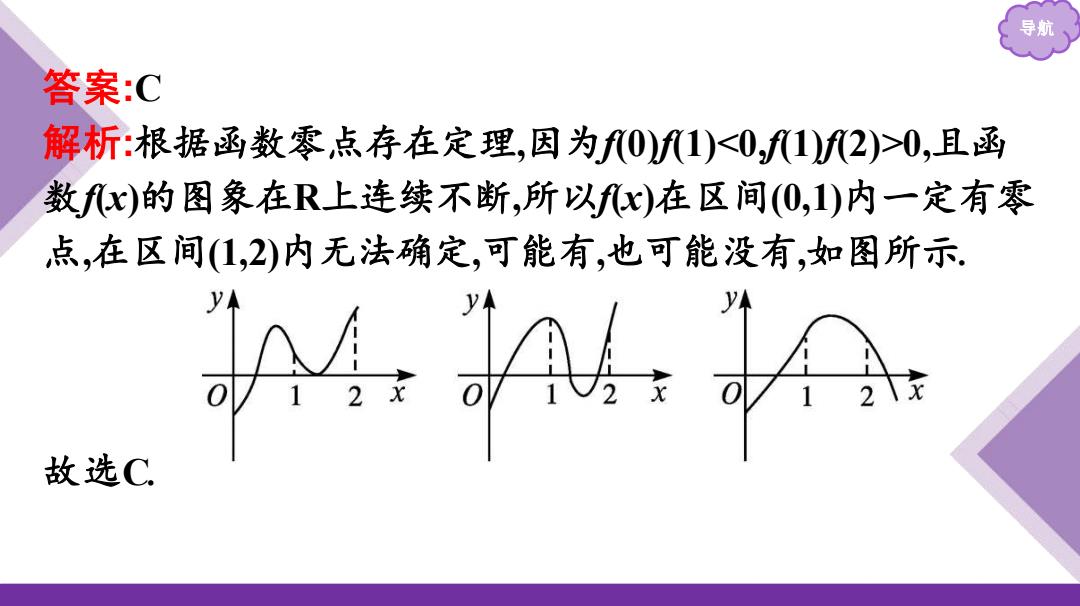
导 答案:C 解析:根据函数零点存在定理,因为f0)1)0,且函 数fx)的图象在R上连续不断,所以x)在区间(0,1)内一定有零 点,在区间(1,2)内无法确定,可能有,也可能没有,如图所示. 故选C
导航 答案:C 解析:根据函数零点存在定理,因为f(0)f(1)0,且函 数f(x)的图象在R上连续不断,所以f(x)在区间(0,1)内一定有零 点,在区间(1,2)内无法确定,可能有,也可能没有,如图所示. 故选C

导航 课堂·重难突破 函数零点的概念及求法 典例剖析 1.(1)函数fx)=(x2-1)√x24的零点是 (2)设函数fx)=21-x-4gx)=1-l0g2(c+3),则函数fx)的零点与g) 的零点之和为 (3)若关于x的方程x2-1=有两个不相等的实数解,则实数α的 取值范围是 答案:(1)2或-2(2)-2 (3){a=0或心>1}
导航 课堂·重难突破 一 函数零点的概念及求法 典例剖析 1.(1)函数f(x)=(x 2 -1)· 的零点是 . (2)设函数f(x)=2 1-x -4,g(x)=1-log2 (x+3),则函数f(x)的零点与g(x) 的零点之和为 . (3)若关于x的方程|x2 -1|=a有两个不相等的实数解,则实数a的 取值范围是 . 答案:(1)2或-2 (2)-2 (3){a|a=0或a>1} 𝒙 𝟐-𝟒