
全程设计 第四章 指数丞数与对数函数 4.1指数 第2课时 根式与分数指数幂的互化
第四章 指数函数与对数函数 4.1 指数 第2课时 根式与分数指数幂的互化

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破

导航 课前·基础认知 1分数指数幂 ()规定正数的正分数指数幂的意义是: a器=Vaa0,mn∈N,n>I)店 (2)规定正数的负分数指数幂的意义是: m 1 1 an=- =am(a>0,m,n∈N,>1); an (3)规定0的正分数指数幂等于,0的负分数指数幂
导航 课前·基础认知 1.分数指数幂 (1)规定正数的正分数指数幂的意义是: (2)规定正数的负分数指数幂的意义是: (3)规定0的正分数指数幂等于 0 ,0的负分数指数幂 没有意义 . 𝒂 𝒎 𝒏 = 𝒏 𝒂 𝒎(a>0,m,n∈N * ,n>1); 𝒂 - 𝒎 𝒏 = 𝟏 𝒂 𝒎 𝒏 = 𝟏 𝒏 𝒂 𝒎 (a>0,m,n∈N * ,n>1);

导航 2.有理数指数幂的运算性质 整数指数幂的运算性质,可以推广到有理数指数幂,即: (1)W'=H*(a>0,rS∈Q); (2)(m)=m*(>0,,S∈Q); 3)(ab)='br(>0,b>0,r∈Q)
导航 2.有理数指数幂的运算性质 整数指数幂的运算性质,可以推广到有理数指数幂,即: (1)a ra s=ar+s(a>0,r,s∈Q); (2)(a r ) s=ars(a>0,r,s∈Q); (3)(ab) r=arb r (a>0,b>0,r∈Q)

导航 微训练 (1)化简:814= 答案:27 (2)用根式或分数指数幂表示下列各式: ,a≥0.,点a 13 1 3 0 解a5=Va;a4=a(>0);Va=a3=a2; 泰-是ae0
导航 微训练 (1)化简:8 𝟏 𝟑𝟒 = . 答案 :27 (2)用根式或分数指数幂表示下列各式: 𝒂𝟏𝟓,𝒂𝟑𝟒(a>0), 𝐚𝟔 𝟑 , 𝟏 𝐚𝟑(a>0). 解:𝐚𝟏𝟓 = 𝒂𝟓 ;𝒂𝟑𝟒 = 𝒂𝟑 𝟒 (a>0); 𝒂𝟔 𝟑 = 𝒂𝟔𝟑=a 2; 𝟏 𝒂𝟑 = 𝟏𝒂𝟑𝟐 = 𝒂-𝟑𝟐(a>0)

导航 3.无理数指数幂 一般地,无理数指数幂“(>0,a为无理数)是一个确定的 .有理数指数幂的运算性质同样适用于无理数指数幂
导航 3.无理数指数幂 一般地,无理数指数幂a α (a>0,α为无理数)是一个确定的 实数 .有理数指数幂的运算性质同样适用于无理数指数幂

导航 课堂·重难突破 根式与分数指数幂的互化 典例剖析 1.用分数指数幂表示下列各式(心0,b>0): (1)a2Va;2)Wa√a; (3)Va2.Va3;(4)(a)2-Vab3
导航 课堂·重难突破 一 根式与分数指数幂的互化 典例剖析 1.用分数指数幂表示下列各式(a>0,b>0): (1)a 2 𝒂;(2) 𝒂 𝒂; (3) 𝒂𝟐 𝟑 · 𝒂𝟑;(4)( 𝒂 𝟑 ) 2 · 𝒂𝒃𝟑
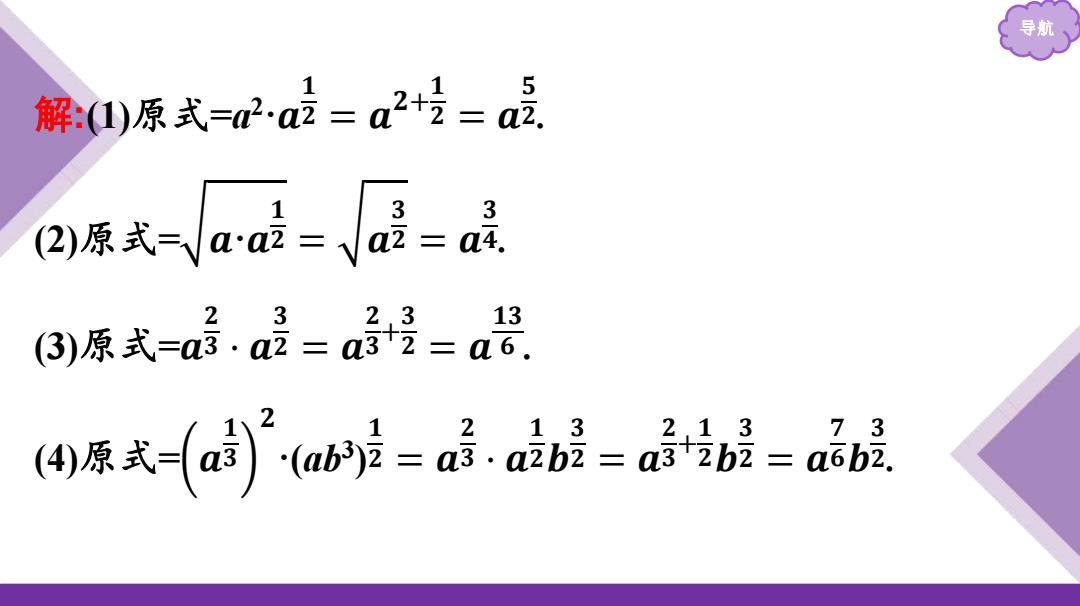
导航 解:原式=2a2=a2+号 u2. 日s-aai-0园 3 :a4. ③)原式=a品.品=+号 23 13 =a6, ④原式-(}aw过=b2 13 2,13 73 =a3 2b2 a6b2
导航 解:(1)原式=a2 ·𝒂 𝟏 𝟐 = 𝒂 𝟐+ 𝟏 𝟐 = 𝒂 𝟓 𝟐. (2)原式= 𝒂·𝒂 𝟏 𝟐 = 𝒂 𝟑 𝟐 = 𝒂 𝟑 𝟒. (3)原式=𝒂 𝟐 𝟑 ·𝒂 𝟑 𝟐 = 𝒂 𝟐 𝟑 + 𝟑 𝟐 = 𝒂 𝟏𝟑 𝟔 . (4)原式= 𝒂 𝟏 𝟑 𝟐 ·(ab3 ) 𝟏 𝟐 = 𝒂 𝟐 𝟑 ·𝒂 𝟏 𝟐𝒃 𝟑 𝟐 = 𝒂 𝟐 𝟑 + 𝟏 𝟐𝒃 𝟑 𝟐 = 𝒂 𝟕 𝟔𝒃 𝟑 𝟐

导期 规律总结 根式与分数指数幂互化的规律 (①)根指数化为分数指数的分母,被开方数(式)的指数化为 分数指数的分子 (2)在具体计算时,通常会把根式转化成分数指数幂的形式,然 后利用有理数指数幂的运算性质解题 (3)当根式为多重根式时,要清楚哪个是被开方数,一般由里向 外用分数指数幂依次写出
导航 根式与分数指数幂互化的规律 (1)根指数 化为 分数指数的分母,被开方数(式)的指数 分数指数的分子. (2)在具体计算时,通常会把根式转化成分数指数幂的形式,然 后利用有理数指数幂的运算性质解题. (3)当根式为多重根式时,要清楚哪个是被开方数,一般由里向 外用分数指数幂依次写出. 化为

二指数幂的运算 导航 典例剖析 2.计算下列各式: π3π (1)a4a4m(a>0); (2)2V3×V1.5×V12; 2 32写5ur24(2》3m+0 21 11 (43a3b4x(-8a2b 45a4.b3
导航 二 指数幂的运算 典例剖析 2.计算下列各式 : (1) 𝒂 𝛑𝟒 𝒂 𝟑 𝛑𝟒 a-π(a>0); (2)2 𝟑 × 𝟏.𝟓 𝟑 × 𝟏 𝟐 𝟔 ; (3) 𝟐 𝟕𝟗 𝟎.𝟓 + 0.1-2 + 𝟐 𝟏 𝟎 𝟐 𝟕 -𝟐𝟑-3 π 0 + 𝟑 𝟕 𝟒 𝟖; (4)(𝟑 𝒂 𝟐𝟑 𝒃 𝟏𝟒)×(-𝟖 𝒂 𝟏𝟐 𝒃 𝟏𝟐) -𝟒 𝒂𝟒 𝟔 · 𝒃𝟑