
全程设计 第五章 三角函数 5.4 三角国数的图象与性质 5.4.1 正弦函数、余弦函数的图象
第五章 三角函数 5.4 三角函数的图象与性质 5.4.1 正弦函数、余弦函数的图象

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
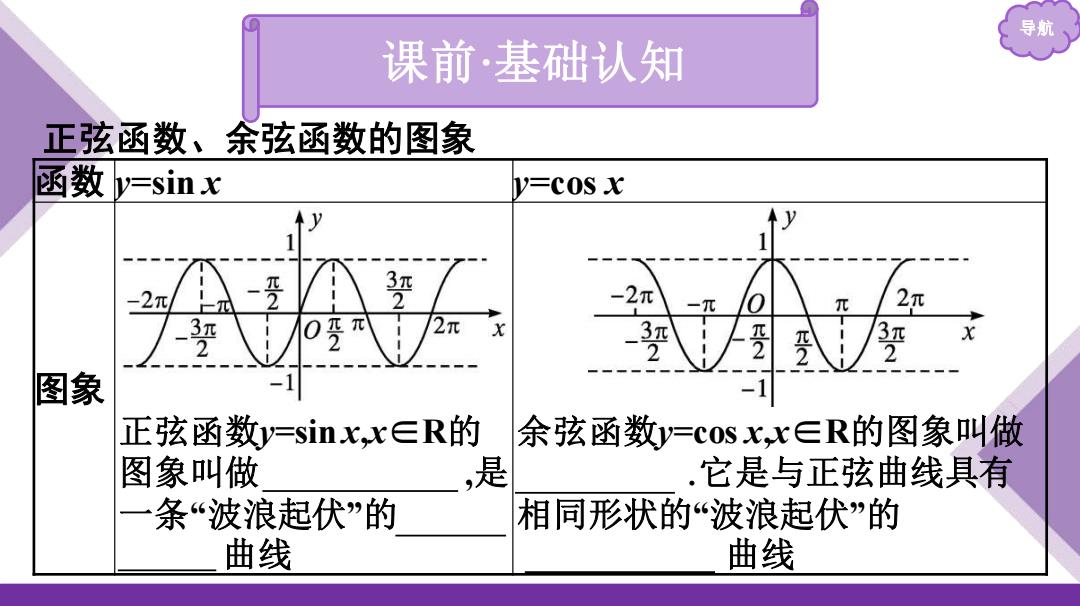
导航 课前·基础认知 正弦函数、余弦函数的图象 函数y=sinx V-cOS x y 3π -2π -2π 一兀 0 2π 3π 0 2π 3 2 3 图象 -1 -1 正弦函数y=sinx,x∈R的 余弦函数y=cosx,x∈R的图象叫做 图象叫做 ,是 ,它是与正弦曲线具有 一条“波浪起伏”的 相同形状的“波浪起伏”的 曲线 曲线
导航 课前·基础认知 正弦函数、余弦函数的图象 函数 y=sin x y=cos x 图象 正弦函数y=sin x,x∈R的 图象叫做 正弦曲线 ,是 一条“波浪起伏”的 连续 光滑 曲线 余弦函数y=cos x,x∈R的图象叫做 余弦曲线 .它是与正弦曲线具有 相同形状的“波浪起伏”的 连续光滑 曲线

导航、 函数 y=sin x v-cos x 图象 画法 “五点法” “五点法” 关键 (0,0), ,(元,0), (0,10, ,(π,-1), 五点 ,(2π,0) ,(2m,1)
导航 函数 y=sin x y=cos x 图象 画法 “五点法” “五点法” 关键 五点 (0,0), 𝛑 𝟐 ,𝟏 ,(π,0), 𝟑𝛑 𝟐 ,-𝟏 ,(2π,0) (0,1), 𝛑 𝟐 ,𝟎 ,(π,-1), 𝟑𝛑 𝟐 ,𝟎 ,(2π,1)

导航 微点拨五点法画图的优越性 ()避免了“描,点法”画图的烦琐,抓住了“描点法”的本质,使列 表更具有目标性,针对性。 (2)计算方便,描点准确. (3)由于抓住了关键点,所以更能准确反映图象全貌
导航 微点拨五点法画图的优越性 (1)避免了“描点法”画图的烦琐,抓住了“描点法”的本质,使列 表更具有目标性,针对性. (2)计算方便,描点准确. (3)由于抓住了关键点,所以更能准确反映图象全貌

微训练()已知正弦函数的图象过点(,m),则m的值为 D.1 (2)用五点作图法作y=1+c0sx,x∈0,2π的图象时,其中第二个 关键点的坐标为 答案:1)A(2)(,1) 解析:(0)根据题意,得si哈=2故选A 1
导航 微训练 (1)已知正弦函数的图象过点 𝛑 𝟔 ,𝒎 ,则 m 的值为 ( ) A. 𝟏 𝟐 B.- 𝟏 𝟐 C. 𝟑 𝟐 D.1 (2)用五点作图法作y=1+cos x,x∈[0,2π]的图象时,其中第二个 关键点的坐标为 . 答案:(1)A (2) 𝛑 𝟐 ,𝟏 解析:(1)根据题意,得 m=sin𝛑 𝟔 = 𝟏 𝟐 ,故选 A

导航 课堂·重难突破 “五点法”作图的应用 典例剖析 1.已知函数fx)=1+2sin七,用“五点法”作出函数y=fx)在区间 [0,2π上的图象
导航 课堂·重难突破 一 “五点法”作图的应用 典例剖析 1.已知函数f(x)=1+2sin x,用“五点法”作出函数y=f(x)在区间 [0,2π]上的图象

导航 解:列表如下: 3π X 0 π2 元 2元 2 432 sinx 0 1 0 -1 0 1 1+2sin x 3 1 -1 1 9 变 2元 描,点、连线即可得到函数y=fx)在区间[0,2π]上的图象,如图 所示
导航 解:列表如下: x 0 𝛑 𝟐 π 𝟑𝛑 𝟐 2π sin x 0 1 0 -1 0 1+2sin x 1 3 1 -1 1 描点、连线即可得到函数y=f(x)在区间[0,2π]上的图象,如图 所示

导航 规律总结 应用“五点法”作图的步骤 第一步:列表 令x取0受元,2,对应求出的值列出对应值表; 第二步:建系,描点 建立平面直角坐标系,从左至右依次将上述五点描出来; 第三步:连线 用平滑曲线从左到右依次连接各点,即可得到正弦(余弦)函数 在区间[0,2π上的图象
导航 应用“五点法”作图的步骤 第一步:列表 令x取 对应求出y的值列出对应值表; 第二步:建系,描点 建立平面直角坐标系,从左至右依次将上述五点描出来; 第三步:连线 用平滑曲线从左到右依次连接各点,即可得到正弦(余弦)函数 在区间[0,2π]上的图象. 0,𝛑 𝟐 ,π, 𝟑𝛑 𝟐 ,2π

导航 二 利用正弦函数、余弦函数的图象解不等式 典例剖析 2.(1)求函数-1-2 cosxlg(2sinx-1)的定义域; (2)求函数=36-x2+lgc0sx的定义域
导航 二 利用正弦函数、余弦函数的图象解不等式 典例剖析 2.(1)求函数 y= 𝟏-𝟐𝐜𝐨𝐬𝒙lg(2sin x-1)的定义域; (2)求函数 y= 𝟑𝟔-𝒙 𝟐 +lg cos x 的定义域